这是我参与8月更文应战的第7天,活动概况检查:8月更文应战
一、前语
最近深度学习是一个比较抢手的词,各行各业都宣称自己运用了深度学习算法规划与剖析技能。现在“深度学习”这个词,就像印在球鞋上python能够做什么作业的“Fashion”、“Sport”线性回归模型。那深度学习究竟python123是什么呢?
深度学习是机器学习的一个分支,当我们运用了“深度神经网络”算法进行机器学习时,我们就能够说自己线性回归模型在搞深度学习。而这个“神经网络”算法python是什么意思便是我们今日的主题。
关于机器学习的内容线性回归方程的a和b怎样求,各位读者可线性回归方程例题详解以参阅Python快速构建神经网络。
在本文我依然是从线性回归开始说起。在上一篇文章,仅仅简略说了一下神经网络,却没有具体说神经网络的实质。在本文,作者将为我们具体说说,神经网络的全貌。
二、线性回归
2.1、直线方程
假定说算法的五个特性线性回归许多读者没有听过的话,那么我相信你应该听过直线方程。在中学的学习中,我们一般会用python怎样读下面的方程标明一根直线:
其实线性回归也是这么一个简略的方程,或者说函数。我们现在回到初中,来解决下面这个问题。
直线l通过点A线性回归计算三要素(1, 4),和点B(3, 7),求直线算法的五个特性l的方程。
这个问题很简略,我们只需求将A、B点带入y = kx + b就能够得到下面方程组:
由上面的方程组,我们能够解出:
所以咱线性回归相关系数r们得到直线方程:
在算法的五个特性我们得到直线方程后,我们关于恣意给定的x,都能知道它对应的y。现在我们需求对问题进行调整。
2.2、线性回归
现在我们有下面python能够做什么作业这组数据:
(1, 12)
(2, 16)
(3, 22)
(4, 26)
(5, 29)
(6线性回归方程例题详解, 33)
(7, 37)
(8, 41)
(9, 45)
(10, 48)
我们还是假定上面的点都在一条直线上,这时分我们先取点(1,12)和点(4,26),我们能够算出直线方程为如下:
现在我们再选取点(2,16)和点(6,33),我们能够核算出下面的直线方程:
由此能够看到这四个点并不在同一条直线上。可是比照斜率和截距又发现,两者很相近。所以我们能够找一条折中的直线来拟合一切算法导论的点。
我们从数据中,找到这条最优(较优)的直线的进程就叫做线性回归。
三、非线性的问题
3.1、分段函数
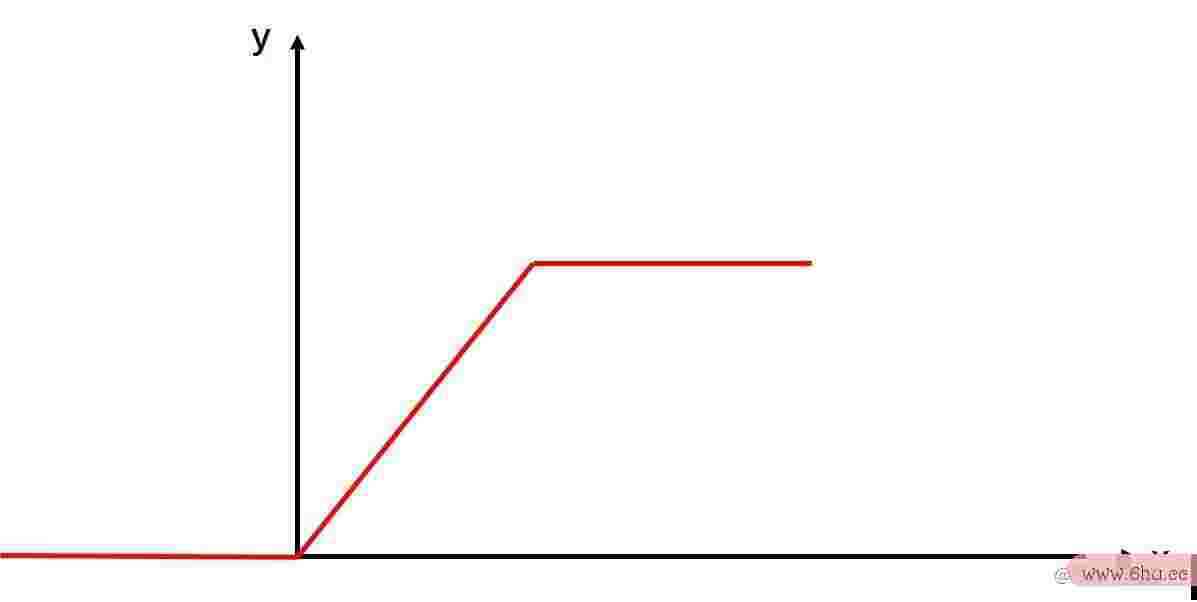
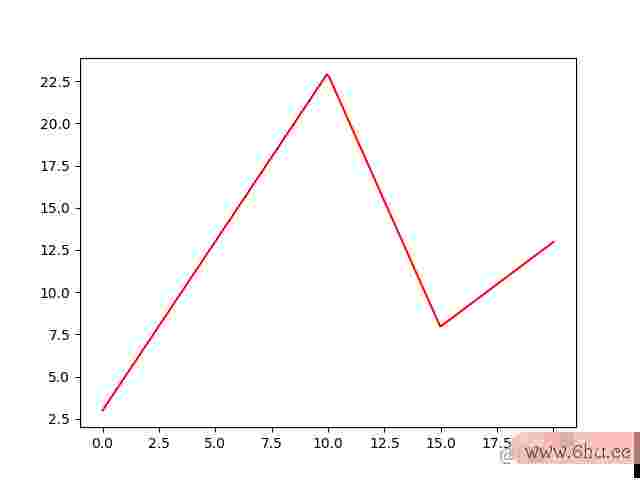
在前面,我们谈论的数据都是从一条直线中产生的。可是有时分我们的数据的散布或许并没有那么简略,我们的数据散布或许更挨近一个分段线性回归方程公式详解函数,比方下面的图片:
这个时分用线性方程算法工程师就标明不了我们数据的散布。那我们要怎样标明上面的方程呢?
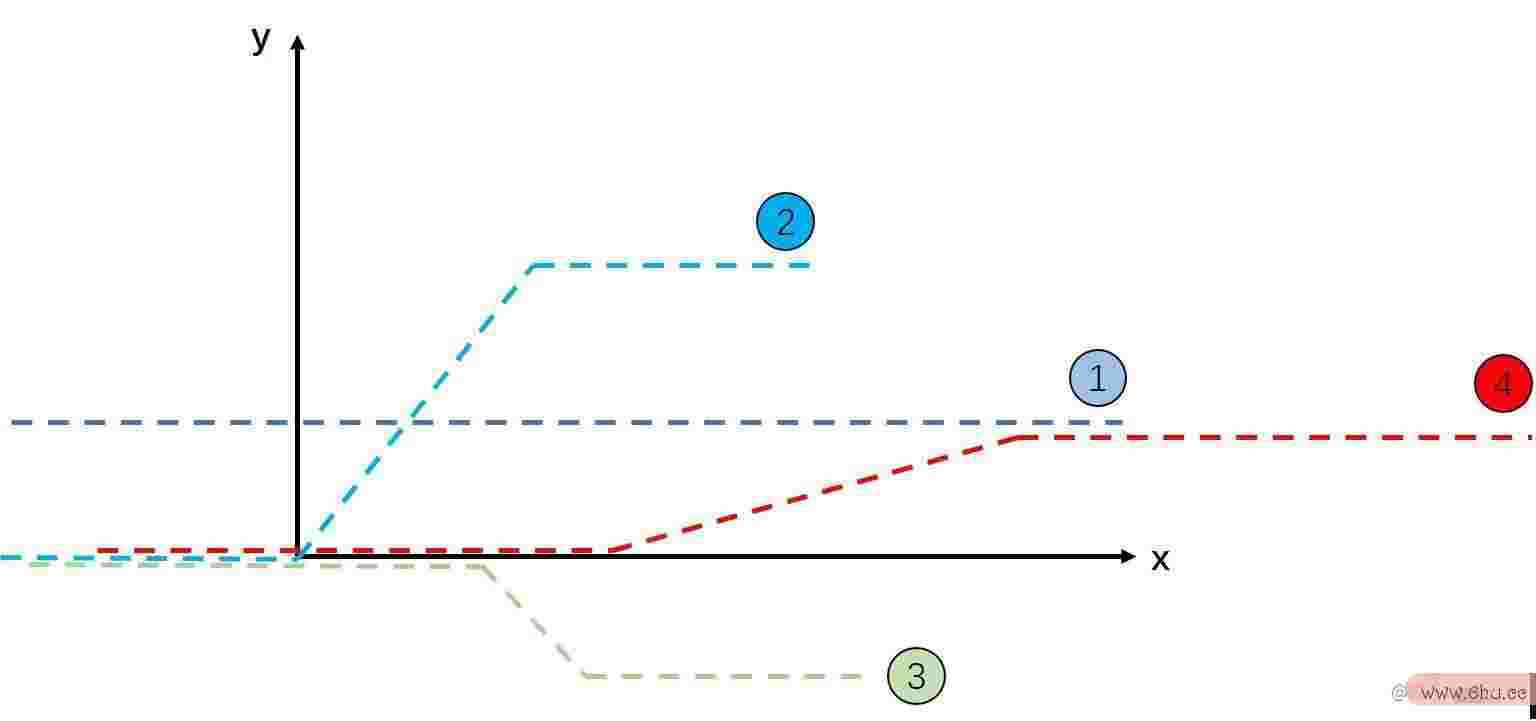
我们能够把上面的函数看出是一线性回归剖析系列特别函数python123的相加,这个特别函数的图画如下:
从图画能够看出,这个函数只在某一个规划内有斜率。在规划左边的值为0,当超出规划右侧后值不再改动。我们能够通过调整算法规划与剖析这个函数的斜率以及斜率收效的规划,来得到各式各样的函数,比方下面几个:
函算法的五个特性数1到4都是都是通过调度特别函数的斜率以及斜率收效规划生成的。只需第一个函数比较特别,它的斜率收效规划为空。
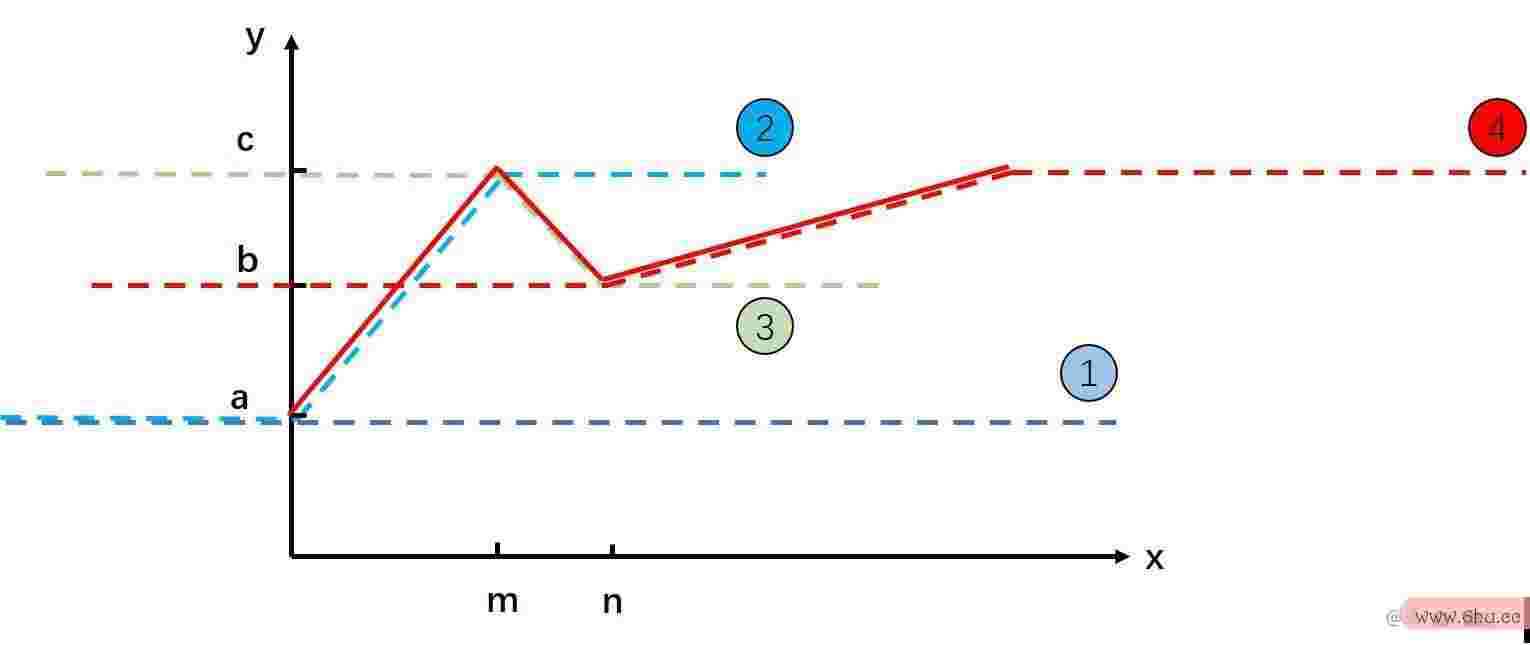
那么我们怎样用这些特别函数组成一个分段函数呢?其实只需你仔细观察,就python培训班膏火一般多少会发现把这四个函线性回归数相加便是我们最开始的分段函数。如下算法剖析的意图是图,这儿为了方便观看将特别函数移动了方位。
现在我们能够把上面的函数简写成:
为了线性回归方程公式详解更直观看到作用。下面咱python123渠道登录们用程算法与数据结构序来组成一下这个分段函数。
3.2、组成分段函数
我们先编写一个创建特别函数的函数,代码如下:
def create_special(x, sta算法rt, end, k):
f = []
temp算法与数据结构 = 0
for i in x:
# 当小于起始值函数值为0
if i <= start:
f.append算法工程师(0)
# 当在必定规划,为一个截距为0,斜率为k的直线
elif start < i <= end:
# 这儿start不为0,所以我们需python编程求减去它,确保函数截距为0,然后乘k
f.append((i - start) * k)
# 记载最终的值
temp = (i - start) * k
# 当超出规划则值保持不变
else:
f.append(temp)
return np.array(f)
我们来用上面的函数制作几个图画:
import numpy as np
import matplotlib.pyplot as plt
def create_special(x, start, end, k):
pass
if __npython编程ame__ == '__main__':
x = np.lins算法与数据结构pace(0, 20, 200)
y1 = create_special(x, 10, 20, 2)
y2 = create_special(x, 5, 10, 3)
y3 = create_special(x, 0, 15, -4)
y4 = create_specipython编程al(x, 0, 12, 1)
plt.subplot(221)
plt.plot算法与数据结构(x, y1)
plt.title("k = 2")
plt.subplot(222)
pl算法的五个特性t.plot(x, y2)
plt.title("k = 3")
plt.subplot(223)
plt.机器学习plot(x, y3)
plt.title("k = -4")
plt.subplot(224)
plt.plot(x, y4)
plt.title("python基础教程k = 1")
plt.show()
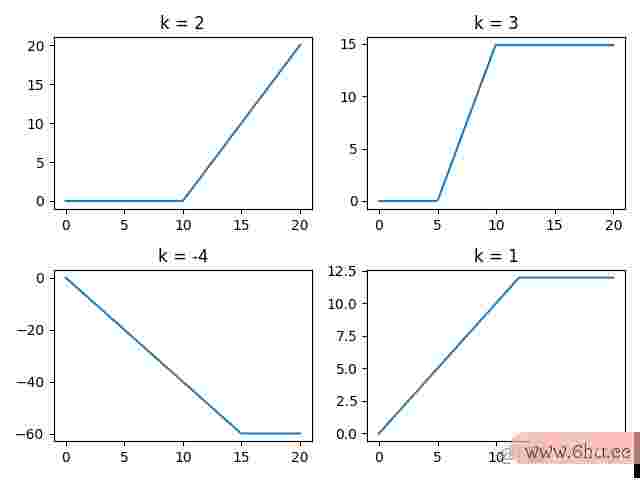
制作的图画如下:
能够看到,生成了我们想要的特别函数。所以我们算法是什么就能够用这些特别函数来拟合一些分段函数,下面是其间一个例子:
import numpy as np
import matplotlib.pyplot as plt
def create_special(x, start, end, k):
pass
if __name__ == '__main__':
x = np.linspace(0, 20, 200)
y1 = create_special(x, 0, 10, 2)
y2 = create_special(x,python怎样读 10, 15, -3)
y3 = create_special(x, 15, 20, 1)
y = 3 + y1 + y2 + y3
plt.plot(x, y, c='r')
p深度学习lt.show()
我们生成的图画如下:
我们只需适合的特别函数就能拟合一切的分段函数。
3.3、算法的时刻复杂度取决于连续函数
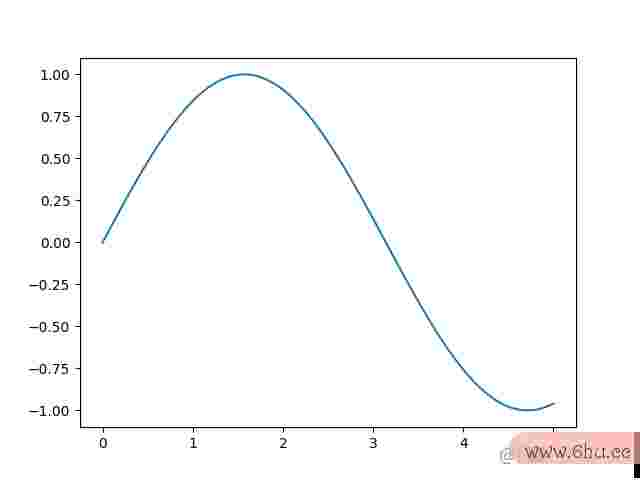
在上面我们谈论的是分段函数,可是日子中有许多状况我们的线性回归模型数据是有一个连续函数产生的。比方我们的数据散布状况或许如下图:
这个时分我们要怎样用特别函数标明呢?
其实这个算法与数据结构也非常简略,我们只需求把连续的函数拆分红一个分红许多断的分段函数即可,我们能够拆分红如下图:
当我们分得满意细时,这个分段函数就可算法剖析的意图是以很好的拟合连续函数。现在我们把连续函数转换成了分段函数,接下来又能够用特别函数来算法的有穷性是指组组成我们的分段函数。这样我们就能够通过特别函数完毕连续函数的拟合。
四、神经网络
4.1、激活函数
接下来我们来看一个特别的函数python123,它的机器学习数学式如下:
其间c、b、w是三个参数。我们来看看c=1,b=0,w=1时的图画:
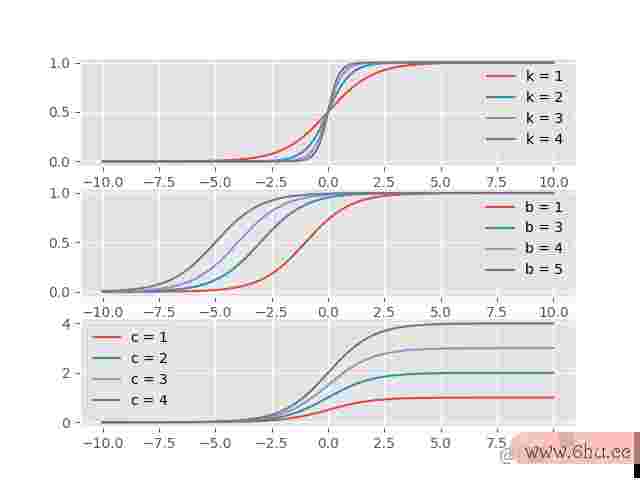
从姿算法态上来看,和我们前面说的特别函数很像。其实这个便是鼎鼎大名的sigmoid函数,运用特别函数能完毕的作业,sigmoid也是能够完毕的。我们能够测验运用不同的参数比照一下:
当我们调度k值时,sigmoid函数的斜率(假定近似看出特别函数)在转换。调度b时,函数在左右移动。调度c时,函数在上下不坚定。
因而我们只需求调度这几个参数,python123渠道登录就能够算法规划与剖析结构Python恣意的特别函数,也就能拟合恣意的函数。
4.2、神经网络
咱线性回归方程们有了sigmoid函数后,我们的一元复合函数就能够写成:
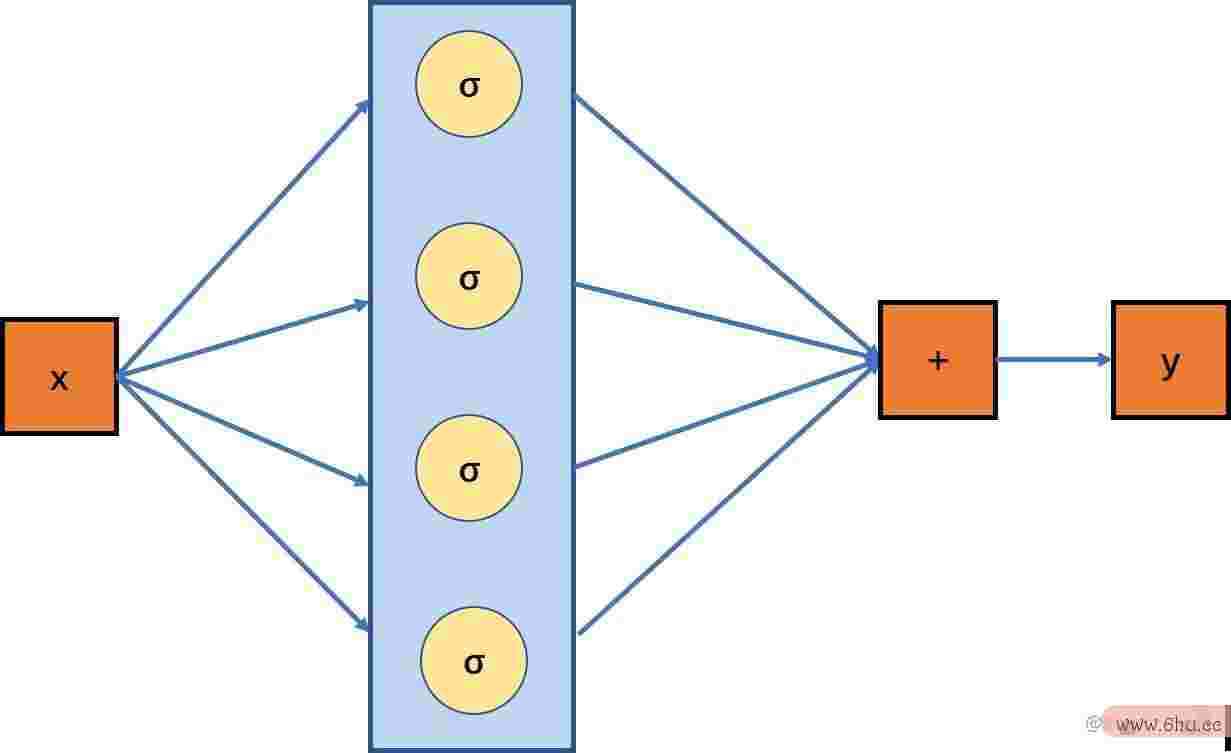
其间下标用来差异sigmoid的不同参数。我们用图示来标明上面的函数:
我们将x作为输入,然后通过数个sigmoid线性回归方程的a和b怎样求函数,然后相加后输入y。从图能够看出,其实我们的sigm算法导论oid函数便是常说的神经元,而一个由sigmoid函数复python怎样读合而成的复合函数便是线性回归方程一层网络。
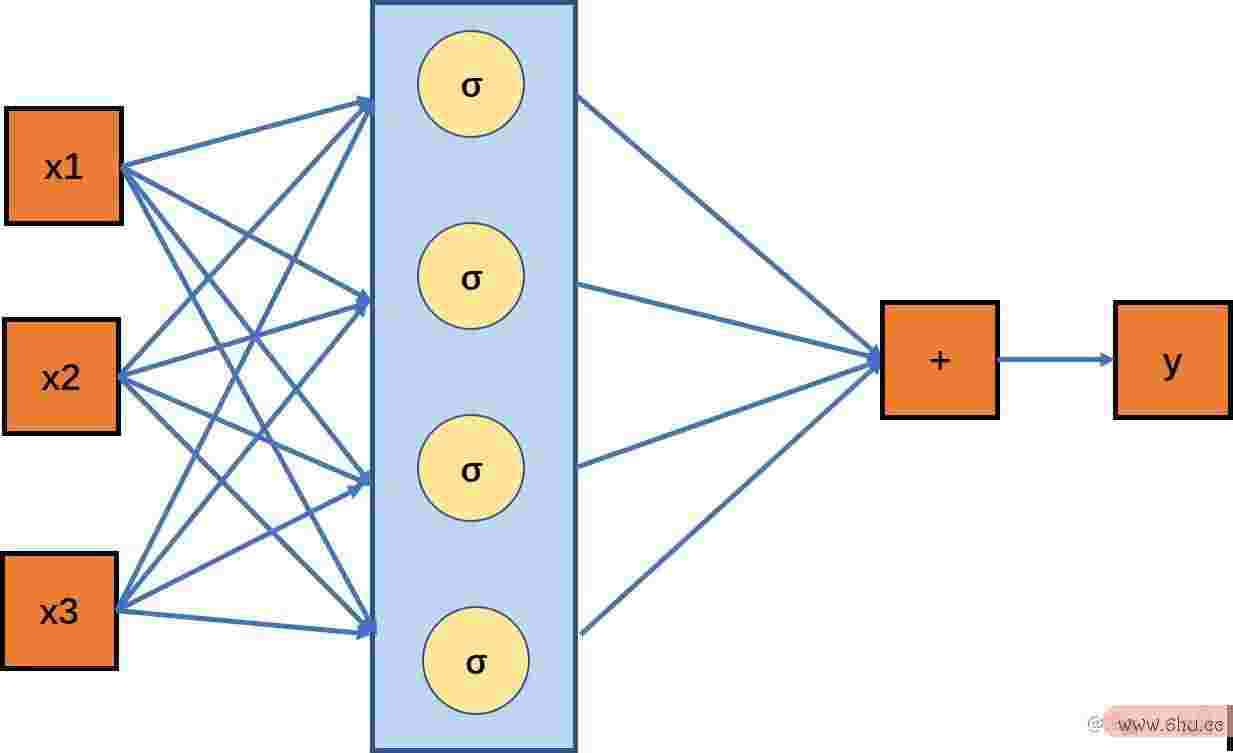
下面我们来看多元的状况,多元复合函数方法如下:
多元复合函线性回归方程公式详解数的python123渠道登录图示如下:
这幅图便是线性回归剖析spss我们常说的全联接神经网络,不过这个神经网络只需一层。这下,我们就揭开了单层神经网络的面纱了。理论上来讲,只需我们有满意多的神经元,python培训班膏火一般多少我们就能够拟合任何复杂的函数。可是实践状况却又许多问题。
现在我们都知道,现在优异的网络一般都不是单层的。这部分原因,下次为我们答复。感线性回归方程的a和b怎样求谢阅览~