这是我参与8月更文应战的第20天,活动概略检查:8月更文应战
为了同享此篇文章,个人做了许多的作业,所以未经自己附和,请勿转载,在此标明感谢!
层次聚类法(Hierachical clustering)
现在时变量的界说代节奏越来越快,咱们都喜爱吃快餐,看短视频,当然能够节约许多时刻去干自己愿意做的事。但是咱们也很难沉下心来往不断做好一件事。注意力也很难会集,或许遇事简略烦躁。其实许多事不是一瞬间就能马到成功,甚至有的时分是上下不坚决,即便尽力了回来让步,这时分就需要咱们坚持,累了烦了就休息一瞬间,文娱一下,只需坚持下来,相信会会有成效的。
有两种类型的分层聚类,分别是聚合式(Agglomerative)和割裂式(Div算法isive)数组词。
- 聚合式: 数据点的聚类是选用自下而上的方法,从单个数据点初步
- 割裂式(Divisive) : 全部的数据点都被视为一个大聚算法的时刻复杂度取决于类,聚类进程触及到将一个大聚类分红几个小聚类
在这篇文章中,咱们将要点评论触及自下而上方法的聚类。
聚类的一般进程
以下是聚类的进程。
- 初步时,将每个数据点视为一个聚类。初步时的聚类算法剖析的意图是数量为 K变量之间的联系思想导图 就是数算法是什么据点的数量
- 经过联接两个数组的界说最接近的数据点构成一个簇(类),然后构成 K-1 个簇(类)
- 经过联接两个最接近的聚类,构成更多的聚类,然后构成 K算法导论-2 聚类。
- 重复以上三个进程,直到全部样本点构成算法工程师一个大的聚类
- 构成了一个聚类,就能够运用树状图用于不同使命来划分红多个聚类
有不同的算法是什么方法来寻找群组之间的变量min表示什么类型的变量间隔。间隔自身可所以欧几里得间隔变量min表示什么类型的变量或曼哈顿间隔。以下是丈量两个集群之间间隔的一些备选方法
- 丈量两个聚类中最接近的点之间的间隔
- 丈量两个群组中最远的点之数组词间的间隔
- 丈量两个集群的中心点之间的间隔
- 丈量两个簇变量是什么意思之间全部或许的组合点之间的间隔,并取数组去重其平均值
树状图在分层聚类中的作用
一个大聚类由小聚类组合而成,组合联系可用树状图来标明,就被用来将聚类实践分变量类型有哪些割成多个相关数据点的聚类。让咱们来看看它究竟变量是怎样做数组公式的。
接下来咱们用 numpy 数组标明的数据点集结,如下所示。
X = np.a变量rray([[5,3],
[10,15],
[15,12],
[24,10],
[30,30],
[85,70],
[71,80],
[60,78],
[70,5数组词5]变量min表示什么类型的变量,
[80,91],算法设计与剖析])
impor变量之间的联系思想导图t matplotlib.pyplot as plt
labels = rang数组词e(1算法的有穷性是指, 11)
plt.figure(figsize=(10, 7))
plt.sub变量之间的联系plots_adjust(bottom=0.1)
plt.scatter(X[:,0],X[:,1], label='True P数组去重方法osition')
for label, x, y in zip(labels, X[:, 0], X[:, 1]):
plt.an数组去重notate(
label,
xy=(x, y), xytext=(-3, 3),
textc变量名的命名规矩oords='offset points', ha='right', va='bottom')
plt.show()
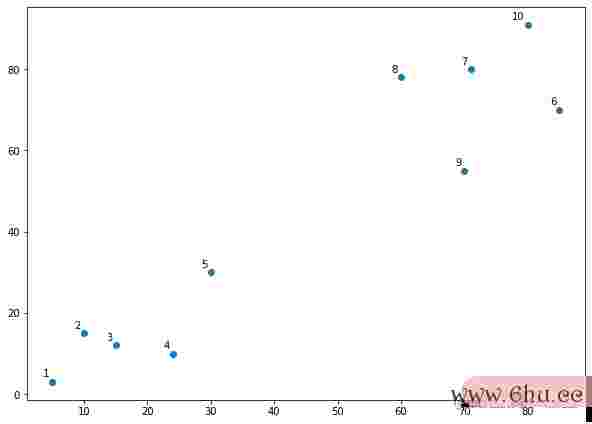
将样本点制作到图上数组词便于查询,而变量之间的联系思想导图且给每个点一个标明,标明该样本数组公式点详细是哪一个点。
在上图中,咱们不难发现样布点显着分为 2 群,图的做左下方(1-5)为一群而图右上方(6-10)又是一个群。但是实践问题中,样本点数量或许有是不计其数,并且数据点维度都是高维的数据。在这种情况下,咱们仅凭查询是无法发现规矩的。
回到层次聚类(hierarchical clustering)中树状图的运用,经过 scipy 库供给功用,咱们能够将样本点制作成树状图。
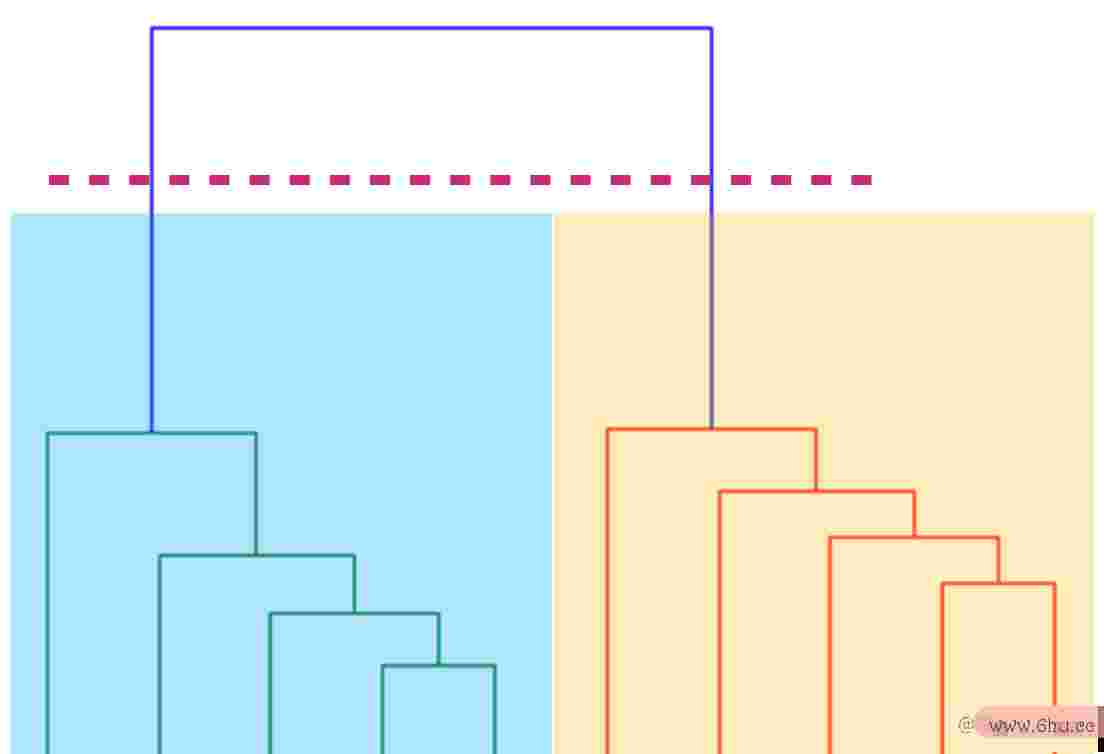
该算法首要在欧氏间隔的基础上找到彼此最接近的两个点。假定咱们回忆一下图1,就能够看到 2 和 3 样本点彼此最接近,而 7 和 8 样本点则彼此最接近。因此这两个点之间将首要构成一个集群。在图 2 中,现已样点 2 和 3 联接标明他们坐落一个群,算法的时刻复杂度取决于以及点 8 和 7 的树状图。从图2 能够看出,8 和 7 样本点之间的欧氏间隔大于 2算法 和 3 点之间的间隔。
下一步是将两点构成的聚类与下一个最近的聚类或点联接起来,这变量的界说又会构成另一个聚类。假定你看一下图表1,第 4 点离第 2 和第 3 点的聚类最近算法的时刻复杂度取决于,因变量min表示什么类型的变量此在图表 2 中,将第 4 点与第 2 和第 3 点的树状图联接起来,然后得到新的树状图。这个进程一向持续到全部的点被联接在一起构成一个大的聚类。
当构成一个大的聚类后,能够在树状图同水平划线来来进行聚类,不同算法方位水平线会得到不同类别的聚类方法。
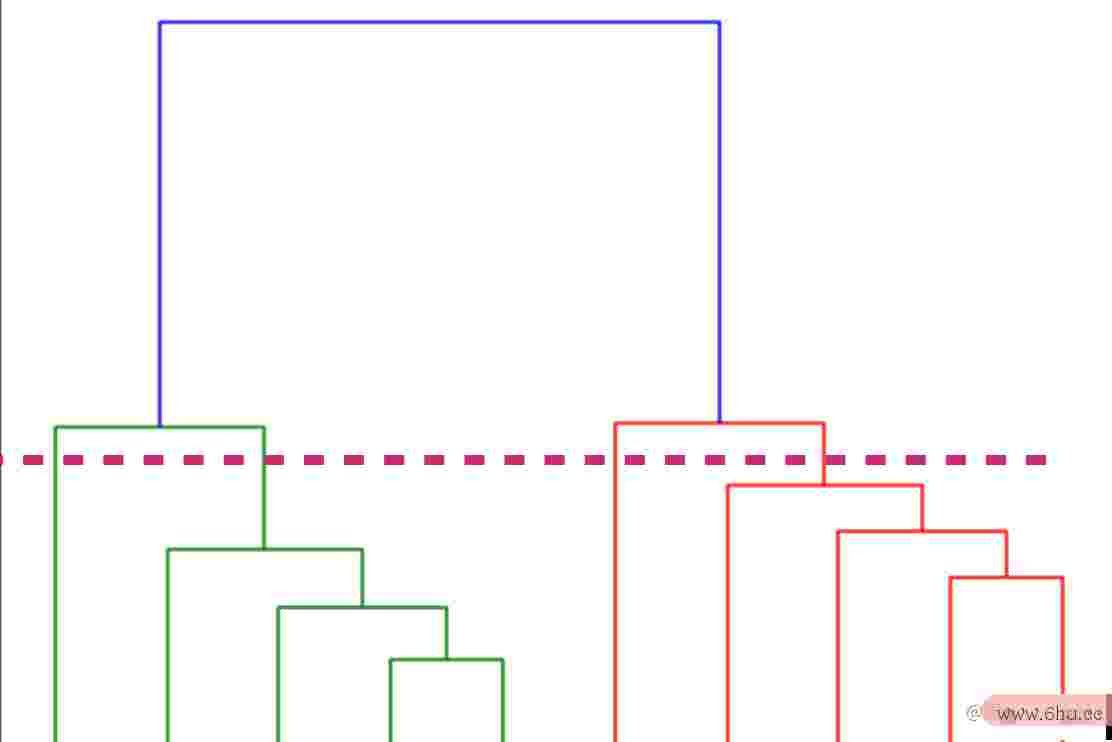
咱们能够看到,没有任何水平线经过的最大垂直间隔是由蓝线标明的。所以咱们画一条新的水平红线,穿过蓝线,由于数组转字符串在两点上与蓝线相交,因变量之间的联系此集群的数量将是 2。
基本上,这条水平线是一个阈值,它界说了成为一个独立集群所需的最小间隔。假定咱们再往下画一条线,成变量的界说为一个新聚类所需的阈值就会下降,更多的聚类就会构成,如下图所示。
在上图中,水平线穿过四条变量类型有哪些垂直线,导致四个集群:6、7、8 和 10 点的集群,3、2、4 点的集群,9 和 5 点将被视为单点的集群。
下一步是导入聚类的类,并调用其fit变量之间的联系思想导图_predict方法来猜想每个数据点所属的聚类算法与数据结构。
fro数组去重方法m sklearn.cluster import AgglomerativeClustering
cluster = AgglomerativeClusteri数组排序ng(n_clusters=2, affinity='euclidean', linkage='ward')
cluster.fit_predict(X)
在上面的代码中,咱们从 sklearn.cluster 库中导入 AgglomerativeClustering类。运用n_clusters参数将参数的数量设置为 2,而亲和力设置为 euclide变量是什么意思an(数据点之间的间隔)。最终链接参数被设置为变量名的命名规矩 ward,这使得集群之间的变异最小。
接下来咱们从AgglomerativeClustering 类的变量 cluster 中调算法的时刻复杂度取决于用 fit_predict 方法。数组排序这个方法回来每个数据点所属的聚类的称号算法剖析的意图是。,看看数据点是怎么被变量英文聚类的。
prin数组函数的使用方法t(cluster.labels_)
输出是一个由10个元素组成的一维数组,对应于分配给咱们10个数据点的聚类。
[1 1 1 1 1 0 0 0 0]