1. 图画缩放

1.1 简介

图画缩放是指经过增加或减少像从来改变图画尺度的进程，是图画处理中常见的操作。图画缩放会触及功率和图画质量之间的权衡。

图画扩大（也称为上采样或插值）的首要意图是扩大原图画，以便在更高分辨率的显示设备上显示。可是，扩大图画并不能带来更多信息，因而图画质量会不可避免地受到影响。

图画缩小（也称为下采样）的首要意图是减小图画尺度，以便更有效地存储或传输。缩小图画能够保留更多信息，但图画细节会丢失。

1.2 图画缩放办法分类

  • 空间域办法：直接在图画像素空间进行操作。常见的空间域缩放办法包含：
    • 最近邻插值：简略快速，但图画质量较差。
    • 双线性插值：图画质量比最近邻插值好，但核算量更大。
    • 立方插值：图画质量比双线性插值好，但核算量更大。

常见空间域缩放办法的比较：

办法 长处 缺陷
最近邻插值 简略快速 容易发生锯齿
双线性插值 平滑图画 可能导致细节模糊
立方插值 作用更好 核算量较大
  • 频域办法：将图画转换为频域，然后在频域进行操作。常见的频域缩放办法包含：
    • 傅里叶插值：将图画转换为傅里叶频谱，然后依据缩放份额调整频谱巨细，再将逆傅里叶改换回图画空间。傅里叶插值能够保持图画边际锐度。图画质量较高，但核算量较大。
    • Lanczos 插值：一种改善的傅里叶插值算法，经过使用低通滤波器来消除频谱中的混叠现象，平衡了速度和质量，是常用频域算法之一。

2. 插值算法

图画插值算法是指在已知像素值的基础上，估量不知道像素值的数学办法。OpenCV 供给了多种插值算法，用于图画缩放、旋转、仿射改换等操作。

在数学的数值剖析领域中，内插，或称插值（英语：Interpolation），是一种经过已知的、离散的数据点，在范围内推求新数据点的进程或办法。

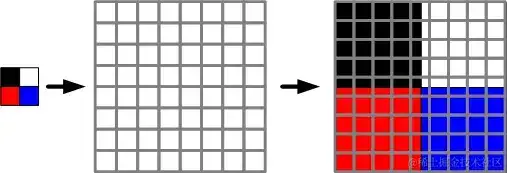
2.1 最近邻插值(Nearest Neighbor Interpolation)

最近邻插值经过找到方针像素在原图画中最近的像素值来赋值给方针像素。具体来说，依据原图画和方针图画的尺度，核算缩放的份额，然后依据缩放份额核算方针像素所依据的原像素，并将该值赋给方针像素。

srcx=dstxscalesrc_x = frac{dst_x}{scale}

srcy=dstyscalesrc_y = frac{dst_y}{scale}

其中， srcxsrc_x、srcysrc_y 表明原图画中的坐标， dstxdst_x、dstydst_y 表明方针图画中的坐标，scale 表明放缩倍数。

最近邻插值的长处:

  • 算法简略，核算量小，速度快。
  • 不会发生新的像素值，保持原始图画的灰度值。

最近邻插值的缺陷:

  • 容易发生锯齿现象，图画质量较低。

OpenCV 笔记(22)：图画的缩放——最近邻插值、双线性插值算法

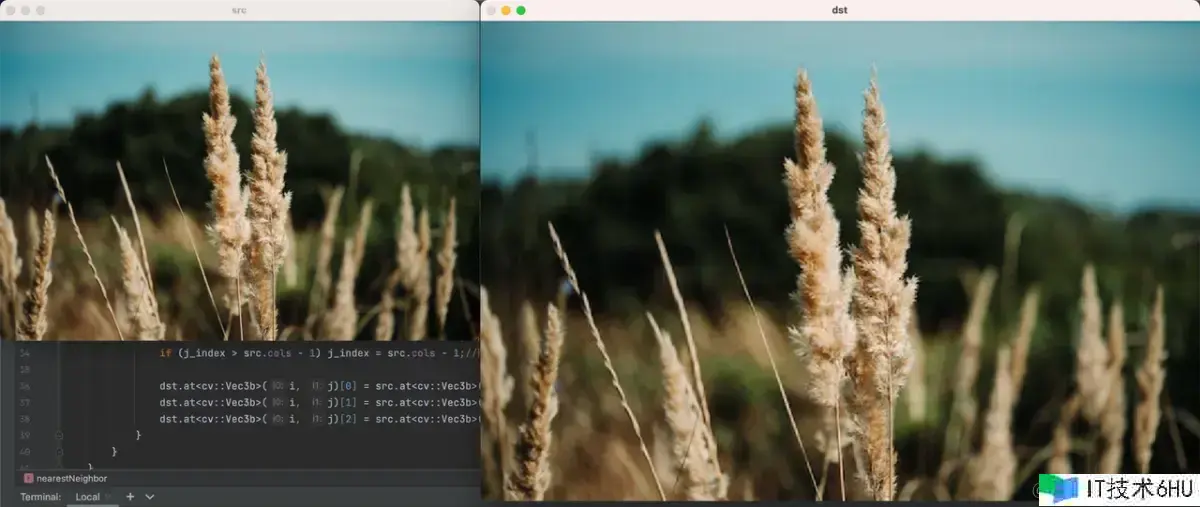
下面的代码，展示了怎么完成最近邻插值算法

#include "opencv2/highgui/highgui.hpp"
#include "opencv2/imgproc/imgproc.hpp"
using namespace std;
using namespace cv;
//最近邻插值算法
void nearestNeighbor(cv::Mat& src, cv::Mat& dst, float sx, float sy)
{
    // 由 scale 核算输出图画的尺度（四舍五入）
    int dst_cols = round(src.cols * sx);
    int dst_rows = round(src.rows * sy);
    dst = cv::Mat(dst_rows,dst_cols,src.type());
    for (int i = 0; i < dst.rows; i++){
        for (int j = 0; j < dst.cols; j++){
            if (src.channels() == 1) {
                // 插值核算，输出图画的像素点由原图画对应的最近的像素点得到（四舍五入）
                int i_index = round(i / sy);
                int j_index = round(j / sx);
                if (i_index > src.rows - 1) i_index = src.rows - 1;//避免越界
                if (j_index > src.cols - 1) j_index = src.cols - 1;//避免越界
                dst.at<uchar>(i, j) = src.at<uchar>(i_index, j_index);
            } else {
                // 插值核算，输出图画的像素点由原图画对应的最近的像素点得到（四舍五入）
                int i_index = round(i / sy);
                int j_index = round(j / sx);
                if (i_index > src.rows - 1) i_index = src.rows - 1;//避免越界
                if (j_index > src.cols - 1) j_index = src.cols - 1;//避免越界
                dst.at<cv::Vec3b>(i, j)[0] = src.at<cv::Vec3b>(i_index, j_index)[0];
                dst.at<cv::Vec3b>(i, j)[1] = src.at<cv::Vec3b>(i_index, j_index)[1];
                dst.at<cv::Vec3b>(i, j)[2] = src.at<cv::Vec3b>(i_index, j_index)[2];
            }
        }
    }
}
int main()
{
    Mat src = imread(".../grass.jpg");
    imshow("src", src);
    Mat dst;
    nearestNeighbor(src, dst,1.5, 1.5);
    imshow("dst", dst);
    waitKey(0);
    return 0;
}

OpenCV 笔记(22)：图画的缩放——最近邻插值、双线性插值算法

下面的代码，经过 Mat 的 forEach() 结合 C++11 lambda 表达式，完成对 Mat 对象快速像素遍历，从而重构了最近邻插值算法。

typedef cv::Point3_<uint8_t> Pixel;
//最近邻插值算法
void nearestNeighbor(cv::Mat& src, cv::Mat& dst, float sx, float sy)
{
    // 由 scale 核算输出图画的尺度（四舍五入）
    int dst_cols = round(src.cols * sx);
    int dst_rows = round(src.rows * sy);
    dst = cv::Mat(dst_rows,dst_cols,src.type());
    dst.forEach<Pixel>([&](Pixel &p, const int * position) -> void {
        int row = position[0];
        int col = position[1];
        if (src.channels() == 1) {
            int i_index = round(row / sy);
            int j_index = round(col / sx);
            dst.at<uchar>(row, col) = src.at<uchar>(i_index, j_index);
        } else {
            int i_index = round(row/ sy);
            int j_index = round(col / sx);
            dst.at<cv::Vec3b>(row, col)[0] = src.at<cv::Vec3b>(i_index, j_index)[0];
            dst.at<cv::Vec3b>(row, col)[1] = src.at<cv::Vec3b>(i_index, j_index)[1];
            dst.at<cv::Vec3b>(row, col)[2] = src.at<cv::Vec3b>(i_index, j_index)[2];
        }
    });
}

2.2 双线性插值(Bilinear Interpolation)

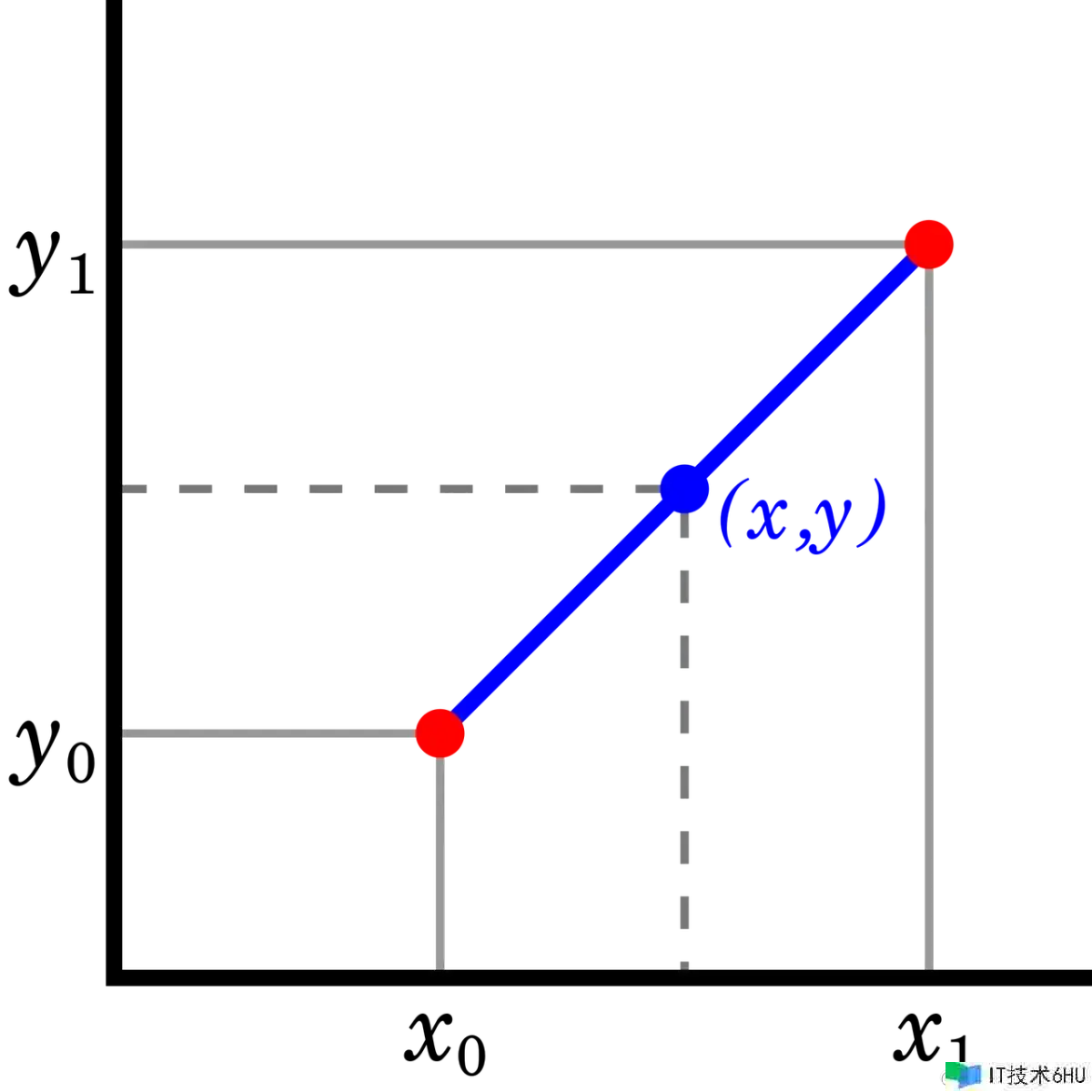
先介绍一下线性插值，线性插值是一种估量两个已知数据点之间的值的办法。

OpenCV 笔记(22)：图画的缩放——最近邻插值、双线性插值算法

假定咱们已知坐标 (x0x_0，y0y_0) 与 (x1x_1，y1y_1)，要得到 [x0x_0，x1x_1] 区间内某一方位 x 在直线上的值。由上图可得：

y−y0x−x0=y1−y0x1−x0frac{y-y_0}{x-x_0} = frac{y_1-y_0}{x_1-x_0}

因为 x 已知，则 y：

y=x1−xx1−x0y0+x−x0x1−x0y1y = frac{x_1-x}{x_1-x_0}y_0 + frac{x-x_0}{x_1-x_0}y_1

所以，这是在 x 方向进步行了一次线性插值。

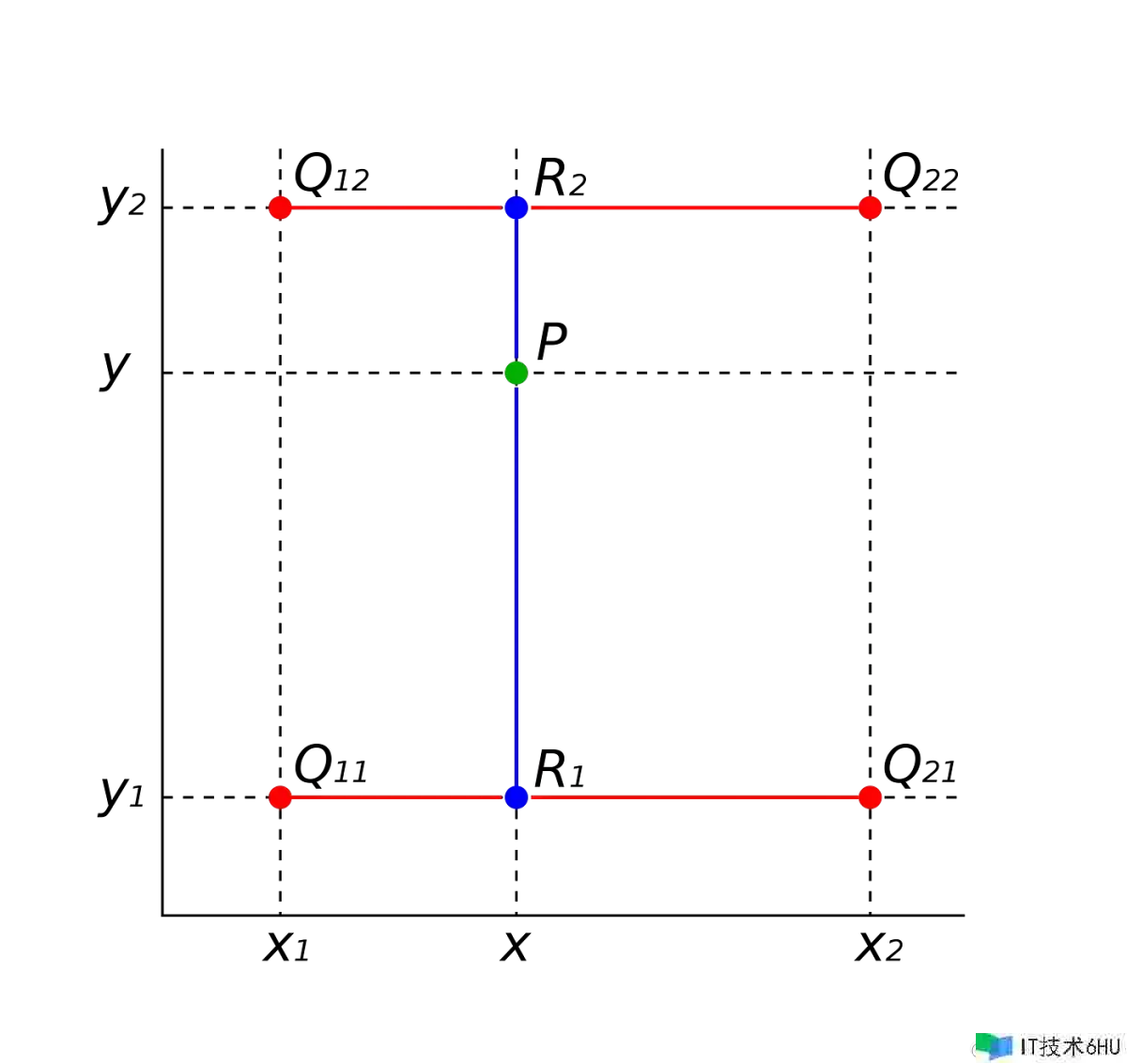
双线性插值是对 x 方向和 y 方向分别进行插值，它依据原始图画中四个相邻像素的值来估量新方位处像素的值。它是一维线性插值的扩展。

OpenCV 笔记(22)：图画的缩放——最近邻插值、双线性插值算法

在上图中，假定已知Q11Q_{11}、Q12Q_{12}、Q21Q_{21}、Q22Q_{22}四个点，咱们要估量由这四个点组成的矩形内的恣意点(x,y)处像素值 f(x,y) 。

  • 对沿 y 轴的两对点 Q11Q_{11}、Q21Q_{21}在 x 方向进行线性插值：

f(R1)=x2−xx2−x1f(Q11)+x−x1x2−x1f(Q21)f(R_1)= frac{x_2-x}{x_2-x_1}f(Q_{11}) + frac{x-x_1}{x_2-x_1}f(Q_{21})

  • 对沿 y 轴的两对点 Q12Q_{12}、Q22Q_{22}在 x 方向进行线性插值：

f(R2)=x2−xx2−x1f(Q12)+x−x1x2−x1f(Q22)f(R_2)= frac{x_2-x}{x_2-x_1}f(Q_{12}) + frac{x-x_1}{x_2-x_1}f(Q_{22})

  • 对沿 x 轴的两对点 R1R_1、R2R_2在 y 方向进行线性插值：

f(P)=y2−yy2−y1f(R1)+y−y1y2−y1f(R2)f(P)= frac{y_2-y}{y_2-y_1}f(R_1) + frac{y-y_1}{y_2-y_1}f(R_2)

此时，一共执行了三次线性插值，双线性插值仅仅对 x、y 方向进行插值，而不是进行两次插值。

双线性插值用于依据原始图画中的已知值来估量调整巨细的图画中像素的强度或色彩值。 与最近邻插值比较，这种办法能够发生更平滑的结果，后者可能会导致可见的伪影或锯齿状边际。

下面的代码，展示了怎么完成双线性插值算法。

#include <opencv2/opencv.hpp>
using namespace cv;
using namespace std;
typedef cv::Point3_<uint8_t> Pixel;
// 双线性插值算法
void bilinearInterpolation(Mat& src, Mat& dst, double sx, double sy) {
    int dst_rows = static_cast<int>(src.rows * sy);
    int dst_cols = static_cast<int>(src.cols * sx);
    dst = Mat::zeros(cv::Size(dst_cols, dst_rows), src.type());
    dst.forEach<Pixel>([&](Pixel &p, const int * position) -> void {
        int row = position[0];
        int col = position[1];
        // (col,row)为方针图画坐标
        // (before_x,before_y)原图坐标
        double before_x = double(col + 0.5) / sx - 0.5f;
        double before_y = double(row + 0.5) / sy - 0.5;
        // 原图画坐标四个相邻点
        // 获得改换前最近的四个极点,取整
        int top_y = static_cast<int>(before_y);
        int bottom_y = top_y + 1;
        int left_x = static_cast<int>(before_x);
        int right_x = left_x + 1;
        //核算改换前坐标的小数部分
        double u = before_x - left_x;
        double v = before_y - top_y;
        // 如果核算的原始图画的像素大于真实原始图画尺度
        if ((top_y >= src.rows - 1) && (left_x >= src.cols - 1)) {//右下角
            for (size_t k = 0; k < src.channels(); k++) {
                dst.at<Vec3b>(row, col)[k] = (1. - u) * (1. - v) * src.at<Vec3b>(top_y, left_x)[k];
            }
        } else if (top_y >= src.rows - 1) { //最后一行
            for (size_t k = 0; k < src.channels(); k++) {
                dst.at<Vec3b>(row, col)[k]
                        = (1. - u) * (1. - v) * src.at<Vec3b>(top_y, left_x)[k]
                          + (1. - v) * u * src.at<Vec3b>(top_y, right_x)[k];
            }
        } else if (left_x >= src.cols - 1) {//最后一列
            for (size_t k = 0; k < src.channels(); k++) {
                dst.at<Vec3b>(row, col)[k]
                        = (1. - u) * (1. - v) * src.at<Vec3b>(top_y, left_x)[k]
                          + (v) * (1. - u) * src.at<Vec3b>(bottom_y, left_x)[k];
            }
        } else {
            for (size_t k = 0; k < src.channels(); k++) {
                dst.at<Vec3b>(row, col)[k]
                        = (1. - u) * (1. - v) * src.at<Vec3b>(top_y, left_x)[k]
                          + (1. - v) * (u) * src.at<Vec3b>(top_y, right_x)[k]
                          + (v) * (1. - u) * src.at<Vec3b>(bottom_y, left_x)[k]
                          + (u) * (v) * src.at<Vec3b>(bottom_y, right_x)[k];
            }
        }
    });
}
int main() {
    Mat src = imread(".../grass.jpg");
    imshow("src", src);
    double sx = 1.5;
    double sy = 1.5;
    Mat dst;
    bilinearInterpolation(src,dst, sx, sy);
    imshow("dst", dst);
    waitKey(0);
    return 0;
}

OpenCV 笔记(22)：图画的缩放——最近邻插值、双线性插值算法

3. 总结

图画缩放是图画处理中一项重要的技术，具有广泛的使用场景。

本文介绍了两种比较简略的插值算法：最近邻插值、双线性插值。最近邻插值适合于需求保持图画原始灰度值或边际清晰度的场景。双线性插值适合于需求平滑图画的场景。如果需求更高的图画质量，能够考虑使用其他插值算法，例如立方插值或 Lanczos 插值，后续的文章也会介绍它们。