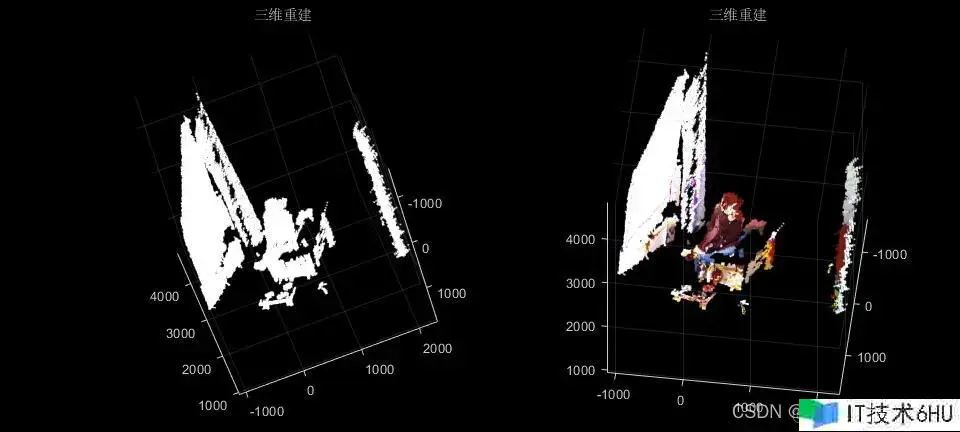
1.算法运转效果图预览
2.算法运转软件版别
matlab2022a
3.算法理论概述
三维室内场景建模在计算机视觉、机器人导航、虚拟现实等领域有广泛使用。传统的建模办法一般根据激光扫描仪或深度相机,但这些设备价格昂贵且不易普及。根据双目RGB图画和图画深度信息的建模方规律具有成本低、易于推广的优点。
3.1 双目视觉原理
双目视觉是模仿人类双眼观察物体的方式,经过两个不同视角的图画获取物体的三维信息。其中心原理是视差(Disparity)计算。
假定左右两个相机的焦距为f,基线距(两相机中心间隔)为B,物体在左图画和右图画中的像素坐标分别为(xl,yl)(x_l, y_l)(xl,yl)和(xr,yr)(x_r, y_r)(xr,yr),则物体的深度Z可计算为:
Z=fBxl−xrZ = frac{fB}{x_l – x_r}Z=xl−xrfB
此公式是根据理想情况下的双目视觉模型,实践使用中还需求考虑相机校对、图画匹配等问题。
3.2 深度信息获取
除了双目视觉,还能够经过其他办法获取图画的深度信息,如结构光法、飞翔时刻法等。这些办法各有优缺点,适用于不同场景。
经过双目视觉或其他办法获取深度信息后,能够将二维图画中的每个像素点映射到三维空间中,形成三维点云。点云的生成触及相机内参和外参的标定。
假定相机内参矩阵为K,外参矩阵为[R∣T][R|T][R∣T],对于图画中的一点p=(u,v,1)Tp = (u, v, 1)^Tp=(u,v,1)T,其对应的三维空间点P=(X,Y,Z)TP = (X, Y, Z)^TP=(X,Y,Z)T满足:
p=K[R∣T]Pp = K[R|T]Pp=K[R∣T]P
经过解这个方程,能够得到点P的三维坐标。遍历图画中的一切像素,即可生成三维点云。
3.3 外表重建
生成三维点云后,需求进行外表重建以得到完好的三维模型。常用的外表重建办法有Delaunay三角剖分、Poisson外表重建等。这些办法旨在根据点云的空间分布,构建出光滑的外表模型。
4.部分中心程序 `%读取左右RGB图画和对应的深度图画以进行校准
% 左RGB图画和对应的深度图画
Image_L = imread(‘imagesImage_L.png’);% 读取左RGB图画
Dep_L = imread(‘imagesDep_L.png’);% 读取左深度图画
% 右RGB图画和对应的深度图画
Image_R = imread(‘imagesImage_R.png’);% 读取右RGB图画
Dep_R = imread(‘imagesDep_R.png’);% 读取右深度图画
figure();
subplot(221);
imshow(Image_L );
title(‘双目左图’)
subplot(222);
imshow(Dep_L,[0.8,3.0]);
title(‘双目左图深度信息’)
subplot(223);
imshow(Image_R);
title(‘双目右图’)
subplot(224);
imshow(Dep_R,[0.8,3.0]);
title(‘双目右图深度信息’)
%将深度图画中的一切2D点反投影到3D空间中(针对左相机)
%左相机的2D点:
Dep_Lmap = func_2D_2_3D(Dep_L,Cdx,Cdy,Fdx,Fdy);
%将深度图画中的一切2D点反投影到3D空间中(针对右相机)
%右相机的2D点:
Dep_Rmap = func_2D_2_3D(Dep_R,Cdx,Cdy,Fdx,Fdy);
%将一切变换后的3D点投影到RGB图画上(针对左相机)
% 左相机投影:
[Image_Lp1,Image_Lp2] = func_3D_POINT(Image_L,Dep_L,Dep_Lmap,mat_rot,mat_tra,FLx_cam,FLy_cam,CLx_cam,CLy_cam);
% 右相机投影:
[Image_Rp1,Image_Rp2] = func_3D_POINT(Image_R,Dep_R,Dep_Rmap,mat_rot,mat_tra,FRx_cam,FRy_cam,CRx_cam,CRy_cam);
%将左相机的3D坐标转换为右相机的3D坐标体系
len = length(Image_Lp1);
pc_RGB_left_right = zeros(len, 3);
for i=1:len
pc_RGB_left_right(i, :) = (I_R * Image_Lp1(i, :)’ I_tras’)’;
end
%将左右两个相机的点云合并并显现终究重建的图画
figure
subplot(121);
pcshow([pc_RGB_left_right; Image_Rp1], [Image_Lp2; Image_Rp2]);
title(‘三维重建’)
view([150,-120]);
subplot(122);
pcshow([pc_RGB_left_right; Image_Rp1], [Image_Lp2; Image_Rp2]/128);
title(‘三维重建’)
view([150,-120]);`