养成好习惯,先赞后看哦~
所属专栏:数据结构与算法 贝蒂的主页:Betty‘s blog
前语
跟着使用程序变得越来越复杂和数据越来越丰富,几百万、几十亿乃至几百亿的数据就会呈现,而对这么大对数据进行查找、刺进或许排序等的操作就越来越慢,人们为了处理这些问题,进步对数据的办理功率,提出了一门学科即:数据结构与算法
1. 什么是数据结构
**数据结构(Data Structure)**是核算机存储、安排数据的办法,指相互之间存在一种或多种特定联系的数据元素的集合。
下标是常见的数据结构:
| 名称 | 界说 |
|---|---|
| 数组(Array) | 数组是一种聚合数据类型,它是将具有相同类型的若干变量有序地安排在一起的集合。 |
| 链表(Linked List) | 链表是一种数据元素依照链式存储结构进行存储的数据结构,这种存储结构具有在物理上存在非连续的特点。 |
| 栈(Stack) | 栈是一种特别的线性表,它只能在一个表的一个固定端进行数据结点的刺进和删去操作 |
| 队列(Queue) | 队列和栈类似,也是一种特别的线性表。和栈不同的是,队列只允许在表的一端进行刺进操作,而在另一端进行删去操作。 |
| 树(Tree) | 树是典型的非线性结构,它是包括,2 个结点的有穷集合 K |
| 堆(Heap) | 堆是一种特别的树形数据结构,一般评论的堆都是二叉堆。 |
| 图(Graph) | 图是另一种非线性数据结构。在图结构中,数据结点一般称为极点,而边是极点的有序偶对 |
2. 什么是算法
**算法(Algorithm):**便是界说杰出的核算进程,他取一个或一组的值为输入,并产生出一个或一组值作为输出。简略来说算法便是一系列的核算步骤,用来将输入数据转化成输出成果。
算法一般分为:排序,递归与分治,回溯,DP,贪心,查找算法
- 算法往往数学密切相关,就如数学题一样,每道数学题都有不同的解法,算法也是同理。
3. 复杂度剖析
3.1 算法评价
咱们在进行算法剖析时,常常需求完结两个方针**。一个是找出问题的处理办法,另一个便是找到问题的最优解**。而为了找出最优解,咱们就需求从两个维度剖析:
- 时刻功率:算法运转的快慢
- 空间功率:算法所占空间的巨细
3.2 评价办法
评价时刻的办法首要分为两种,一种是试验剖析法,一种是理论剖析法。
(1) 试验剖析法
试验剖析法简略来说便是将不同种算法输入同一台电脑,统计时刻的快慢。可是这种办法有两大缺陷:
- 无法排查试验本身条件与环境的条件的影响:比如同一种算法在不同装备的电脑上的运算速度或许彻底不同,乃至成果彻底相反。咱们很难排查一切情况。
- 本钱太高:同一种算法或许在数据少时体现不显着,在数据多时速率较快
(2) 理论剖析法
由于试验剖析法的局限性,就有人提出了一种理论测评的办法,便是渐近复杂度剖析(asymptotic complexity analysis),简称复杂度剖析。
这种办法体现算法运转所需的时刻(空间)资源与输入数据巨细之间的联系,能有用的反响算法的优劣。
4. 时刻复杂度与空间复杂度
4.1 时刻复杂度
一个算法所花费的时刻与其间句子的执行次数成正比例,算法中的根本操作的执行次数,为算法的时刻复杂度。
为了准确的表述一段代表所需时刻,咱们先假定赋值(=)与加号( )所需时刻为1ns,乘号()所需时刻为2ns,打印所需为3ns。
让咱们核算如下代码所需总时刻:
int main()
{
int i = 1;//1ns
int n = 0;//1ns
scanf("%d", &n);
for (i = 0; i < n; i )
{
printf("%d ", i);//3ns
}
return 0;
}
核算时刻如下:
可是实际上统计每一项所需时刻是不现实的,并且由于是理论剖析,当n—>∞时,其余项皆可疏忽,T(n)的数量级由最高阶决定。所以咱们核算时刻复杂度时,能够简化为两个步骤:
- 疏忽除最高阶以外的一切项。
- 疏忽一切系数。
而上述代码时刻能够记为O(n),这种办法被称为大O的渐进表明法。假如核算机成果满是常数,则记为O(1)。
- 并且核算复杂度时,有时候会呈现不同情况的成果,这是应该以最坏的成果考虑。
4.2 空间复杂度
空间复杂度也是一个数学表达式,是对一个算法在运转进程中临时占用存储空间巨细的测量 。空间复杂度的表明也遵循大O的渐进表明法
让咱们核算一下冒泡排序的空间复杂度
// 核算BubbleSort的空间复杂度?
void BubbleSort(int* a, int n)
{
assert(a);
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i < end; i)
{
if (a[i - 1] > a[i])
{
Swap(&a[i - 1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}
- 经过观察咱们能够看出,冒泡排序并没有拓荒多余的空间,所以空间复杂度为O(1).
5. 复杂度分类
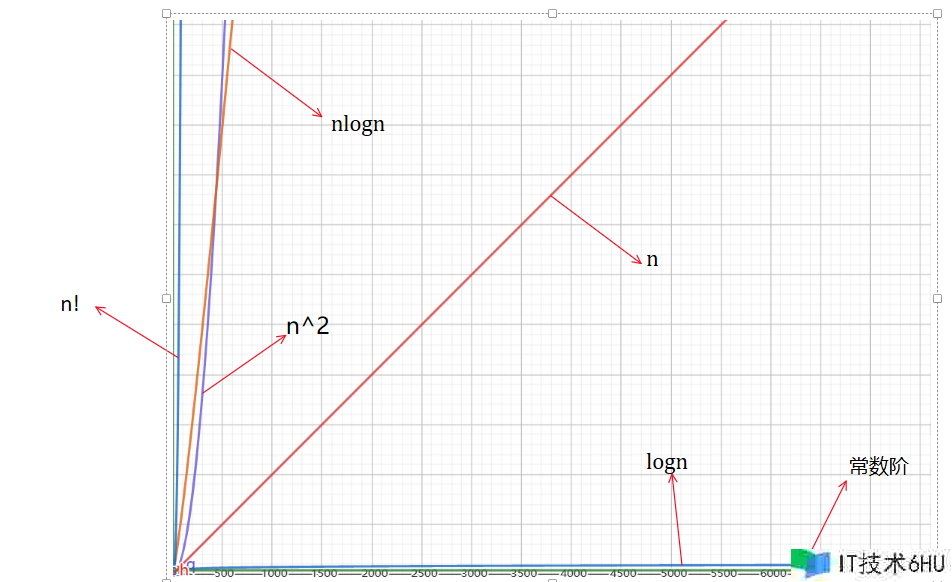
算法的复杂度有几个量级,表明如下:
- 从左到右复杂度依次递加,算法的缺点也就越显着
图示如下:
5.1 常数O(1)阶
常数阶是一种十分快速的算法,可是在实际使用中十分难完成
以下是一种时刻复杂度与空间复杂度皆为O(1)的算法:
int main()
{
int a = 0;
int b = 1;
int c = a b;
printf("两数之和为%dn", c);
return 9;
}
5.2 对数阶O(logN)
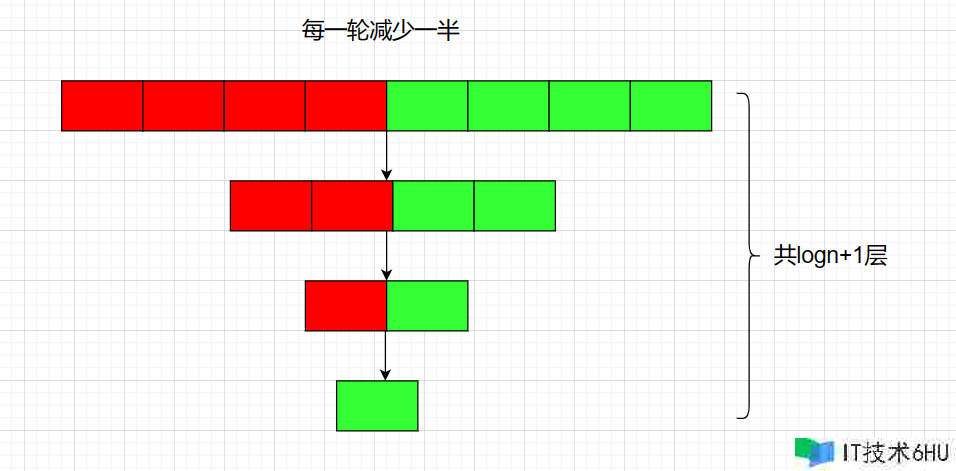
对数阶是一种比较快的算法,它一般每次削减一半的数据。咱们常用的二分查找算法的时刻复杂度就为O(logN)
二分查找如下:
int binary_search(int nums[], int size, int target) //nums是数组,size是数组的巨细,target是需求查找的值
{
int left = 0;
int right = size - 1; // 界说了target在左闭右闭的区间内,[left, right]
while (left <= right) { //当left == right时,区间[left, right]依然有用
int middle = left ((right - left) / 2);//等同于 (left right) / 2,防止溢出
if (nums[middle] > target) {
right = middle - 1; //target在左区间,所以[left, middle - 1]
} else if (nums[middle] < target) {
left = middle 1; //target在右区间,所以[middle 1, right]
} else { //既不在左面,也不在右边,那便是找到答案了
return middle;
}
}
//没有找到方针值
return -1;
}
空间复杂度为O(logN)的算法,一般为分治算法
比如用递归完成二分算法:
int binary_search(int ar[], int low, int high, int key)
{
if(low > high)//查找不到
return -1;
int mid = (low high)/2;
if(key == ar[mid])//查找到
return mid;
else if(key < ar[mid])
return Search(ar,low,mid-1,key);
else
return Search(ar,mid 1,high,key);
}
每一次执行递归都会对应拓荒一个空间,也被称为栈帧。
5.3 线性阶O(N)
线性阶算法,时刻复杂度与空间复杂度跟着数量均匀改变。
遍历数组或许链表是常见的线性阶算法,以下为时刻复杂度为O(N)的算法:
int main()
{
int n = 0;
int count = 0;
scanf("%d", &n);
for (int i = 0; i < n; i )
{
count = i;//核算0~9的和
}
return 0;
}
以下为空间复杂度为O(N)的算法
int main()
{
int n = 0;
int count = 0;
scanf("%d", &n);
int* p = (int*)malloc(sizeof(int) * n);
//拓荒巨细为n的空间
if (p == NULL)
{
perror("malloc fail");
return -1;
}
free(p);
p=NULL;
return 0;
}
5.4 线性对数阶O(NlogN)
无论是时刻复杂度仍是空间复杂度,线性对数阶一般呈现在嵌套循环中,即一层的复杂度为O(N),另一层为O(logN)
比如说循环使用二分查找打印:
int binary_search(int nums[], int size, int target) //nums是数组,size是数组的巨细,target是需求查找的值
{
int left = 0;
int right = size - 1; // 界说了target在左闭右闭的区间内,[left, right]
while (left <= right) { //当left == right时,区间[left, right]依然有用
int middle = left ((right - left) / 2);//等同于 (left right) / 2,防止溢出
if (nums[middle] > target) {
right = middle - 1; //target在左区间,所以[left, middle - 1]
}
else if (nums[middle] < target) {
left = middle 1; //target在右区间,所以[middle 1, right]
}
else { //既不在左面,也不在右边,那便是找到答案了
printf("%d ", nums[middle]);
}
}
//没有找到方针值
return -1;
}
void func(int nums[], int size, int target)
{
for (int i = 0; i < size; i )
{
binary_search(nums, size, target);
}
}
空间复杂度为O(NlogN)的算法,最常见的难道归并排序
void Merge(int sourceArr[],int tempArr[], int startIndex, int midIndex, int endIndex){
int i = startIndex, j=midIndex 1, k = startIndex;
while(i!=midIndex 1 && j!=endIndex 1) {
if(sourceArr[i] > sourceArr[j])
tempArr[k ] = sourceArr[j ];
else
tempArr[k ] = sourceArr[i ];
}
while(i != midIndex 1)
tempArr[k ] = sourceArr[i ];
while(j != endIndex 1)
tempArr[k ] = sourceArr[j ];
for(i=startIndex; i<=endIndex; i )
sourceArr[i] = tempArr[i];
}
//内部使用递归
void MergeSort(int sourceArr[], int tempArr[], int startIndex, int endIndex) {
int midIndex;
if(startIndex < endIndex) {
midIndex = startIndex (endIndex-startIndex) / 2;//防止溢出int
MergeSort(sourceArr, tempArr, startIndex, midIndex);
MergeSort(sourceArr, tempArr, midIndex 1, endIndex);
Merge(sourceArr, tempArr, startIndex, midIndex, endIndex);
}
}
5.5 平方阶O(N^2^)
平方阶与线性对数阶类似,常见于嵌套循环中,每层循环的复杂度为O(N)
时刻复杂度为O(N^2^),最常见的便是冒泡排序
void BubbleSort(int* a, int n)
{
assert(a);
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i < end; i)
{
if (a[i - 1] > a[i])
{
Swap(&a[i - 1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}
核算进程如下;
空间复杂度为O(N^2^),最简略的便是动态拓荒。
{
int n = 0;
int count = 0;
scanf("%d", &n);
int* p = (int*)malloc(sizeof(int) * n*n);
//拓荒巨细为n的空间
if (p == NULL)
{
perror("malloc fail");
return -1;
}
free(p);
p=NULL;
return 0;
}
5.6 指数阶O(2^N^)
指数阶的算法功率低,并不常用。
常见的时刻复杂度为O(2^N^)的算法便是递归完成斐波拉契数列:
int Fib1(int n)
{
if (n == 1 || n == 2)
{
return 1;
}
else
{
return Fib1(n - 1) Fib1(n - 2);
}
}
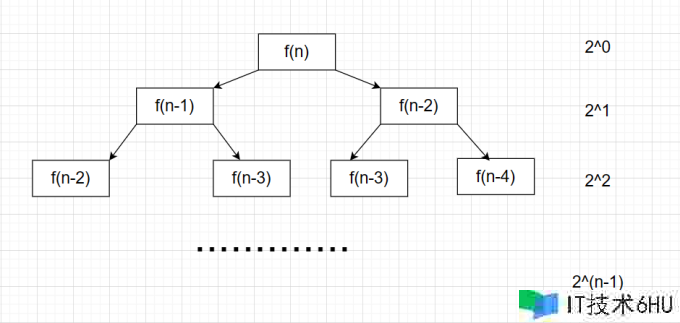
粗略估计
- 值得一提的是斐波拉契的空间复杂度为O(N),由于在递归至最深处后往回归的进程中,后续空间都在销毁的空间上树立的,这样能大大进步空间的利用率。
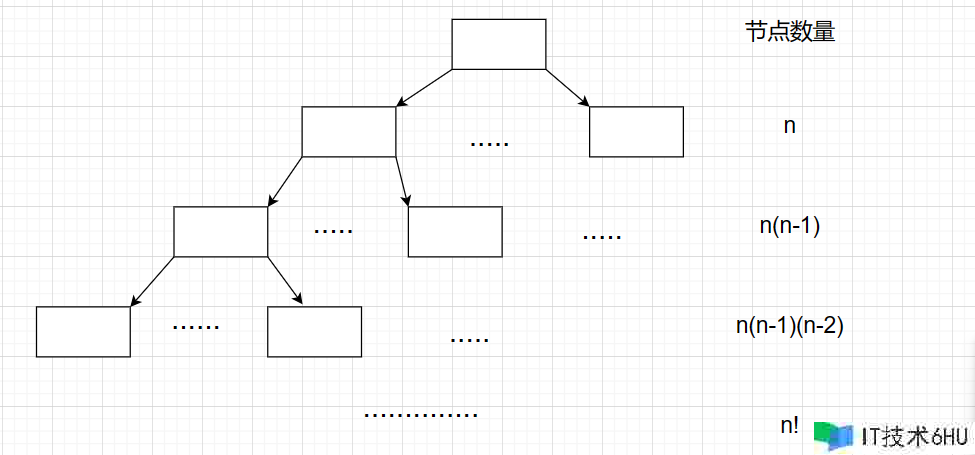
空间复杂度为O(2^N^)的算法一般与树有关,比如树立满二叉树
TreeNode* buildTree(int n) {
if (n == 0)
return NULL;
TreeNode* root = newTreeNode(0);
root->left = buildTree(n - 1);
root->right = buildTree(n - 1);
return root;
}
5.7 阶乘阶O(N!)
阶乘阶的算法复杂度最高,简直不会选用该类型的算法。
这是一个时刻复杂度为阶乘阶O(N!)的算法
int func(int n)
{
if (n == 0)
return 1;
int count = 0;
for (int i = 0; i < n; i )
{
count = func(n - 1);
}
return count;
}
示意图:
- 空间复杂度为阶乘阶O(N!)的算法并不常见,这里就不在一一列举。