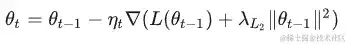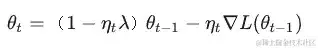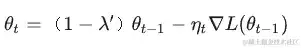导读

谈到 Weight Decay，必然咱们都不生疏，由于这是每位 AIer 每天都会用的计数，但却又是简直没人会关注的算法。

即便身处在以 ChatGPT 为代表所爆发的 LLM 年代，它仍是那么的有用，却又那么的朴实无华。

即便是在机器学习理论圈，研讨过 Weight Decay 机制的人也是少数派。

NeurIPS 2023 | 深入探讨 Weight Decay 的宿世此生和躲藏缺点

今日，为咱们介绍的是根据由东京大学等组织发表于 NeuraIPS 2023 的一篇文献 《On the Overlooked Pitfalls of Weight Decay and How to Mitigate Them: A Gradient-Norm Perspective》 所延伸开来的一篇关于经典算法——Weight Decay的讨论。

请注意，这不是一篇翻译文，而更多地是为了向咱们遍及知识，具体阐明完结这项作业的头绪。因而，请咱们耐性阅览，相信你们会从中取得一些启示和收获。

背景

在正式开始之前，我想很有必要回忆下权重衰减机制的来世此生。其实，现在咱们常说的 Weight Decay 至少有三种不同的方式。仅仅由于 Weight Decay 这个名词的滥用，咱们都在不同的场合被称作 Weight Decay，仅此而已。

No.1

第一种 Weight Decay，也便是当时 PyTorch/TensorFlow/Paddle 等深度学习结构里 optimizer 的默许 Weight Decay。简单点说，其实是L2 Regularization :)。在 SGD 里咱们能够将它写成下面这种方式：

NeurIPS 2023 | 深入探讨 Weight Decay 的宿世此生和躲藏缺点

L2 正则化很好了解，实际上是在原有的 loss 周围额定加多一个惩罚项。所以它的特色是，正则效果会先进入每一步迭代的梯度里，终究影响神经网络的参数。

No.2

第二种 Weight Decay，也便是当时大模型练习常用优化器 AdamW 里的 Decoupled Weight Decay。在 SGD 里能够写成下面这种方式：

NeurIPS 2023 | 深入探讨 Weight Decay 的宿世此生和躲藏缺点

这才是真实意义上的 decay weights，由于这儿每一步直接将权重以 1−nt1 – n_{t}lambda 因子衰减。

好吧，很容易看出来，关于 SGD 来说，上面两种方式是等价的。这也是为什么L2 Regularization会滥用Weight Decay这个姓名的原因:(

但更杂乱的优化器，比方 SGD Momentum 或 Adam，会使用动量（Momentum）和自适应学习率（Adaptive Learning Rate）等办法。这些实际上咱们最常用的优化器里，没有一个是能让上面两种方式正好等价的。

Adam （with L2 Regularization）和 AdamW （with Decoupled Weight Decay）这两个大模型练习最常用的两个优化器实际上只要 weight decay 的方式不同。可是他们的功能差异大到以至于分成了两个姓名不同的优化器。

那终究为什么会这样，详听下文讲解。

No.3

第二种 Weight Decay，也便是在练习神经网络时专门被提出来的原始 Weight Decay，来自一篇 1989 年的 NeurIPS 论文。在 SGD 里能够写成下面这种方式：

NeurIPS 2023 | 深入探讨 Weight Decay 的宿世此生和躲藏缺点

这是在做学习率解耦的 decay weights，每一步直接将权重以 1−′1-lambda^{prime} 因子衰减。

哪种更好呢？

看到这儿，或许咱们会有个疑问，上面说到了三种不同方式的权重衰减方式，那终究该用哪种呢？

其实，第三种 Weight Decay 是一种现已被筛选的方式。虽然深度学习结构的开发者们或许没有专门研讨过这个问题，但实际上其学习率解耦形式的确不如第二种方式。这是由于关于第三种 Weight Decay 来说，在学习衰减得比较小的练习晚期，Weight Decay 的强度总是太大了。咱们很容易在试验里观察到第三种 Weight Decay 的缺点。

而第一种的 L2 Regularization 依然在当时的深度学习结构流行；而第二种的 Decoupled Weight Decay 简直只在 Transformer 等架构盛行的 AdamW 等少量优化器里有官方实现。这个现状并欠好…

关于一些优化器，比方 SGD(Momentum)等，L2 Regularization 和 Decoupled Weight Decay 的功能并不是很大。但每逢 L2 Regularization 和 Decoupled Weight Decay 不同很大时，简直总是 Decoupled Weight Decay 明显地比 L2 Regularization 好。这简直发生在所有自适应优化器上。

所以<更好的原则是把 Decoupled Weight Decay 作为Weight Decay 的默许实现，把 L2 Regularization 作为备选。

说到这，挑刺的小伙伴或许又会说，既然这样，那 PyTorch/TensorFlow 等结构为啥直到今日仍是将 L2 正则化作为默许配置？此处盲猜或许是由于深度学习结构滥用名词 Weight Decay 指代 L2 Regularization 造成的一个前史遗留问题…

有啥躲藏缺点？

那么 Weight Decay 的故事就这么结束了吗？

不，上述论说仅仅个引子，目的便是为了点出当时权重衰减的缺点。

是的，哪怕是发展了这么多年的现已十分老练的 Weight Decay，其实还有挺严峻的躲藏缺点未被发现，这便是今日介绍的这个作业的首要奉献，下面让咱们一探终究！

不得不说，如果一个这么常用的算法还有严峻的缺点，那这个缺点的确藏得挺深。

这件事说起来也有点离谱。我第一次得到前文两个部分的 motivation 现已是3年前的事了。但深度学习理论的论文并不多了，所以一向也没有其他人把 Weight Decay 的这些特色说不清。关于第三种 Weight Decay 为什么比第二种 Weight Decay 差那么多，我一向没有得到一个比较完好的理论解释…

直到一个月黑风高的晚上，の，去年，终于有空搞点基础研讨，心血来潮做了一个试验，把 Gradient Norm 跟着练习进程的改变可视化出来。

经过观察 ResNet18 在 CIFAR-10 练习时的 Gradient Norm 曲线能够发现，Gradient Norm 会跟着 Weight Decay 的添加而明显添加。

好的。如果你有优化理论和泛化理论的基础，那么应该一下就能看出来 Weight Decay 它的确有点大毛病了！不必担心，我知道屏幕前的你看不懂，没关系，咱们持续… ^_^

这个试验其实呈现出一个违背传统认知的现象——Gradient Norm 竟然会跟着 Weight Decay 添加而明显添加！为什么这样说，由于这个现象至少从三个视点来说，都是和传统的了解是不相符的：

  1. 优化视点。Large Gradient Norms 阐明练习算法的收敛性变成很差，由于从某种意义上来说，gradient norm 的巨细便是收敛性最常见的指标。

  2. 泛化视点。Large Gradient Norms 阐明练习得到的权重泛化性很差，由于 gradient norm 的巨细也是泛化界常见的度量之一。

  3. 正则化视点。Large Gradient Norms 阐明练习得到的权重杂乱性变高了。而传统上，咱们以为 Weight Decay 是经过正则化效果来降低神经网络杂乱性，从而进步模型的泛化才能。而今日这试验的成果竟然正好相反，你说怪不怪？

因而，从这三个视点来说，Weight Decay 都大有问题。这也再次阐明，在深度学习里，许多传统了解都是很浅显的、适用范围狭窄的。当然，咱们都早已习惯做屌爆侠。

关于这三点，原文里供给了具体的剖析和参考文献，感兴趣的小伙伴能够去研读。

找到病因就好办了，由于接下来需要做的作业便是对症下药。于是，花了一天时间，终究把 Gradient Norm 的 Upper Bound 和 Lower Bound 都和 Weight Decay 强度正相关的理论证明了一下，算是把 Weight Decay 曩昔被忽略的关于 gradient norm 理论补全了。咱们理论也发现这些缺点在自适应优化器里尤为突出。这部分都是一个理论性论文里的程序性技术作业。

怎么对症下药？

本文作业设计了一个算法——Scheduled Weight Decay来弥补 Weight Decay 的上述缺点，也便是使用 Weight Decay 的时分，一起能够抑制 Gradient Norm。

这个办法思想上也很简单，便是当 Gradient Norm 太大的时分就让 Weight Decay 强度小一点，Gradient Norm 太小的时分就让 Weight Decay 强度大一点发挥效果。

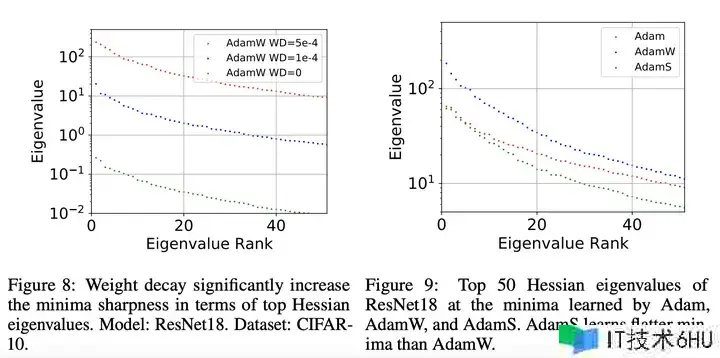
如下图8所示，所提优化算法 AdamS (Adam with Scheduled Weight Decay) 的确很好地完结了抑制 Gradient Norm 的效果。

NeurIPS 2023 | 深入探讨 Weight Decay 的宿世此生和躲藏缺点

能够看出，Scheduled Weight Decay 相比 Constant Weight Decay 明显降低练习晚期的 Gradient Norm!

一起，在上图9咱们还能看到，跟着 Weight Decay 添加时找到了更 sharp 的 minima（top Hessian eigenvalues 增大），这一般意味着泛化功能欠好。而 Scheduled Weight Decay 找到了比 Constant Weight Decay 更 flat 的 minima（top Hessian eigenvalues明显变小）。

一点浅显的剖析：

在深度学习中，Hessian 矩阵是丢失函数相关于模型参数的二阶导数矩阵。对 Hessian 矩阵进行特征值分化，得到的特征值中，top Hessian eigenvalues 表明最大的特征值。这些特征值供给了关于丢失曲面形状的信息。

此外，在练习神经网络时，找到丢失函数的极小值其实是一个优化问题。而 Sharp minima 便是丢失函数曲面上峻峭的最小值，而 flat minima 则是相对较陡峭的最小值。特征值的巨细和丢失曲面的形状有关，top Hessian eigenvalues 表明 Hessian 矩阵中最大的特征值，因而反映了曲面在该方向上的曲率。

上面咱们说到作者经过观察 top Hessian eigenvalues 跟着 Weight Decay 改变的趋势，能够得知丢失曲面的形状怎么随之改变。当 top Hessian eigenvalues 增大时，表明曲面更峻峭，这或许导致模型更容易陷入 sharp minima，而泛化功能或许较差。相反，当 top Hessian eigenvalues 变小时，表明曲面相对平整，模型更或许落入 flat minima，这或许对泛化功能更有利。因而，只需调整权重衰减的对应战略，使得 top Hessian eigenvalues 减小，便意味着找到的 minima 相对更 flat。这种调整是有助于改善模型的泛化功能。

一点言外之意

一些审稿人会把这个算法当作最首要的奉献，这阐明这部分审稿人始终是在从 Engineering 的视点来看待这个作业的。直白点说便是，他们以为 AI 仅仅一个黑盒机器，只要能 work 得更好，那便是研讨的悉数。

应用研讨的主（quan）要（bu）哲学——那的确便是 work 得更好就行。带实习生做 Neural Fields 方向的应用研讨最近半年也分别被 ICCV2023 和 ICLR2024，一投既中。只要功能好了，基本上就没有遇到过负分的审稿人。老实说，这种对功能的朴素寻求，的确有一点朴实无华…

说到这，或许大部分人都对“刷榜”疾恶如仇，但却又无可奈何，只能被逼着刷，打不过就换个视点刷，真实不行就换个方向再刷，(⊙﹏⊙)~~~

但包含作者在内的部分理论研讨者一般更乐意把 AI 当作一个客观的研讨目标。这种研讨视角能够叫做 Science of AI。包含 Sbastien Bubeck 在内的部分理论研讨者一般是把 AI 当作一个客观的研讨目标，也便是咱们首要是在做科学发现。偶尔，这些科学发现能促进更好的机器的诞生。微软AI理论研讨的带头人 Sbastien Bubeck 在他的主页在大模型的年代背景下更近一步把自己的研讨定位为Physics of AGI。

Sbastien Bubeck 主页：sbubeck.com/

研讨神经网络和研讨玻色爱因斯坦凝集不同真的很大吗？并不，他们肯定要服从某些真理。渐进低逼近真理便是新的科学。

咱们别的一篇 NeurIPS2023 其实也是科学发现型的论文，和一位物理系任教的朋友第一天讨论 idea 做试验，然后第二天就在神经网络里发现了咱们预言的试验成果。这种并不会出现在论文里的故事，能够留待下回写博客时介绍。

我个人觉得这篇文章最大的奉献其实是定位 Weight Decay 的躲藏缺点上，算法仅仅自然而然的副产品算了。这个作业也是在理论发现完结后马上被接收了，而不是在算法和试验的时分（很早就在Github上开源这个Weight Decay算法了）。而 Scheduled Weight Decay 也必然不是解决 Weight Decay 躲藏缺点的终究答案。由于它解决的是 Gradient Norm 的问题，而不是悉数的问题。Weight Decay 依然还有咱们不了解的问题。

Github: github.com/zeke-xie/st…

结束，感谢阅览。