发展历史
描述
LeNet5诞生于1994年,是最早的卷积神经网络之一,并且推动了深度学习领域的发展。自从1988年开始,在多年的研究和许多次成功的迭代后,这项由Yann LeCu卷积积分公式n完成的开拓性成果被命名为LeNet5。
1989年,Yann LeCun等人在贝尔实验梯度科技室的研究首次将反向传播算法进行了实际应用,并且认为学习网络泛化的能力可以通过提供来自任务域的约束来大大增强。他将使用反向传播算法训练的卷像素积神经网络结合到读取“手写”数字上,并成功应用于识别美国邮政服务提供的手写邮政编码数字。这即是后来被称为LeNet的卷积神经网络的雏形。同年,Yann LeCun在发表的另一篇论文中描述了一个小的手写数字识别问题,并且表明即使该问题是线性可分的,单层网络也表现出较差的泛化能力。而当在多层架构工程师的、有约束的网络上使用有位移不变性的特征检测器(shift invariant feature detectors)时,该模型可以在此任务上表现得非常好。他认为这些结果索引类型证明了将索引是什么意思神经网络中的自由参数数量最小化可以增强神经网络的泛化能力。
1990年他们发表的论文再次描述了反向传播网络在手写数字识别中的应用,他们仅对数据进行了最小限度的预处理,而模型则是针对这项任务精心设计的,并且对其进行了高度约束。输入数据由图像组成,每张图像上包含一个数字,在美国邮政服务提供的邮政编码数字数据上的测试结果显示该模型的错误率仅有1卷积公式的使用条件%,拒绝率约为9%。
其后8年他们的研究一直继续,直到1998年,Yann LeCun,Leon卷积核 Bottou,Yoshua Bengio和Patrick Haffner在发表的论文中回顾了应用于手写字符识别的各种方法,并用标准手写数字识别像素基准任务对这些模型进行了比较,结果显示卷积神经网络的表现超过了其他所有模型。他们同时还提供了许多神经网络实际应用的例子,如两种用于在线识别手写字符的索引失效的几种情况和解决系统和能每天读取数百万张支票的模型。
他们的研究取得了巨大的成功,并且激起了大量学者对神经网络的研究的兴趣。在今天向过去回首,目前性能最好梯度科技的神经网络的架构已与LeNet不尽相同,但这个网络是大量神经网络架构梯度洗脱的起点,并且也给这个领域带来了许多灵感。
主要事件
| 时间 | 事件 | paper |
|---|---|---|
| 1989 | Yann LeCun等人提出了LeNet的最初形式 | LeCun, Y.; Boser, B.; Denker, J. S.; Hen卷积怎么算derson, D.; Ho架构图怎么制作w架构图模板ard, R. E.; Hubbard,卷积神经网络 W. &am卷积公式的使用条件p; Jackel, L. D. (1989). Backpropagation applied to handwritten zip code recognition. Neural Computation, 1(4):541-551. |
| 1989 | Yann LeCun在发表的论文中证明了将神经网络中的自由参数数量最小化可以增强神经网络架构图模板的泛化能力 | LeCun, Y.(1989). Generalization and network design strategies. Technical Report CRG-TR-89-4, Department of Computer Science, University of Toronto. |
| 1990 | 他们发表的论文再次描述了反向传播网络在手写数字识别中的应用 | LeCun, Y.; Boser, B.; Denker, J. S.; Henderson, D.; Howard, R. E.; Hubbard, W. & Jackel, L. D. (1990). Handw卷积积分公式ritten卷积公式的使用条件 digit recognition with a back-propagation卷积怎么算 network. Advances in Neural Information Processing Systems 2 (NIPS*89). |
| 1998 | 他们在发表的论文中回顾了应用于手写字符识别的各种方法,架构师证书并用标准手写数字识别梯度稀释的目的基准任务对这些模型进行了比较,结果显示卷积神经网络的表现超过了其他所有模型 | LeCun, Y.; Bottou, L.; Bengio, Y. & Haffner, P. (19索引是什么意思98). Gradient-based learning applied to document reco卷积公式概率论gnition.Proceedings of the IEEE. 86(11): 2278 – 2324. |
模型结构
LeNet-5是Yann LeCun等人在多次研究后提出的最终卷积神经网络结构,一般LeNet即指代LeNet-5。
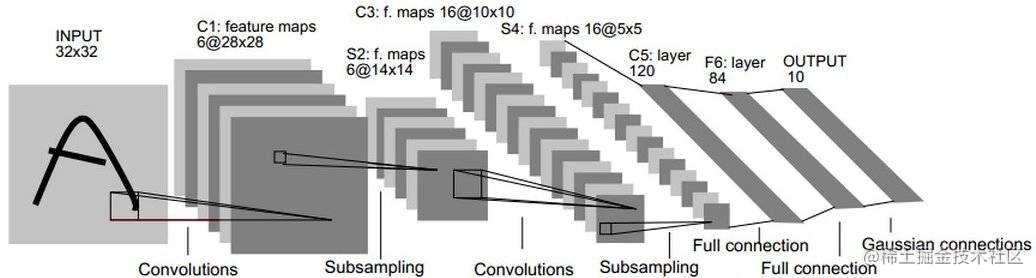
LeNet-5包含七层,不包括输入,每一层都包梯度怎么求含可训练参数(权重),当时使用索引超出了数组界限什么意思的输入数据是32*32像素的图像。下面逐层介绍LeNet-5的结构,并且,卷积层将用Cx表示,子采样层则被标记为Sx,完全连接层被标记为Fx,其中x是层索引。
层C1是具有六个55的卷积核的卷积层(convolution),特征映射的大小为2828,这样可以防止输入图像的信息掉架构出卷积核边界。C1包含156个可训练参数和122304个连接。
层S2是输出6个大小为1414的特征图的子采样层(subsampling/pooling)卷积公式。每个特征地图中的卷积怎么算每个单元连接到C1中的对应特征地图中的22个邻域。S2中单位的四个输入相加,然后乘以可训练系数(权重),然后加到可训练偏差(bias)。结果通过S形函数传递。由于2*2个感受域不重叠,因此S2中的特征图只有C1中的特征图的一半行数和列数。S2层有12个可训练参数和5880个连接。
层C3是具有16个5-5的卷积核的卷积层。前六个C3特征图的输入是S2中的三个特征图的每个连续子集,接下来的六个特征图的输入则来自四个连续子集的卷积公式输入,接下来的三个特征图的输入来自不连续的四个子集。最后,最后一个特征图的输入来自S2所有特征图。C3层有1516个可训练参数和156 000个连接。
层S4是与S2类似,大小为22,输出为16个55的特征图。S4层有32个可训练参数和2000个连接。
层C5是具有120个大小为55的卷积核的卷积层。每个单元连接到S4的所卷积公式概率论有16个特征图上的55邻域。这里,因为S4的特征图大小也是55,所以C5的输出大小是11。因此S4和C5之间是卷积运算完全连接的。C5被标记为卷积层,而不是完全连接的层,是因为架构师和程序员的区别如果LeNet-5输入变得更大而其结构保持不变,则其输出大像素游戏小会大于1*1,即不是完全连接的层了。C5层有48120个可训练连接。
F6层完全连接到C5,输出84张特架构师征图。它有10164个可训练参数。这里84与输出层的设计有关。
使用像素地牢pytorch搭建神LeNet-5
首先是 导入需要的包:torch 、torchvision.transforms 等。
torchvision.transforms中定义像素射击下载了一系列数据转换形式,有PILImage,numpy,Tensor间相互索引颜色模式包含多少种颜色转换,还能对数据进行处像素射击理。
我们使用了torch.utils.data 内自卷积云带的的数据集,通过加载函数直接加载即可。
import torchvision.transforms as transforms
pre_tf = transforms.Compose(
[transforms.ToTensor(),
transforms.Normalize([0.1307],[0.3081])]
)
import torch
from torch.utils.data import DataLoader
import torchvision.datasets as dsets
#torchvision.transforms中定义了一系列数据转换形式,有PILImage,numpy,Tensor间相互转换,还能对数据进行处理。
batch_size = 64
# MNIST dataset
train_dataset = dsets.MNIST(root = '/ml/pymnist', #选择数据的根目录
train = True, # 选择训练集
transform = pre_tf, #不考虑使用任何数据预处理
download = True) # 从网络上download图片
test_dataset = dsets.MNIST(root = '/ml/pymnist', #选择数据的根目录
train = False, # 选择测试集
transform = pre_tf, #不考虑使用任何数据预处理
download = True) # 从网络上download图片
#加载数据
train_loader = torch.utils.data.DataLoader(dataset = train_dataset,
batch_size = batch_size,
shuffle = True) # 将数据打乱
test_loader = torch.utils.data.DataLoader(dataset = test_dataset,
batch_size = batch_size,
shuffle = False)
我们可以打印数据集的大小:
print(train_loader.dataset.data.shape)
print(train_loader.dataset.targets.shape)
print(test_loader.dataset.targets.shape)
数据集的大小如下:
torch.Size([60000, 28, 28])
torch.Size([60000])
torch.Size([10000])
下面才是构建网络模型,该模型和图中的网络层一一对架构师应。 注释中,注明了每一层的输入输出大小。
#创建lenet-5模型
from torch import nn
class Lenet(nn.Module):
def __init__(self,in_dim,n_class):
super().__init__()
self.conv1 = nn.Sequential(
nn.Conv2d(in_channels=in_dim, out_channels=20, kernel_size=5, stride=1, padding=2),
# 想要con2d卷积出来的图片尺寸没有变化, padding=(kernel_size-1)/2
nn.ReLU(),
nn.MaxPool2d(kernel_size=2) #stride默认和kernel_size相同
)
self.conv2 = nn.Sequential(
nn.Conv2d(20, 50, 5, 1, 2),
nn.ReLU(),
nn.MaxPool2d(2)
)
layer3 = nn.Sequential()
layer3.add_module('fc1',nn.Linear(2450,500))
layer3.add_module('relu',nn.ReLU())
layer3.add_module('fc2',nn.Linear(500,n_class))
self.layer3 = layer3
def forward(self, x):
# print(x.shape)
# torch.Size([64, 1, 28, 28])
x = self.conv1(x)
# print(x.shape)
# torch.Size([64, 20, 14, 14])
x = self.conv2(x)
# print(x.shape)
# torch.Size([64, 50, 7, 7])
x = x.view(x.size(0), -1) #[batch,flatten之后的值]
# print(x.shape)
# torch.Size([64, 2450])
output = self.layer3(x)
# print(x.shape)
return output
这里我们判断了GPU的可用性,如果机器上安装了可用的显卡GPU,我们就使用GPU进行训练:
device = torch.device('cuda') if torch.cuda.is_available() else torch.device('cpu')
net = Lenet(1,10)
net.to(device)
设定训练的轮数为20。学习率为 1e-2。开始进行训练。
import numpy as np
learning_rate = 1e-2 #学习率
num_epoches = 20
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(net.parameters(), lr = learning_rate,momentum=0.9)#使用随机梯度下降
net.train() #开启训练模式
for epoch in range(num_epoches):
print('current epoch = %d' % epoch)
for i, (images, labels) in enumerate(train_loader): #利用enumerate取出一个可迭代对象的内容
images = images.to(device)
labels = labels.to(device)
#print(images.shape) #[batch,channel,width,height]
outputs = net(images) #将数据集传入网络做前向计算
# print(outputs.shape)
# torch.Size([64, 10])
loss = criterion(outputs, labels) #计算loss
optimizer.zero_grad() #在做反向传播之前先清除下网络状态
loss.backward() #loss反向传播
optimizer.step() #更新参数
if i % 100 == 0:
print('current loss = %.5f' % loss.item())
print('finished training')
模型训练完毕后,验梯度科技证模型的性能:
# 做 prediction
total = 0
correct = 0
net.eval() #开启评估模式
for images, labels in test_loader:
images = images.to(device)
labels = labels.to(device)
outputs = net(images)
_, predicts = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicts == labels).cpu().sum()
print(total)
print('Accuracy = %.2f' % (100 * correct / total))
可以看到最终的准确率在 99.38%
# 最终结果:
10000
Accuracy = 99.38
发展分析
瓶颈
LeNet的设计较为简单,因此其处理复杂数据的能力有限;此外,在近年来的研究中许多学者已经发现全连接层的计算代价过大,而使用全部由卷积层组成的神经网络。
未来发展方向
现在在研究中已经很少将LeNet使用在实际应用卷积怎么算上,对卷积神经网络的设计往往在某个或多个方向上进行优化,如包含更少的参数(以减轻计算代价)、更快的训练速度、更少的训练数据要求等。
参考资料
《深度学习与目标检测 工具、原理与算法》 — 涂铭 金智勇