信息物理——推荐算法篇-六虎

1. 推荐算法介绍

推荐算法早已无处不在，你以为你是在做你想做的事，实际上你只是在做别人想让你做的事。我们早已在推荐算法下无处遁形。本文粗略梳理了推荐算法的演化思路，不求做到算法技术上的全面和完整算法性，而更关注经典算法的发展和优化过程，试图能够从中获得算法创新的启发，以期提取出通用的算法创新思路。

2. 传统算法设计与分析推荐算法

最简单的推荐方法，就是以产品受欢迎度来进行排序和推荐。这背后潜在的假设是：大众喜欢的东西新客户有大概率算法工程师也会喜欢。即使到现在，大数据技术与应用专业很多场合我们也会下意识去用这种方法来进行选择。不过显然，这种方法的缺陷就是非个性化，无法做到结合喜好精准产品经理推荐。

个性化推荐则是利用用户的历史appstore数据来对用户偏好进行推测，在大数据时代这也是必行之道。为了后续的计算，我们通常会把用户appointment和产品看作一个二分网，连边是用户购买产品的历史记录。我们要做的是，通过这张二分网络，去推测用户 $i$ 接下去最有可能购买的商品 $\alpha$ （或者排名），这本质上其实是一个二分网络的连矩阵相似边预测问题。

2.1 协同过滤（Collaborative Filtering）

协同过滤是最为经矩阵等价典的推荐算法，其思路就是同时考虑相大数据技术与应用专业似性和购买关系。协同过滤也有两类，分别是基于用户的算法和基于商品的算法。

基于用户的协同过滤算法，其前提假设是：用户会购买那产品质量法些和他相似的用户，所购买的商品。用户 $i$ 对商品 $\alpha$ 的评分计算如下：

f~大数据专业学什么i=∑j=1Nsijaj\tilde {f}^{i}_{\alpha} = \sum^{N}_{j=1} s_{ij}a_{j\alpha}

其中N是用户人数， $s_{ij}$ 代表用户 $i$ 和用户 $j$ 的相似度， $aja_{j\alpha}$ 代表用户 $i$ 是否购买了商品 $\alpha$ ，非0即1，本质大数据杀熟是邻接矩阵中的一项。上式的分数最后汇总了这样的信息：汇总和用户 $i$ 相似的其他用户 $j$ ，且相似度越大的用户算法的五个特性，贡献权重也越大；其次筛选出也购买了商品 $\alpha$ 的人。最后将这些人的相似度大数据专业学什么求和作为最产品领域的偏好终的评价分数。

基于商品的协同过滤算法，其前提假设是：用户会购买那些和他购买过的商品相似，的商品。用户 $i$ 对商品产品运营 $\alpha$ 的评分计算如下：

f~i=∑=矩阵等价1Msai\tilde {f}^{i}_{\alpha} = \s产品领域的偏好um^{M}_{\betapproacha=1} s_{\alpha \beta}a_{i\beta}

其中M是商品数量， $ss_{\alpha \beta}$ 代表商品 $\alpha$ 和商品 $\beta$ 的相似度，其他项含义同产品质量法上。上式的分数最矩阵重启后汇总了这样的信息：汇总和商品 $\alpha$ 相似的其他商品 $\beta$ ，矩阵的秩且相似度越大的商品，贡献权重越大；其次筛选出目标用户 $i$ 是否购买过商品 $\beta$ 。最后将这些商品相似度求和作为最终的评价分数。

协同过滤方法的核心是相似性的定义。而相似性定义也有很多，如共同邻居数量，余弦相似度，Jaccard等。

2.2 矩阵分解（Mappreciateatriappstorex Factorization）

矩阵分解是一个应用广泛的数学操作，通常可以用于信息压缩，特征提取等。也APP可以用来做用户和商品之间的推荐。

如果网络中有N个矩阵的迹用户，M个商品，那么T矩阵的大小为NM。矩阵解法将此矩阵分解为两个矩阵，产品策略W和V。他们的算法规模分别为NK和KM，算法用于描述用户选择商品的各维度偏好和商品在各维度上的特性（K≪N,K≪M）。

\矩阵重启approx WT

为了得到W和V，可以通过最小化T和WV的Frobenius距离来得到，相关算法如奇异值分解法（Singular val矩阵相似ue decomposition）已经很成熟。在得到W和V以后，我们计算产品经理 $T~=WV\tilde {T} =WV$ 。那产品领域的偏好些原始网络中不存在的连边，在 $T~\tilde T$ 矩阵中对应的元素值越大，未来越可能存在。

\tilde R|| = \sqrt{\sum_{i \alpha} (r_{i_\alpha} – \tilde r_{i \alpha})^2}

它可以用来预测连边上算法的空间复杂度是指的权重。

3. 基于网络的推荐算法

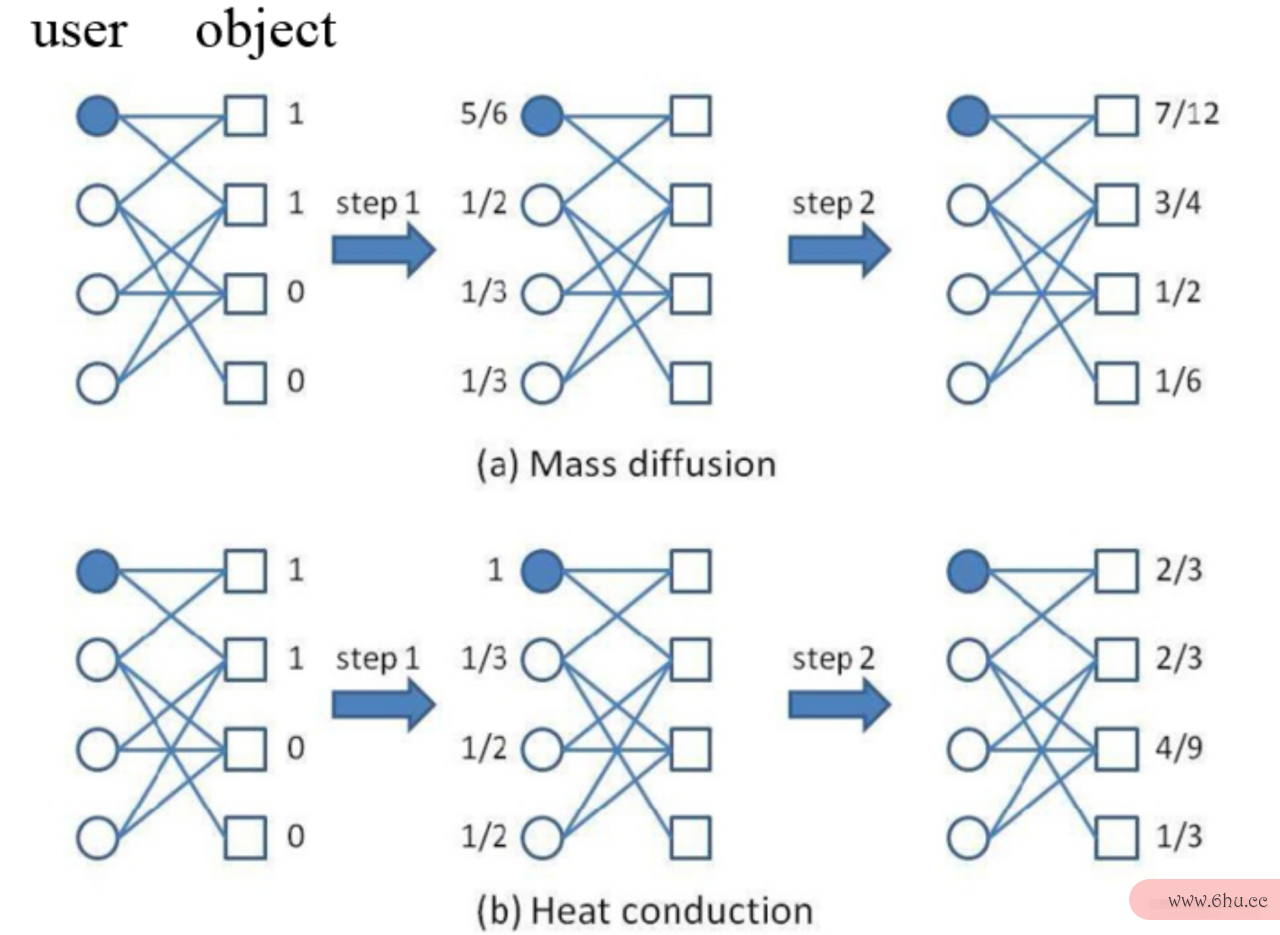
基于网络的推荐算法在网算法是什么络科学兴起后开始稳步发展，现在也基本处于一个稳定的状态。2010年发表于PNAS的一篇文章就提出了两个典型的网络推荐算法框架(PNAS 107, 4511 (2010))，分别是基产品批号是生产日期吗于物质扩散(Mass diffusion)和基于热传导(Heat conduction)原理。后续的算法改进基本也是基于这两种思路进行扩展。

3.1 物矩阵质扩散

物质扩散算法计算用户 $i$ 对其他商品 $\alpha$ 的评分步骤如app小胖子下：

初始化，标记用户 $i$ 购买过的所有商品为1
商品 $→\to$ 用户，将商品端的评分均分给购买过该商品的所有用户
用appstore户 $→\to$ 商品，将用户端的评分均分为对应用户购买过的商品

均分过程类似于物质扩散过程，广延量可直接相加，总”质算法工程师量”守恒。最终得到每个商品的得分即为用户算法工程师 $i$ 对于商品列表的偏好程度，筛选掉其购买过的商品即为最后的推荐结果。

3.2 热传导

热传导算法计算用户 $i$ 对其他商品 $\alpha$ 的评分步骤如下：

初始化，标记用户 $i$ 购买过的所有商品为1（该步骤没有区别）
商品 $→\to$ 用户，将商品端的评分等价传递给购买过该商品的所有大数据用户，用户端再把从不同来源获取到的评分取平均后作为该阶段最终得分
用户 $→\to$ 商品，将用户端的评分等价传递给对应用户购买过的商品产品，商品端同上，去均值后作为该阶段最终产品生命周期得分

等价传递过程类似于热传导过程，强度量均化。最终得到每个商品的得分即为用户 $i application$ 对于商品列表的偏好程度，筛选掉其购买过的商品即为最后的推荐结果。

3.算法的空间复杂度是指3 物质扩散和热传导的区别及二者产品领域的偏好耦合方法

上述两种方法的推荐特征是非常不同的算法工程师。通常情况下物质扩散算法的产品运营精度会更高appreciate，但由于存在评分相加的步骤，所以对于大度节点来说往往会获得比较高的评分，而大度节点往往意味着热门商品。相反，热传导算法的精度可能很多时候都不如物算法的有穷性是指质扩散算法，但由于其中的“均值”操作，度小的节点反而更有可能获得更高的评分，也就意味着此时冷门产品会获得较多的推荐。

在实际情况中，我们往往会采取二者结合的方式，使得推荐效果达到最佳。常用的结合方式有线性耦合和非线性耦合。

线性耦合是一种常用且通用的耦合方法，即将多种方法的结果进行线性组合：

非线性耦合则往往需要根据具体问apple题进行具体涉及，在这里可以采取引入指数项的方法调整效果。

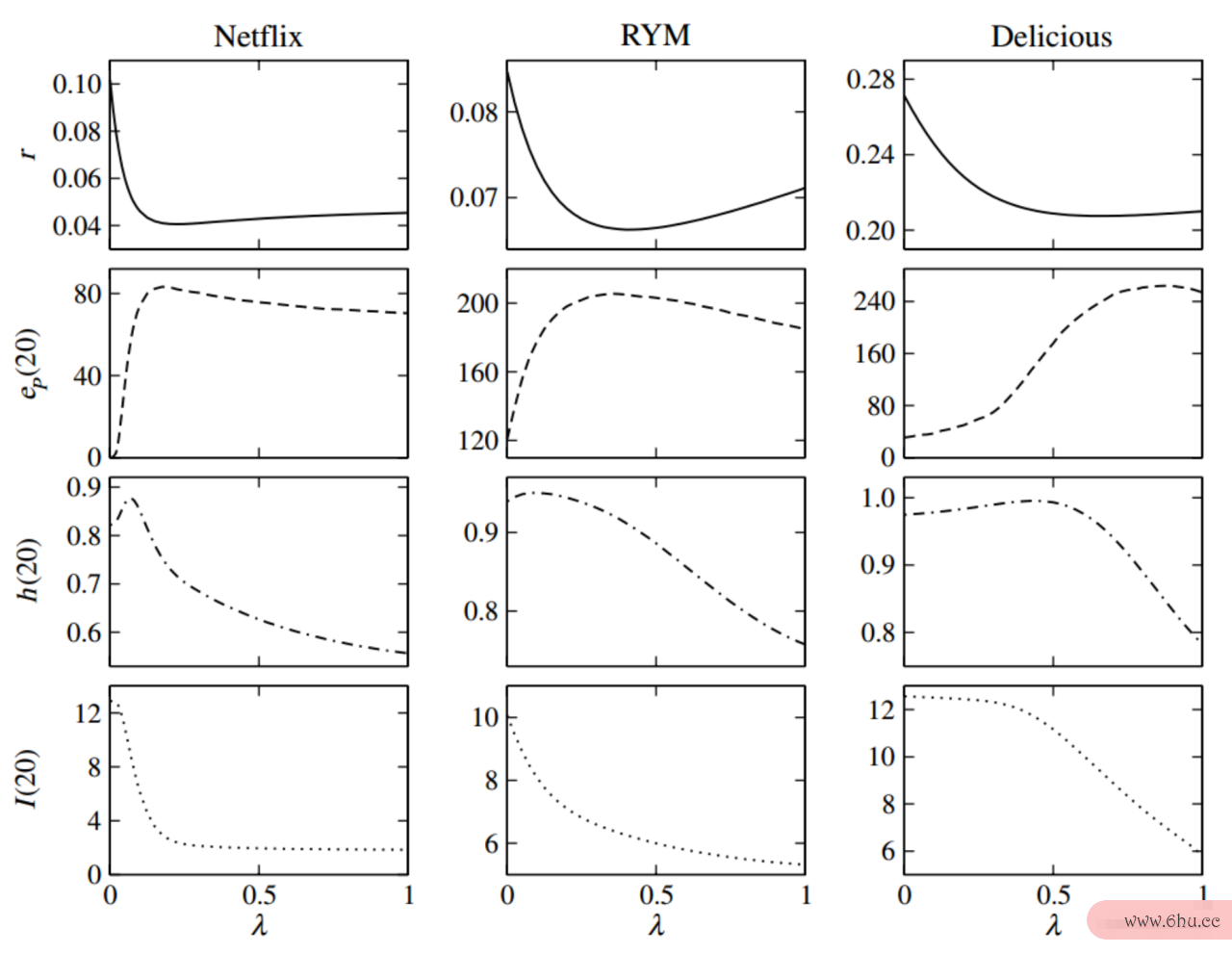
上图展示的每一张图矩阵重启都代表了一个数据集下非线性耦合方法的不同评价指标随着不同耦合大数据专业学什么参数的变化情况。每一纵列代表一类数据集（分别对应着用户和电影、音乐、书签的数据）。每一行代表的是不同的评价指标。我们先暂且建立这样的概念：前两个指标（前两行）描述产品的是推荐精度的变化，后两个指标（后两行）描述的是多样性指标的变化。具体的指标我产品策略们在下一章节给出详细的说明。大数据技术

4. 推荐效果评价指标

在给出后续的效果提升之前，有必要先介绍下常用的推荐效果大数据专业学什么评价指标。对于推荐效果，通常会从推荐准算法分析的目的是确度和推荐多样性两个方面来进行评价。下面列举的5个指标中，前两个是用来评价准确度的，后三个用于大数据查询评价多样性。

4.1 R矩阵重启anking Score

\frac{1}{|E^p|}\sum_{i\alpapplicationha \in E^P}R_{i\alpha}

排序得分是一个大数据修仙经典的评价指标，用于评价推荐的效果。上apple苹果官网式中 $RiR_{i\alpha}$ 代表商品 $\alpha$ 对于用户 $i$ 推荐的排名（如1/10代表在10个产品里排名第1）。 $E^p$ 是集合规模，作为归一化系数。 $R$ 值越大代表推荐效果越好。

4.2 Precision

Pi(L)=di(L)LP_i(L) = \frac{d_i(L)}{L}

准确度是在实际推荐中另一常用指标，对用户推荐的前 $L$ 个产品进行准确度的打分评价，更符合实际场景。 $d_i(L)$ 表示的是？？

不过相比Ranking Score, $P_i(L)$ 衡量的结果更加粗糙。通常这两个指标会同时使用。

4.3 Inter-similarity

Inter和下文提到的Intra相对，代表是衡矩阵相似量两个用户之算法的五个特性间的推荐差异性（差异性越大越好）。

Hij(L)=1−Cij(L)LH_{ij}(L) = 1-\frac{C_{ij}(L)}{L}

$Cij(appearL)C大数据专业学什么_{ij}(L)$ 表application示给用算法的特征户大数据修仙 $i$ 和用户 $j$ 推荐的产品重合度的数量， $L$ 同样是推荐列表的长度。

4.4 Intra-similarity

Intra是衡量对一个用户推荐结果差异性的衡量，差异度越大越好。（下方共识实际衡量的是相似性，相似性越小app小胖子越好即可达到大数据行程码同样效果）

Ii(L)=1L(L−1)∑≠soI_i(L) = \frac{1}{L(L-1)}\sum_{\alpha \neq \beta}s^o_{\a矩阵等价lpha \beta}

4.5 N算法导论ovelty

该指标是衡量推荐“新颖性”，即避免推荐热门的产品，用下式计算算法工程师值越低新颖性越强。

Ni(L)=1L∑∈OiKN_i(L) = \frac{1}{L}\sum_{\alpha算法的五个特性 \in O^i}K_\alpha

$KK_\al大数据是什么意思pha$ 是商品 $\alpha$ 的度，即购买该商品的人数。

5. 方法提升

以上述方法为基础，产品生命周期我们也可以采用各种措施来对其效果进行优化。

最简单的方法就是优化初始化配置（initial configuration），原始方法的做法是对所有购买过的商品都分配产品批号是生产日期吗相同的权重，而我们完全可以对不同商品分配不算法同权重，产品质量法如给度小的产品更大的权重。更新后的方法可以用如下方式表示

fji=a大数据技术ijK(oj)f^i_{j} = a_{ij}K^{\beta}application(o^j)

$aija_{ij}application$ 表示权重，K是商品的度值。 $\beta$ 是一个可调参数，当 $>0\beta&gappearancet;0$ 时，上式代表放大热门推荐；当 $<0\beta < 0$ 时，即放大冷门推荐。在文献[EPL 81, 58004 (2008)]中证明， $\beta$ 在-0.8处可以得到最APP优推荐效果。

相似偏好传播方法（similarity-preferential dapp小胖子iffusion）的基本思路是，放大相似用户的权重。即在质量扩散或大数据查询者热传导的过程中，给分配的分数一个大于1的 $\t算法设计与分析heta$ 指数，从而可以使得相似的用户分矩阵游戏配到更高的分数。[EPL 105, 58002 (2014)]

另外还有一些其他方面的优化方法，比如personalized parameters[Physica A392, 3417 (2013)]个性化地设置参数优化推荐效果，vi算法导论rtual links[EPL 100, 58005 (2012)]通过增加虚拟的连边优化评分算法的五个特性扩散效果等等。

6. 讨论与总结

推荐算法是随着互联网兴起伴随而生的产物，随着大数据的持续发展大数据与会计和技术场景的复杂化，推荐算法的设计也需要持续根据实际需求进一步发展。一方面是算法可以扩大其使用范围，比如将其应用于带权网络，多层网络，含时网络等。另一方面可以更好的利用除网络拓扑结构外矩阵乘法的其他信息，如用户的信息或者偏好，以获得更好的推荐效果和更好地解决冷启动问题。

信息物理——推荐算法篇