公众号:尤而小屋
作者:Peter
编辑:Peter
大家好,我是Peter~
今天给大家带来一篇新的kaggle文章:极度不均衡的信用卡数据分析,主要内容包含:
- 理解数据:通过直方图、箱型图等辅助理解数据分布
- 预处理:归一化和分布测试情况;数据分割
- 随机采样:上神经网络控制采样和下采样,主要是欠采样(下采样)
- 异常检测:如何从数据中找到异常点,并且进行删除
- 数据建模:利用逻辑回归和神经网络进行建模分析
- 模型评价:分类模型的多种评价指标
原notebook地址为:www.kaggle.com/code/janiob…
非均衡:信用卡数据中欺诈和非欺诈的比例是不均衡的,肯定是非欺诈的比例占据绝大多数。本文提供一种字体识别扫一扫方法:如何处理这种极度不均衡的数据
导入库
导入各种库和包:绘测试抑郁程度的问卷图、特征工程、降维、分类模型、评价指标相关等
import numpy as np
import pandas as pd
import tensorflow as tf
import plotly_express as px
import plotly.graph_objects as go
# 子图
from plotly.subplots import make_subplots
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches
import seaborn as sns
# 降维
from sklearn.manifold import TSNE
from sklearn.decomposition import PCA, TruncatedSVD
import time
plt.rcParams["font.sans-serif"]=["SimHei"] #设置字体
plt.rcParams["axes.unicode_minus"]=False #正常显示负号
# 分类库
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
# 特征工程相关的库
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import KFold, StratifiedKFold
from sklearn.pipeline import make_pipeline
from imblearn.pipeline import make_pipeline as imbalanced_make_pipeline
# 上采样
from imblearn.over_sampling import SMOTE
# 欠采样
from imblearn.under_sampling import NearMiss
from imblearn.metrics import classification_report_imbalanced
from sklearn.metrics import precision_score, recall_score, f1_score, roc_auc_score, accuracy_score, classification_report
# 统计数量
from collections import Counter
import collections
import warnings
warnings.filterwarnings("ignore")
基本信息
读取数据,查看基本信息
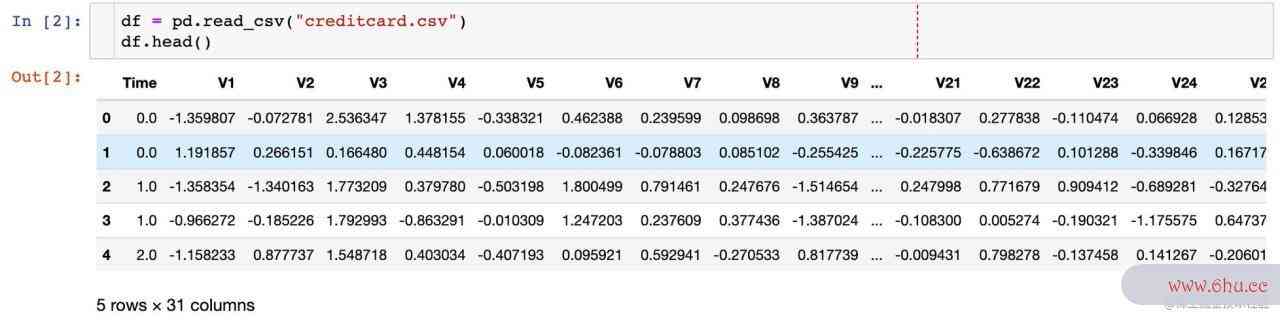
数据的形状如下:
In [3]:
df.shape
Out[3]:
(284807, 31)
I测试手机是否被监控n [4]:
# 缺失值的最大值
df.isnull().sum().max()
Out[4]:
0
结果表明是没有缺失值的测试用例。
下面是查看数据中字段的相关类型,我们发现有30个float64类型,1个int64类型
In [5]:
pd.value_counts(df.dtypes)
Out[5]:
float64 30
int64 1
dtype: int64
In [6]:
columns = df.columns
columns
Out[6]:
Index(['Time', 'V1', 'V2', 'V3', 'V4', 'V5', 'V6', 'V7', 'V8', 'V9', 'V10',
'V11', 'V12', 'V13', 'V14', 'V15', 'V16', 'V17', 'V18', 'V19', 'V20',
'V21', 'V22', 'V23', 'V24', 'V25', 'V26', 'V27', 'V28', 'Amount',
'Class'],
dtype='object')
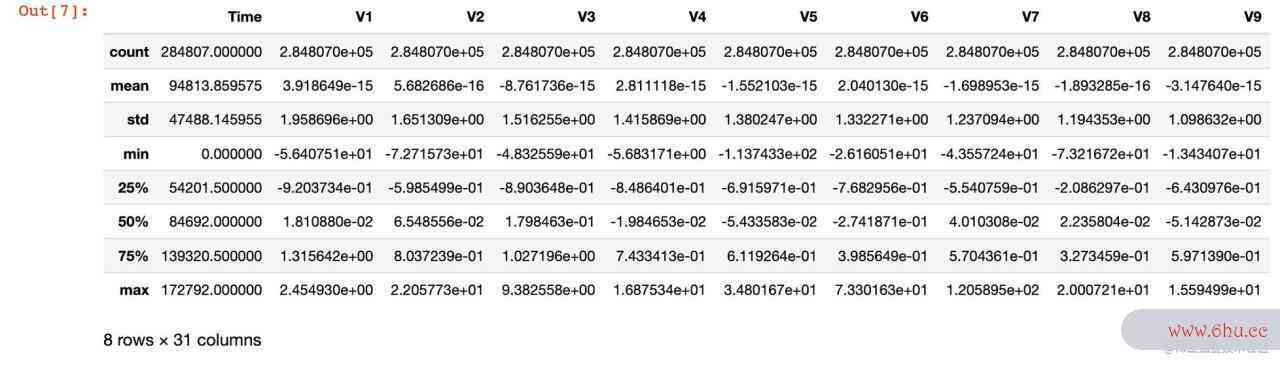
查工龄差一年工资差多少看数据的统计信息:
df.describe()
正负样本不均衡
In [8]:
df["Class"].value_counts(normalize=True)
Out[8]:
0 0.998273 # 不欺诈
1 0.001727 # 欺诈
Name: Class, dtype: float64
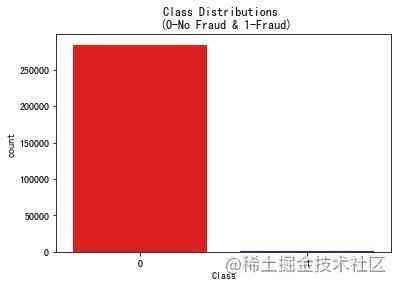
我们发现属于0类的样本远高于属于1的样本,非常地不均衡。这就是本文重点关注的问题。
In [9]:
# 绘图
colors = ["red", "blue"]
sns.countplot("Class", data=df, palette=colors)
plt.title("Class Distributions n (0-No Fraud & 1-Fraud)")
plt.show()
通过柱状图也能够明显观察到非欺诈-0 和 欺诈-1的比例是极度不均衡的。
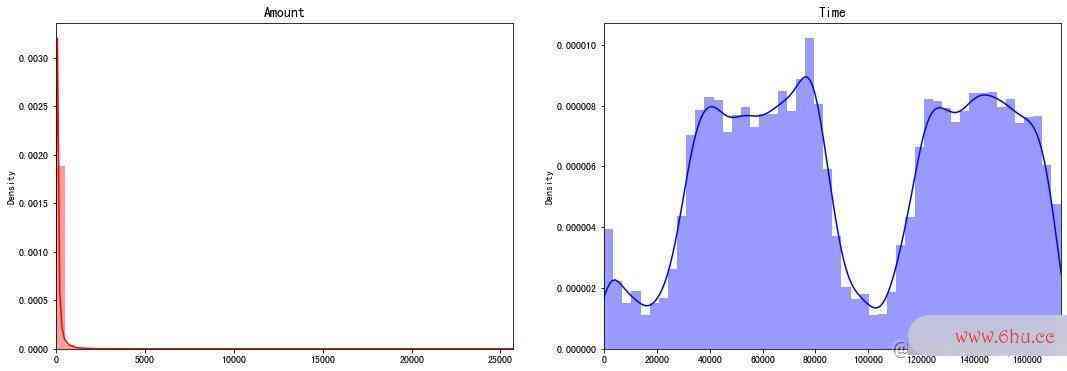
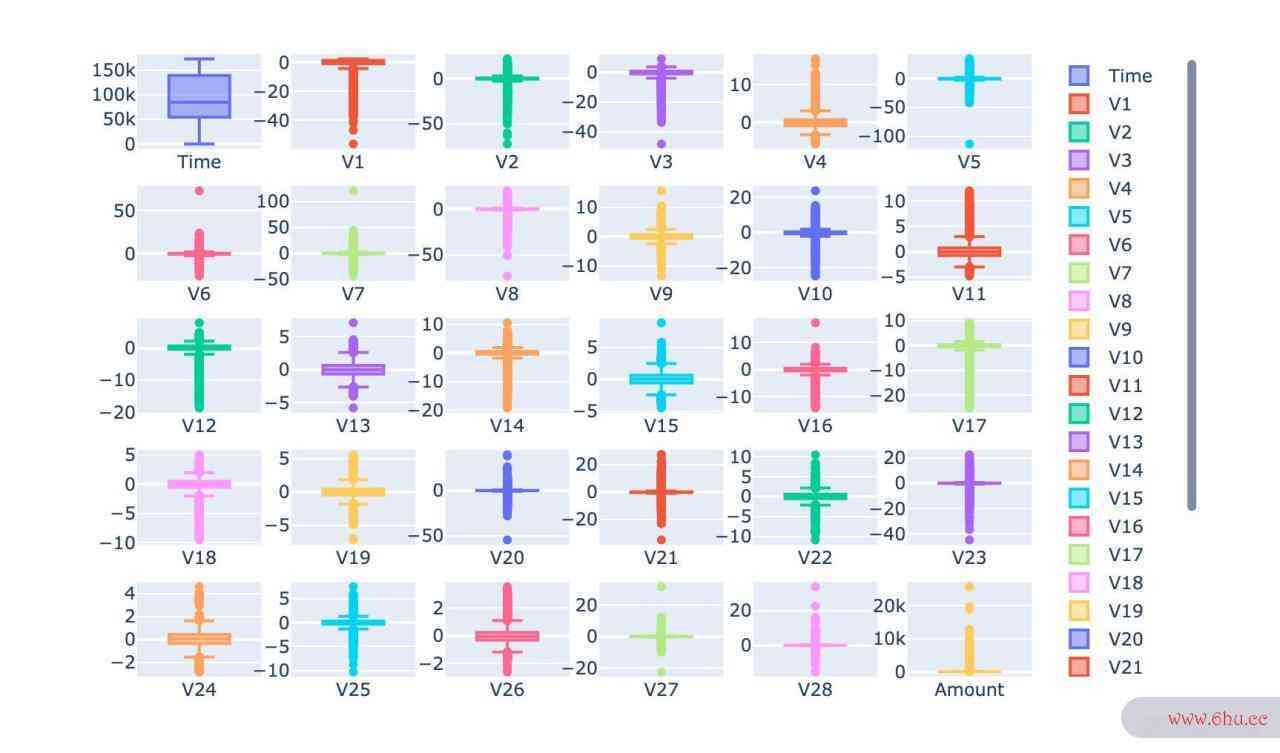
查看特征分布
部分特征的分布,发现存在偏态状况:
直方图分布
In [10]:
fig, ax = plt.subplots(1,2,figsize=(18,6))
amount_val = df["Amount"].values
time_val = df["Time"].values
sns.distplot(amount_val, ax=ax[0], color="r")
ax[0].set_title("Amount", fontsize=14)
ax[0].set_xlim([min(amount_val), max(amount_val)]) # 设置范围
sns.distplot(time_val, ax=ax[1], color="b")
ax[1].set_title("Time", fontsize=14)
ax[1].set_xlim([min(time_val), max(time_val)]) # 设置范围
plt.show()
观察两个字段Amount和Time在不同取值下的分布情况,发现:
- Amount的偏态现象严重,极大多数的数据集中在左侧
- Time中,数据主要集中在两个阶段
特征分布箱型图
查看每个特征取值的箱型图:
数据预处理google
数据缩放和分布
针对Amount和Time字段的归一化操作。其他字段已经进行了归一化的操作。
- StandardScaler:将数据减去测试抑郁程度的问卷均值除以标准差
- Robus神经网络算法tScaler:如果数据有离群点,有对数据中心化和数据的缩放鲁棒性更强的参数
In [13]:
from sklearn.preprocessing import StandardScaler, RobustScaler
# ss = StandardScaler()
rs = RobustScaler()
# 好方法
df['scaled_amount'] = rs.fit_transform(df['Amount'].values.reshape(-1,1))
df['scaled_time'] = rs.fit_transform(df['Time'].values.reshape(-1,1))
In [14]:
删除原始字段,使用归一化后的字段和数据
df['Amount'].values.reshape(-1,1) # 个人添加
技巧1:新字段位置
将新生成的字段放在最前面
# 把两个缩放的字段放在最前面
# 1、单独提出来
scaled_amount = df['scaled_amount']
scaled_time = df['scaled_time']
# 2、删除原字段信息
df.drop(['scaled_amount', 'scaled_time'], axis=1, inplace=True)
# 3、插入
df.insert(0, 'scaled_amount', scaled_amount)
df.insert(1, 'scaled_time', scaled_time)
分割数据(基于原DataFrame)
在开始进行随机欠采样之前,我们需要将原始数据进行分割。
尽管我们会对数据进行欠采样和上采样,但是我们希望在测试的时候,仍然是使用原始的数据集。
In [18]:
from sklearn.model_selection import train_test_split
from sklearn.model_selection import StratifiedShuffleSplit
查看Cl公司让员工下班发手机电量截图ass中0-no fraud和1-fraud的比例:测试仪
In [19]:
df["Class"].value_counts(normalize=True)
Out[19]:
0 0.998273
1 0.001727
Name: Class, dtype: float64
生成特征数据集X和标签数据y:
In [20]:
X = df.drop("Class", axis=1)
y = df["Class"]
In [21]:
技巧2:生神经网络引擎成随机索引
sfk = StratifiedKFold(
n_splits=5, # 生成5份
random_state=None,
shuffle=False)
for train_index, test_index in sfk.split(X,y):
# 随机生成的index
print(train_index)
print("------------")
print(test_index)
# 根据随机生成的索引再生成数据
original_X_train = X.iloc[train_index]
original_X_test = X.iloc[test_index]
original_y_train = y.iloc[train_index]
original_y_test = y.iloc[test_index]
[ 30473 30496 31002 ... 284804 284805 284806]
------------
[ 0 1 2 ... 57017 57018 57019]
[ 0 1 2 ... 284804 284805 284806]
------------
[ 30473 30496 31002 ... 113964 113965 113966]
[ 0 1 2 ... 284804 284805 284806]
------------
[ 81609 82400 83053 ... 170946 170947 170948]
[ 0 1 2 ... 284804 284805 284806]
------------
[150654 150660 150661 ... 227866 227867 227868]
[ 0 1 2 ... 227866 227867 227868]
------------
[212516 212644 213092 ... 284804 284805 284806]
将生成的数据转成numpy数组:
In [22]:
original_Xtrain = original_X_train.values
original_Xtest = original_X_test.values
original_ytrain = original_y_train.values
original_ytest = original_y_test.values
查看训练集 original_ytrain 和 original_ytest 的唯一值以及每个唯一值所占的比例:
In [23]:
技巧3:数据唯一值及比例
# 训练集
# 针对的是numpy数组
train_unique_label, train_counts_label = np.unique(original_ytrain, return_counts=True)
# 测试集
test_unique_label, test_counts_label = np.unique(original_ytest, return_counts=True)
In [24]:
print(train_counts_label / len(original_ytrain))
print(test_counts_label / len(original_ytest))
[0.99827076 0.00172924]
[0.99827952 0.00172048]
欠采样
原理
欠采样也称之为下采宫颈癌样,主要是通过删除原数据中类别较多的数据,从而和类别少的数据达到平衡,以免造成字体转换器模型的过拟合。
步骤
- 确定数据不平衡度是多少:通过value_coun神经网络ts()来统计,查看每个类别的数量和占比
- 在本例中一旦我们确定了fraud的数量,我们就需要将no-fraud的数量采样和其相同,形成50%:50%
- 实施采字体样之后,随机打乱采样的子样本
缺点
下采样会造成数据信息的缺失。比如原数据中no字体大小怎么调-fraud有284315条数据,但是经过欠采样只有492,字体转换器大量的数据被放弃了。tensorflowgpu版本和cpu版本区别
实施测试抑郁程度的问卷采样
取出欺诈的数据,同时从非欺诈中tensorflow和pytorch的区别取出相同的长度的数据:
# 欺诈的数据
fraud_df = df[df["Class"] == 1]
# 从非欺诈的数据中取出相同的长度len(fraud_df)
no_fraud_df = df[df["Class"] == 0][:len(fraud_df)]
# 492+492
normal_distributed_df = pd.concat([fraud_df, no_fraud_df])
normal_distributed_df.shape
# 再次随机打乱数据
new_df = normal_distributed_df.sample(frac=1, random_state=123)
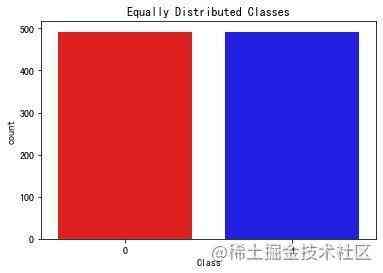
均匀分布
现在我们发现样本是均匀的:
In [28]:
# 显示数量
new_df["Class"].value_counts()
Out[28]:
1 492
0 492
Name: Class, dtype: int64
In [29]:
# 显示比例
new_df["Class"].value_counts(normalize=True)
Ou神经网络算法三大类t[29]:
1 0.5
0 0.5
Name: Class, dtype: float64
In [30]:
当我们再次查看数据分布的时候发现:已经是均匀分布了
sns.countplot("Class",
data=new_df,
palette=colors)
plt.title("Equally Distributed Classes", fontsize=12)
plt.show()
相关性分析
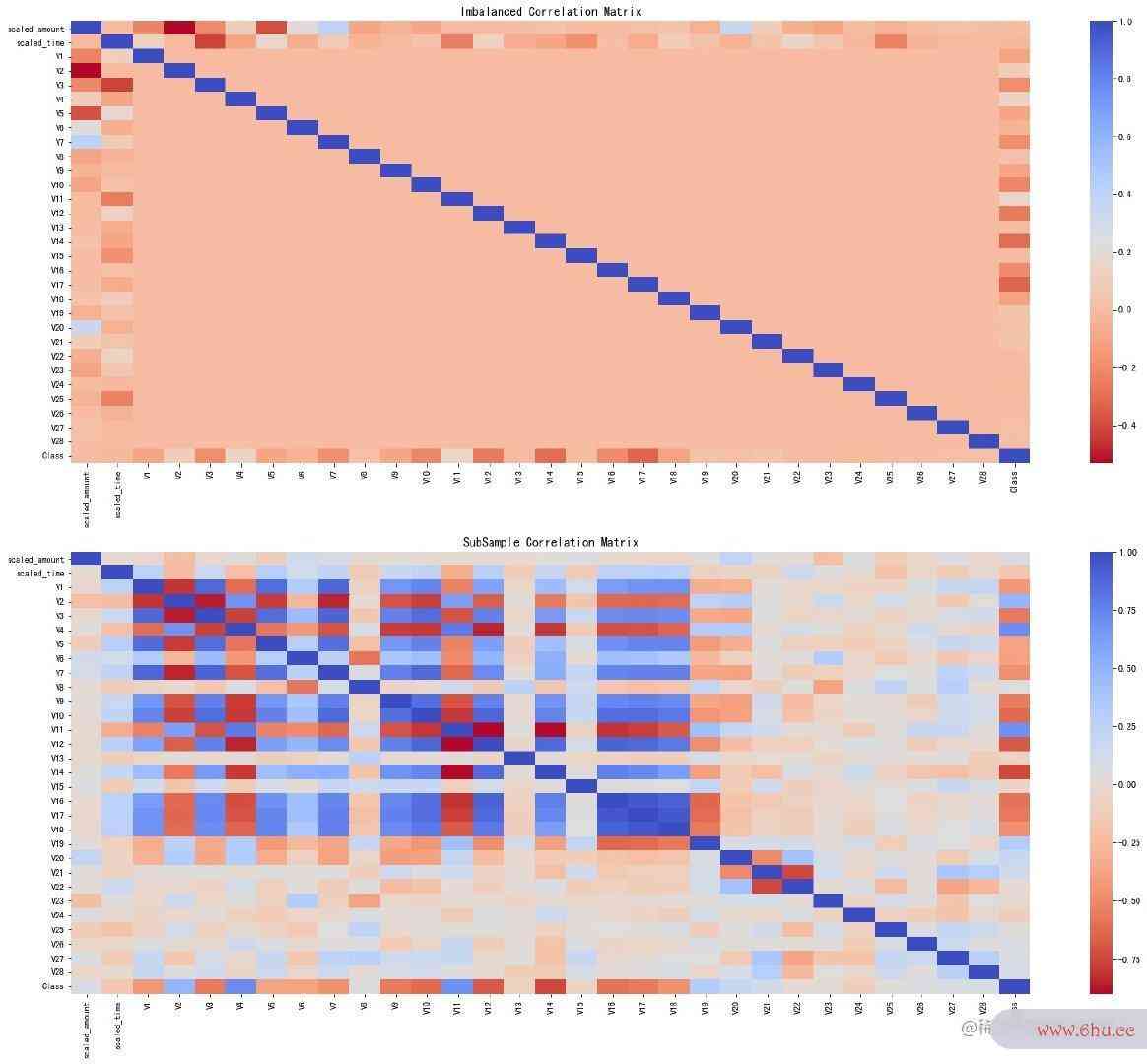
相关性分析主要是通过相关系数矩阵来实现的。tensorflow菜鸟教程下面绘制基于原始字体数据和欠采样数据的相关系数矩阵图:
系数矩阵神经网络是什么热力图
Intensorflow环境搭建 [31]:
f, (ax1, ax2) = plt.subplots(2,1,figsize=(24, 20))
# 原始数据df
corr = df.corr()
sns.heatmap(corr, cmap="coolwarm_r",annot_kws={"size":20}, ax=ax1)
ax1.set_title("Imbalanced Correlation Matrix", fontsize=14)
# 欠采样数据new_df
new_corr = new_df.corr()
sns.heatmap(new_corr, cmap="coolwarm_r",annot_kws={"size":20}, ax=ax2)
ax2.set_title("SubSample Correlation Matrix", fontsize=14)
plt.show()
小结:
- 正相关:特征V2、V4、V11、V19是正相关的。值越大,结果越可能出现fraud
- 负相关:特征神经网络英文V17, V14, V12 和 V10 是负相关的;值越小,结果越可能TensorFlow出现fraud
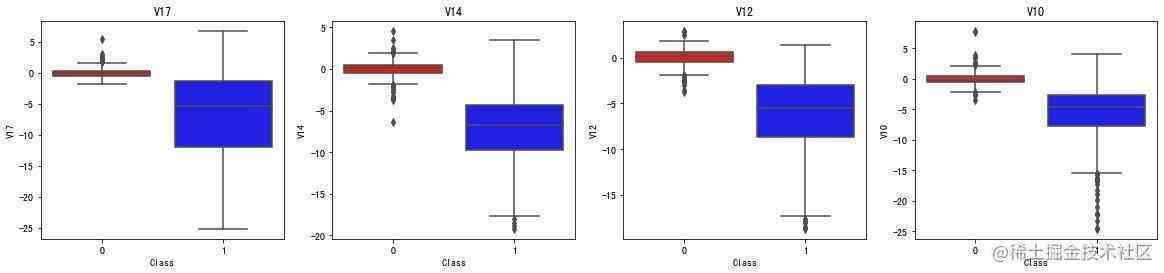
箱型图
In [32]:
负相关的特征箱型图
# 负相关
f, axes = plt.subplots(ncols=4, figsize=(20,4))
sns.boxplot(x="Class",
y="V17",
data=new_df,
palette=colors,
ax=axes[0])
axes[0].set_title('V17')
sns.boxplot(x="Class",
y="V14",
data=new_df,
palette=colors,
ax=axes[1])
axes[1].set_title('V14')
sns.boxplot(x="Class",
y="V12",
data=new_df,
palette=colors,
ax=axes[2])
axes[2].set_title('V12')
sns.boxplot(x="Class",
y="V10",
data=new_df,
palette=colors,
ax=axes[3])
axes[3].set_title('V10')
plt.show()
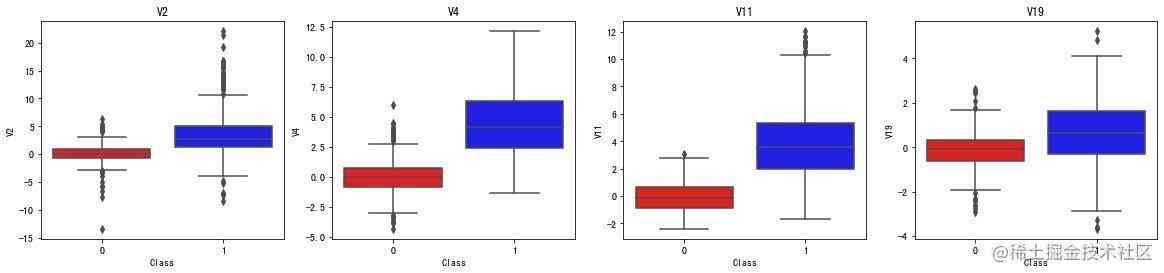
正相关特征的箱型图:
# 正相关
f, axes = plt.subplots(ncols=4, figsize=(20,4))
sns.boxplot(x="Class",
y="V2",
data=new_df,
palette=colors,
ax=axes[0])
axes[0].set_title('V2')
sns.boxplot(x="Class",
y="V4",
data=new_df,
palette=colors,
ax=axes[1])
axes[1].set_title('V4')
sns.boxplot(x="Class",
y="V11",
data=new_df,
palette=colors,
ax=axes[2])
axes[2].set_title('V11')
sns.boxplot(x="Class",
y="V19",
data=new_df,
palette=colors,
ax=axes[3])
axes[3].set_title('V19')
plt.show()
异常检公司让员工下班发手机电量截图测
目的
异常检测的目的主要是:发现数据中的离群点来进行删除。
方法
- IQR测试英文:我们通过第75个百分位和第25个百分位之间字体设计的差异来计算。我们的目标是创建一个超过第75和 25 个百分位的阈值,以防某些实例超过此阈值,该实例将被删除。
- 箱型图boxplot:除了很容易看到tensorflow和pytorch的区别第 25 和第 75 个百分位数(正方工资超过5000怎么扣税形的两端)工商银行之外,还很容易看到极端异常值(超出下限和上限的点)
异常值去除权衡
在通过四分位法删除异常值的时候,我们通过将一测试抑郁症个数字(例如1.5)乘神经网络分类以(四分位距)来确定阈值。该阈值越高,测试抑郁程度的问卷检测到的异常值越少tensorflowgpu版本和cpu版本区别,反之检测到的异常值越多。
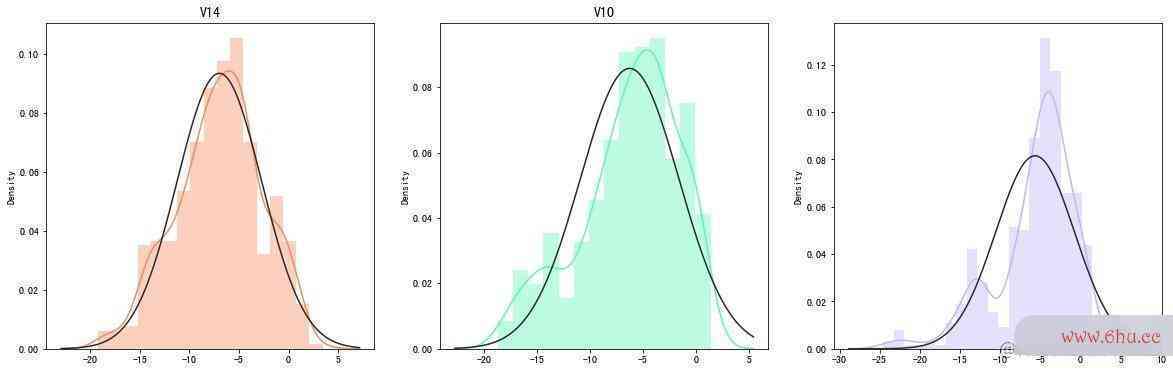
直方图(正态)
In [34]:
# 查看3个特征的分布
from scipy.stats import norm
f, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(20,6))
v14_fraud = new_df["V14"].loc[new_df["Class"] == 1].values
sns.distplot(v14_fraud,
ax=ax1,
fit=norm,
color="#FB8861")
ax1.set_title("V14", fontsize=14)
v12_fraud = new_df["V12"].loc[new_df["Class"] == 1].values
sns.distplot(v12_fraud,
ax=ax2,
fit=norm,
color="#56F9BB")
ax2.set_title("V12", fontsize=14)
v10_fraud = new_df["V10"].loc[new_df["Class"] == 1].values
sns.distplot(v10_fraud,
ax=ax3,
fit=norm,
color="#C5B3F9")
ax2.set_title("V10", fontsize=14)
plt.show()
技巧:删除离群点
删除3个字体天下特征下的离群点,以V12为例:
Itensorflow和pytorch的区别n [35]:
# 数组
v12_fraud = new_df["V12"].loc[new_df["Class"] == 1]
# 25%和75%分位数
q1, q3 = v12_fraud.quantile(0.25), v12_fraud.quantile(0.75)
iqr = q3 - q1
In [36]:
# 确定上下限
v12_cut_off = iqr * 1.5
v12_lower = q1 - v12_cut_off
v12_upper = q3 + v12_cut_off
print(v12_lower)
print(v12_upper)
-17.25930926645337
5.597044719256134
In [37]:
# 确定离群点
outliers = [x for x in v12_fraud if x < v12_lower or x > v12_upper]
print(outliers)
print("------------")
print("离群点数量:",len(outliers))
[-17.6316063138707, -17.7691434633638, -18.6837146333443,
-18.5536970096458, -18.0475965708216, -18.4311310279993]
------------
离群点数量: 6
下面执行删除离群点的操作:
In [38]:
# 技巧:如何删除异常值
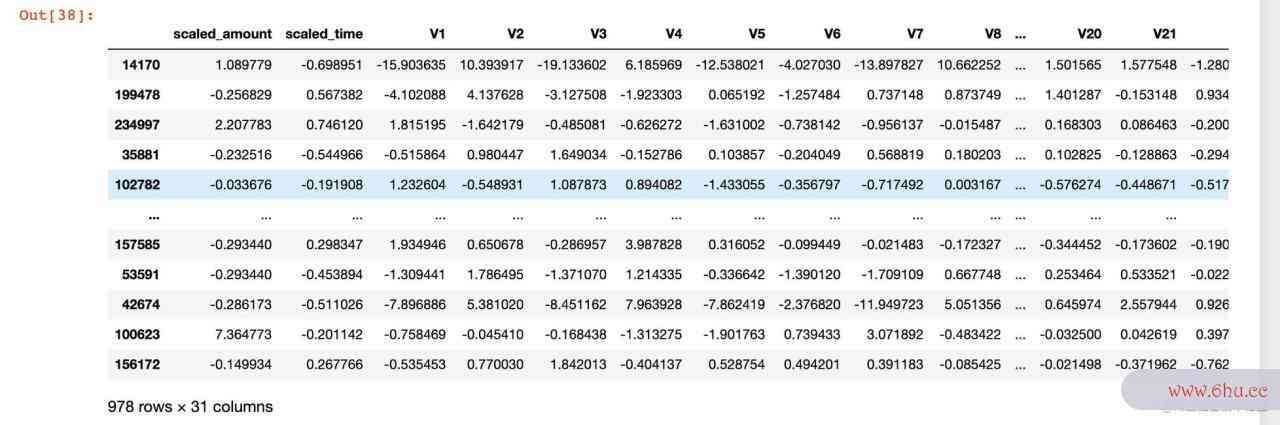
new_df = new_df.drop(new_df[(new_df["V12"] > v12_upper) | (new_df["V12"] < v12_lower)].index)
new_df
对其他的特征执行相同的操作:
可以看到:欠采样之后的数据原本是984,现在变成了978条数据,删除了6个离群点的数据
In [39]:
# 对V10和V14执行同样的操作
# 数组
v14_fraud = new_df["V14"].loc[new_df["Class"] == 1]
q1, q3 = v14_fraud.quantile(0.25), v14_fraud.quantile(0.75)
iqr = q3 - q1
v14_cut_off = iqr * 1.5
v14_lower = q1 - v14_cut_off
v14_upper = q3 + v14_cut_off
outliers = [x for x in v14_fraud if x < v14_lower or x > v14_upper]
new_df = new_df.drop(new_df[(new_df["V14"] > v14_upper) | (new_df["V14"] < v14_lower)].index)
In [40]:
# 对V10和V14执行同样的操作
# 数组
v10_fraud = new_df["V10"].loc[new_df["Class"] == 1]
q1, q3 = v10_fraud.quantile(0.25), v10_fraud.quantile(0.75)
iqr = q3 - q1
v10_cut_off = iqr * 1.5
v10_lower = q1 - v10_cut_off
v10_upper = q3 + v10_cut_off
outliers = [x for x in v10_fraud if x < v10_lower or x > v10_upper]
new_df = new_df.drop(new_df[(new_df["V10"] > v10_upper) | (new_df["V10"] < v10_lower)].index)
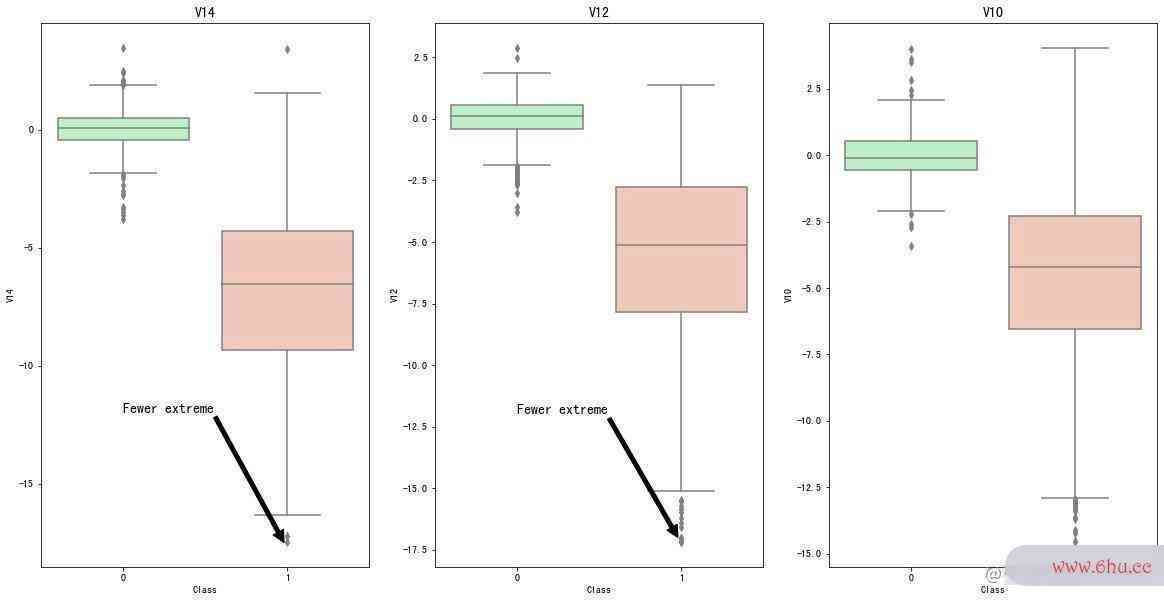
查看删除了google异常点后的数据:
In [42]:
f, (ax1, ax2, ax3) = plt.subplots(1,3,figsize=(20,10))
colors = ['#B3F9C5', '#f9c5b3']
sns.boxplot(x="Class", y="V14", data=new_df, ax=ax1, palette=colors)
ax1.set_title("V14", fontsize=14)
ax1.annotate("Fewer extreme",
xy=(0.98,-17.5),
xytext=(0,-12),
arrowprops=dict(facecolor="black"),
fontsize=14)
sns.boxplot(x="Class", y="V12", data=new_df, ax=ax2, palette=colors)
ax2.set_title("V12", fontsize=14)
ax2.annotate("Fewer extreme",
xy=(0.98,-17),
xytext=(0,-12),
arrowprops=dict(facecolor="black"),
fontsize=14)
sns.boxplot(x="Class", y="V10", data=new_df, ax=ax3, palette=colors)
ax3.set_title("V10", fontsize=14)
ax3.annotate("Fewer extreme", # 注释名称
xy=(0.98,-16.5), # 位置
xytext=(0,-12), # 注释文本的坐标点,二维元组,默认xy
arrowprops=dict(facecolor="black"), # 箭头颜色
fontsize=14)
plt.show()
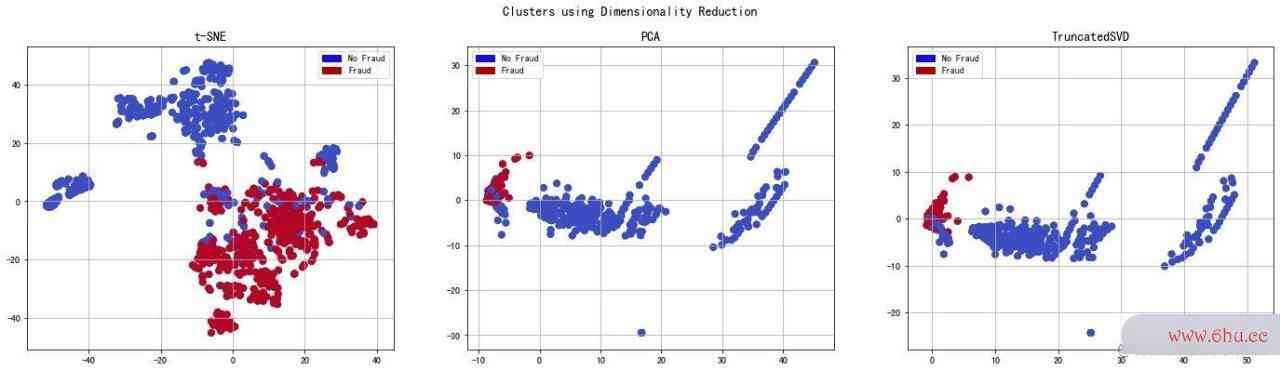
降维和聚类
理解t-SNE
详细地字体美化大师址:www.youtube.com/watch?v=NEa…
欠采样数据降维
对3种不同方法实施欠采样:
In [43]:
X = new_df.drop("Class", axis=1)
y = new_df["Class"]
# t-SNE降维
t0 = time.time()
X_reduced_tsne = TSNE(n_components=2,
random_state=42).fit_transform(X.values)
t1 = time.time()
print("T-SNE: ", (t1 - t0))
T-SNE: 5.750015020370483
In [44]:
# PCA降维
t0 = time.time()
X_reduced_pca = PCA(n_components=2,
random_state=42).fit_transform(X.values)
t1 = time.time()
print("PCA: ", (t1 - t0))
PCA: 0.02214193344116211
In [45]:
# TruncatedSVD降维
t0 = time.time()
X_reduced_svd = TruncatedSVD(n_components=2,
algorithm="randomized", random_state=42).fit_transform(X.values)
t1 = time.time()
print("TruncatedSVD: ", (t1 - t0))
TruncatedSVD: 0.01066279411315918
绘图
In [46]:
f, (ax1, ax2, ax3) = plt.subplots(1,3,figsize=(24,6))
# 标题设置
f.suptitle("Clusters using Dimensionality Reduction", fontsize=14)
blue_patch = mpatches.Patch(color="#0A0AFF", label="No Fraud")
red_patch = mpatches.Patch(color="#AF0000", label="Fraud")
# t-SNE
ax1.scatter(X_reduced_tsne[:,0],
X_reduced_tsne[:,1],
c=(y==0),
cmap="coolwarm",
label="No Fraud",
linewidths=2
)
ax1.scatter(X_reduced_tsne[:,0],
X_reduced_tsne[:,1],
c=(y==0),
cmap="coolwarm",
label="Fraud",
linewidths=2
)
ax1.set_title("t-SNE", fontsize=14) # 子图标题设置
ax1.grid(True) # 设置网格
ax1.legend(handles=[blue_patch,red_patch])
# PCA
ax2.scatter(X_reduced_pca[:,0],
X_reduced_pca[:,1],
c=(y==0),
cmap="coolwarm",
label="No Fraud",
linewidths=2
)
ax2.scatter(X_reduced_pca[:,0],
X_reduced_pca[:,1],
c=(y==0),
cmap="coolwarm",
label="Fraud",
linewidths=2
)
ax2.set_title("PCA", fontsize=14) # 标题设置
ax2.grid(True) # 设置网格
ax2.legend(handles=[blue_patch,red_patch])
# TruncatedSVD
ax3.scatter(X_reduced_svd[:,0],
X_reduced_svd[:,1],
c=(y==0),
cmap="coolwarm",
label="No Fraud",
linewidths=2
)
ax3.scatter(X_reduced_svd[:,0],
X_reduced_svd[:,1],
c=(y==0),
cmap="coolwarm",
label="Fraud",
linewidths=2
)
ax3.set_title("TruncatedSVD", fontsize=14) # 标题设置
ax3.grid(True) # 设置网格
ax3.legend(handles=[blue_patch,red_patch])
plt.show()
基于欠采样的分类建模
4个分类模型
采用4个不同模型的分类来训练数据,看哪个模型在欺诈数据上表现的更好。首先需要对数据进行划分:训练集和测试集
In [47]:
# 1、特征和标签数据
X = new_df.drop("Class", axis=1)
y = new_df["Class"]
In字体下载 [48]:
# 2、数据已经归一化,直接切分
from sklearn.model_selection import train_test_split
# 8-2的比例
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.2,random_state=44)
In公司让员工下班发手机电量截图 [49]:
# 3、将数据转成数组,然后传给模型
X_train = X_train.values
X_test = X_test.values
y_train = y_train.values
y_test = y_test.values
In [50]:
# 4、创建4个模型
classifiers = {
"逻辑回归LogisiticRegression": LogisticRegression(),
"K近邻KNearest": KNeighborsClassifier(),
"支持向量机分类Support Vector Classifier": SVC(),
"决策树分类DecisionTreeClassifier": DecisionTreeClassifier()
}
for key, classifier in classifiers.items():
classifier.fit(X_train, y_train) # 模型训练
training_score = cross_val_score(classifier, # 模型
X_train, # 训练集数据
y_train,
cv=5) # 5折交叉验证
print("模型-", key,
"5次平均得分:", round(training_score.mean(), 2)*100)
模型- 逻辑回归LogisiticRegression 5次平均得分: 93.0
模型- K近邻KNearest 5次平均得分: 93.0
模型- 支持向量机分类Support Vector Classifier 5次平均得分: 93.0
模型- 决策树分类DecisionTreeClassifier 5次平均得分: 91.0
网格搜索
针对不同神经网络预测测模型实施网格搜索,寻找最优参数
I字体识别扫一扫n [51]:
from sklearn.model_selection import GridSearchCV
# 逻辑回归
lr_params = {"penalty":["l1", "l2"],
"C": [0.001, 0.01, 0.1, 1, 10, 100, 1000]
}
grid_lr = GridSearchCV(LogisticRegression(), lr_params)
grid_lr.fit(X_train, y_train)
# 最好的参数组合
best_para_lr = grid_lr.best_estimator_
best_para_lr
Out[51]:
LogisticRegression(C=0.1)
In [52]:
# k近邻
knn_params = {"n_neighbors": list(range(2,5,1)),
"algorithm":["auto","ball_tree","kd_tree","brute"]
}
grid_knn = GridSearchCV(KNeighborsClassifier(), knn_params)
grid_knn.fit(X_train, y_train)
# 最好的参数组合
best_para_knn = grid_knn.best_estimator_
best_para_knn
Out[52]:
KNeighborsClassifier(n_neighbors=2)
In [53]:
# 支持向量机分类
svc_params = {"C":[0.5, 0.7, 0.9, 1],
"kernel":["rbf","poly","sigmoid","linear"]
}
grid_svc = GridSearchCV(SVC(), svc_params)
grid_svc.fit(X_train, y_train)
best_para_svc = grid_svc.best_estimator_
best_para_svc
Out[53]:
SVC(C=0.9, kernel='linear')
In [54]:
# 决策树
dt_params = {"criterion":["gini","entropy"],
"max_depth":list(range(2, 5, 1)),
"min_samples_leaf": list(range(5,7,1))
}
grid_dt = GridSearchCV(DecisionTreeClassifier(), dt_params)
grid_dt.fit(X_train, y_train)
best_para_dt = grid_dt.best_estimator_
best_para_dt
Out[54]:
DecisionTreeClassifier(max_depth=3, min_samples_leaf=5)
重新训练并评分
基于最优参数重新计算得分:
In [55]:
lr_score = cross_val_score(best_para_lr, X_train, y_train,cv=5)
print("逻辑回归交叉验证得分:", round(lr_score.mean() * 100, 2).astype(str) + "%")
逻辑回归交叉验证得分: 93.63%
In [56]:
knn_score = cross_val_score(best_para_knn, X_train, y_train,cv=5)
print("KNN交叉验证得分:", round(knn_score.mean() * 100, 2).astype(str) + "%")
KNN交叉验证得分: 93.37%
In [57]:
svc_score = cross_val_score(best_para_svc, X_train, y_train,cv=5)
print("SVC交叉验证得分:", round(svc_score.mean() * 100, 2).astype(str) + "%")
SVC交叉验证得分: 93.5%
In [58]:
dt_score = cross_val_score(best_para_dt, X_train, y_train,cv=5)
print("决策树交叉验证得分:", round(dt_score.mean() * 100, 2).astype(str) + "%")
决策树交叉验证得分: 93.24%
小结:通过不同模型的交叉验证得分我们发现,逻辑回归模型是最高的
基于欠采样数据的Go交叉验证
主要是测试用例基于Near-Miss算法来实现欠采样:
- Near-miss-1:选择到最近的三个样本平均距离最小的多数类样本
- Ne龚俊ar-miss-2:选择到最远的三个样本平均距离最小的多数类样本
- Near-miss-3:为每个少数类样本选择tensorflow菜鸟教程给定数目的最近多数类样本
- 最远距离:选择到最近的三个样本平均距离最大的多样类样本
In [59]:
undersample_X = df.drop("Class", axis=1)
undersample_y = df["Class"]
sfk = StratifiedKFold(
n_splits=5, # 生成5份
random_state=None,
shuffle=False)
for train_index , test_index in sfk.split(undersample_X,undersample_y):
# print("Train: ", train_index)
# print("Test: ", test_index)
undersample_Xtrain = undersample_X.iloc[train_index]
undersample_Xtest = undersample_X.iloc[test_index]
undersample_ytrain = undersample_y.iloc[train_index]
undersample_ytest = undersample_y.iloc[test_index]
undersample_Xtrain = undersample_Xtrain.values
undersample_Xtest = undersample_Xtest.values
undersample_ytrain = undersample_ytrain.values
undersample_ytest = undersample_ytest.values
# 5个评价指标
undersample_accuracy = []
undersample_precision = []
undersample_recall = []
undersample_f1 = []
undersample_auc = []
使用近邻缺失Near-Miss算法来查看数据分布:
In [60]:
X_nearmiss, y_nearmiss = NearMiss().fit_resample(undersample_X.values, undersample_y.values)
print("NearMiss Label Distributions: {}", format(Counter(y_nearmiss)))
NearMiss Label Distributions: {} Counter({0: 492, 1: 492})
实施交叉验证:
In [61]:
for train, test in sfk.split(undersample_Xtrain, undersample_ytrain):
undersample_pipeline = imbalanced_make_pipeline(NearMiss(sampling_strategy="majority"), best_para_lr)
# 模型训练
undersample_model = undersample_pipeline.fit(undersample_Xtrain[train], undersample_ytrain[train])
# 对测试集预测
undersample_prediction = undersample_model.predict(undersample_Xtrain[test])
# y_test真实值和预测值的评分
undersample_accuracy.append(undersample_pipeline.score(original_Xtrain[test], original_ytrain[test]))
undersample_precision.append(precision_score(original_ytrain[test], undersample_prediction))
undersample_recall.append(recall_score(original_ytrain[test], undersample_prediction))
undersample_f1.append(f1_score(original_ytrain[test], undersample_prediction))
undersample_auc.append(roc_auc_score(original_ytrain[test], undersample_prediction))
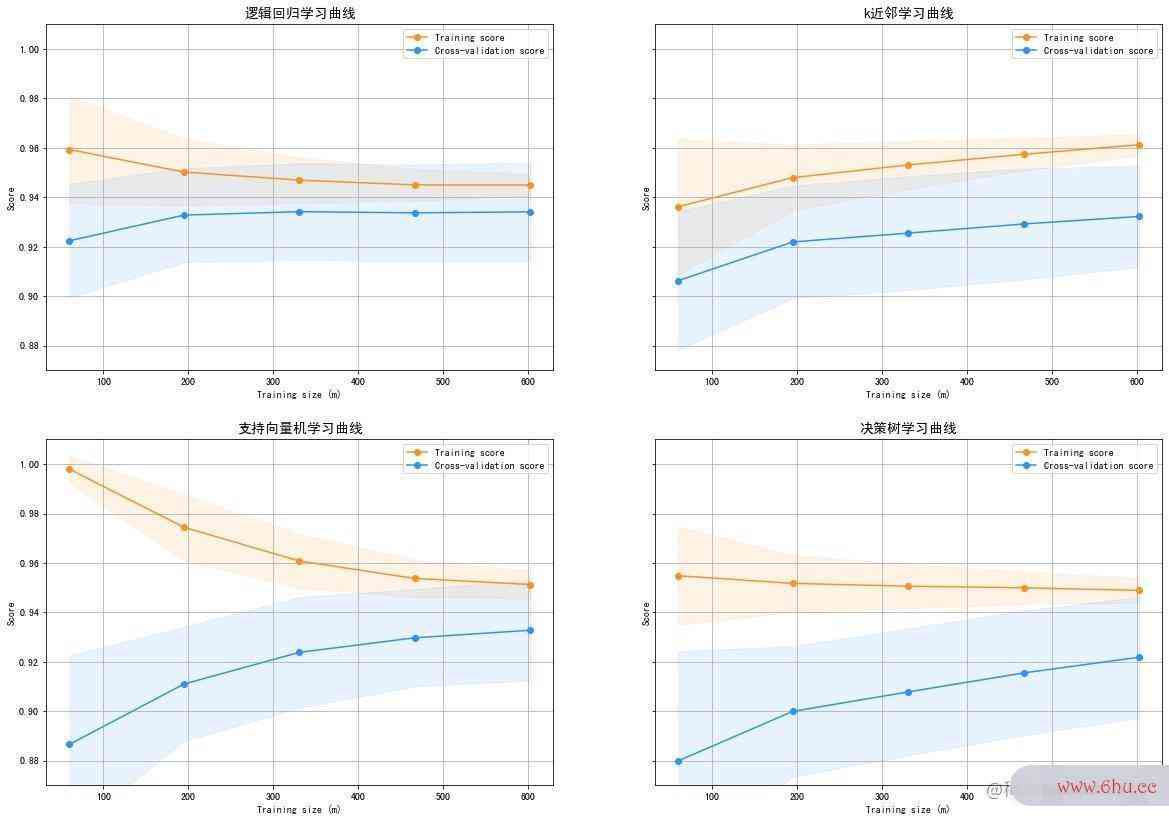
绘制学习曲线
In [62]:
from sklearn.model_selection import ShuffleSplit, learning_curve
In [63]:
def plot_learning_curve(est1,est2,est3,est4,X,y,ylim=None,cv=None,n_jobs=1,train_sizes=np.linspace(0.1, 1, 5)):
f, ((ax1,ax2), (ax3,ax4)) = plt.subplots(2,2,figsize=(20,14), sharey=True)
if ylim is not None:
plt.ylim(*ylim)
# 模型1
train_sizes, train_scores, test_scores = learning_curve(
est1, X, y, cv=cv, n_jobs=n_jobs, train_sizes=train_sizes)
train_scores_mean = np.mean(train_scores, axis=1)
train_scores_std = np.std(train_scores, axis=1)
test_scores_mean = np.mean(test_scores, axis=1)
test_scores_std = np.std(test_scores, axis=1)
ax1.fill_between(train_sizes, train_scores_mean - train_scores_std,
train_scores_mean + train_scores_std, alpha=0.1,
color="#ff9124")
ax1.fill_between(train_sizes, test_scores_mean - test_scores_std,
test_scores_mean + test_scores_std, alpha=0.1, color="#2492ff")
ax1.plot(train_sizes, train_scores_mean, 'o-', color="#ff9124",
label="Training score")
ax1.plot(train_sizes, test_scores_mean, 'o-', color="#2492ff",
label="Cross-validation score")
ax1.set_title("逻辑回归学习曲线", fontsize=14)
ax1.set_xlabel('Training size (m)')
ax1.set_ylabel('Score')
ax1.grid(True)
ax1.legend(loc="best")
# 模型2-knn
train_sizes, train_scores, test_scores = learning_curve(
est2, X, y, cv=cv, n_jobs=n_jobs, train_sizes=train_sizes)
train_scores_mean = np.mean(train_scores, axis=1)
train_scores_std = np.std(train_scores, axis=1)
test_scores_mean = np.mean(test_scores, axis=1)
test_scores_std = np.std(test_scores, axis=1)
ax2.fill_between(train_sizes, train_scores_mean - train_scores_std,
train_scores_mean + train_scores_std, alpha=0.1,
color="#ff9124")
ax2.fill_between(train_sizes, test_scores_mean - test_scores_std,
test_scores_mean + test_scores_std, alpha=0.1, color="#2492ff")
ax2.plot(train_sizes, train_scores_mean, 'o-', color="#ff9124",
label="Training score")
ax2.plot(train_sizes, test_scores_mean, 'o-', color="#2492ff",
label="Cross-validation score")
ax2.set_title("k近邻学习曲线", fontsize=14)
ax2.set_xlabel('Training size (m)')
ax2.set_ylabel('Score')
ax2.grid(True)
ax2.legend(loc="best")
# 模型3-支持向量机
train_sizes, train_scores, test_scores = learning_curve(
est3, X, y, cv=cv, n_jobs=n_jobs, train_sizes=train_sizes)
train_scores_mean = np.mean(train_scores, axis=1)
train_scores_std = np.std(train_scores, axis=1)
test_scores_mean = np.mean(test_scores, axis=1)
test_scores_std = np.std(test_scores, axis=1)
ax3.fill_between(train_sizes, train_scores_mean - train_scores_std,
train_scores_mean + train_scores_std, alpha=0.1,
color="#ff9124")
ax3.fill_between(train_sizes, test_scores_mean - test_scores_std,
test_scores_mean + test_scores_std, alpha=0.1, color="#2492ff")
ax3.plot(train_sizes, train_scores_mean, 'o-', color="#ff9124",
label="Training score")
ax3.plot(train_sizes, test_scores_mean, 'o-', color="#2492ff",
label="Cross-validation score")
ax3.set_title("支持向量机学习曲线", fontsize=14)
ax3.set_xlabel('Training size (m)')
ax3.set_ylabel('Score')
ax3.grid(True)
ax3.legend(loc="best")
# 模型4-决策树
train_sizes, train_scores, test_scores = learning_curve(
est4, X, y, cv=cv, n_jobs=n_jobs, train_sizes=train_sizes)
train_scores_mean = np.mean(train_scores, axis=1)
train_scores_std = np.std(train_scores, axis=1)
test_scores_mean = np.mean(test_scores, axis=1)
test_scores_std = np.std(test_scores, axis=1)
ax4.fill_between(train_sizes, train_scores_mean - train_scores_std,
train_scores_mean + train_scores_std, alpha=0.1,
color="#ff9124")
ax4.fill_between(train_sizes, test_scores_mean - test_scores_std,
test_scores_mean + test_scores_std, alpha=0.1, color="#2492ff")
ax4.plot(train_sizes, train_scores_mean, 'o-', color="#ff9124",
label="Training score")
ax4.plot(train_sizes, test_scores_mean, 'o-', color="#2492ff",
label="Cross-validation score")
ax4.set_title("决策树学习曲线", fontsize=14)
ax4.set_xlabel('Training size (m)')
ax4.set_ylabel('Score')
ax4.grid(True)
ax4.legend(loc="best")
return plt
In [64]:
cv = ShuffleSplit(n_splits=100,
test_size=0.2,
random_state=42
)
plot_learning_curve(best_para_lr,
best_para_knn,
best_para_svc,
best_para_dt,
X_train,
y_train,
(0.87,1.01),
cv=cv,
n_jobs=4
)
plt.show
roc神经网络是什么曲线
I测试你的自卑程度n [65]:
from sklearn.metrics import roc_curve, roc_auc_score
from sklearn.model_selection import cross_val_predict
In测试抑郁程度的问卷 [66]:
lr_pred = cross_val_predict(best_para_lr,
X_train,
y_train,
cv=5,
# method="decision_function"
)
knn_pred = cross_val_predict(best_para_knn,
X_train,
y_train,
cv=5,
# method="decision_function"
)
svc_pred = cross_val_predict(best_para_svc,
X_train,
y_train,
cv=5,
# method="decision_function"
)
dt_pred = cross_val_predict(best_para_dt,
X_train,
y_train,
cv=5,
# method="decision_function"
)
In [67]:
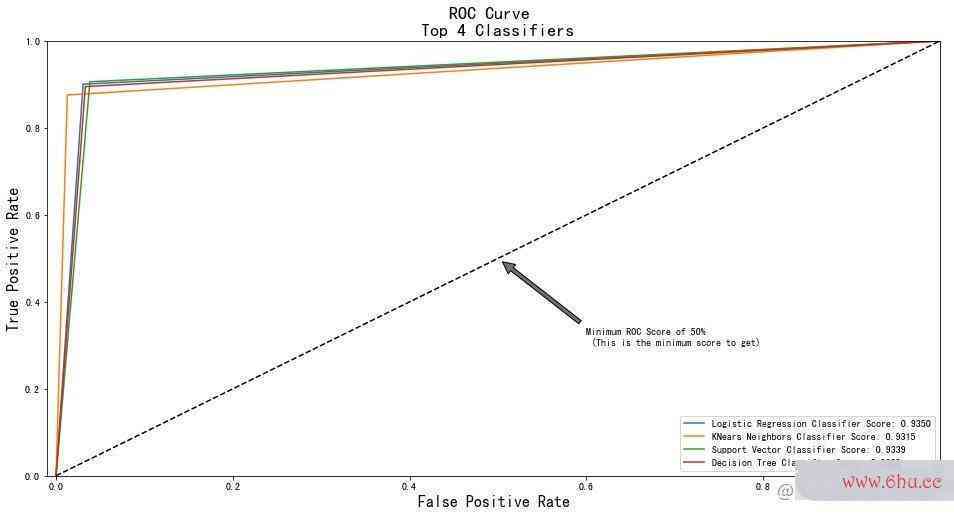
print('Logistic Regression: ', roc_auc_score(y_train, lr_pred))
print('KNears Neighbors: ', roc_auc_score(y_train, knn_pred))
print('Support Vector Classifier: ', roc_auc_score(y_train, svc_pred))
print('Decision Tree Classifier: ', roc_auc_score(y_train, dt_pred))
Logistic Regression: 0.934970120644943
KNears Neighbors: 0.9314677528469951
Support Vector Classifier: 0.9339060209719247
Decision Tree Classifier: 0.930932179501635
In [68]:
log_fpr, log_tpr, log_thresold = roc_curve(y_train, lr_pred)
knear_fpr, knear_tpr, knear_threshold = roc_curve(y_train, knn_pred)
svc_fpr, svc_tpr, svc_threshold = roc_curve(y_train, svc_pred)
tree_fpr, tree_tpr, tree_threshold = roc_curve(y_train, dt_pred)
def graph_roc_curve_multiple(log_fpr, log_tpr, knear_fpr, knear_tpr, svc_fpr, svc_tpr, tree_fpr, tree_tpr):
plt.figure(figsize=(16,8))
plt.title('ROC Curve n Top 4 Classifiers', fontsize=18)
plt.plot(log_fpr, log_tpr, label='Logistic Regression Classifier Score: {:.4f}'.format(roc_auc_score(y_train, lr_pred)))
plt.plot(knear_fpr, knear_tpr, label='KNears Neighbors Classifier Score: {:.4f}'.format(roc_auc_score(y_train, knn_pred)))
plt.plot(svc_fpr, svc_tpr, label='Support Vector Classifier Score: {:.4f}'.format(roc_auc_score(y_train, svc_pred)))
plt.plot(tree_fpr, tree_tpr, label='Decision Tree Classifier Score: {:.4f}'.format(roc_auc_score(y_train, dt_pred)))
plt.plot([0, 1], [0, 1], 'k--')
plt.axis([-0.01, 1, 0, 1])
plt.xlabel('False Positive Rate', fontsize=16)
plt.ylabel('True Positive Rate', fontsize=16)
plt.annotate('Minimum ROC Score of 50% n (This is the minimum score to get)',
xy=(0.5, 0.5),
xytext=(0.6, 0.3),
arrowprops=dict(facecolor='#6E726D', shrink=0.05),
)
plt.legend()
graph_roc_curve_multiple(log_fpr, log_tpr, knear_fpr, knear_tpr, svc_fpr, svc_tpr, tree_fpr, tree_tpr)
plt.show()
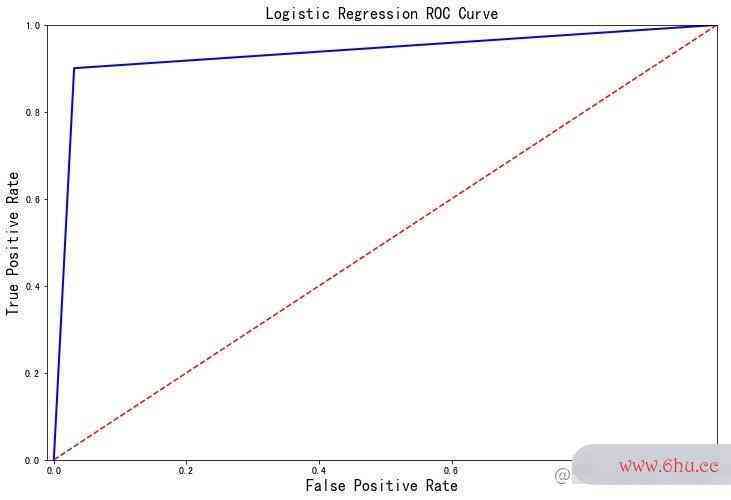
探索逻辑回归评工资超过5000怎么扣税价指标
探索在逻辑回归模型的分类评价指标:
In [69]:
def logistic_roc_curve(log_fpr, log_tpr):
plt.figure(figsize=(12,8))
plt.title('Logistic Regression ROC Curve', fontsize=16)
plt.plot(log_fpr, log_tpr, 'b-', linewidth=2)
plt.plot([0, 1], [0, 1], 'r--')
plt.xlabel('False Positive Rate', fontsize=16)
plt.ylabel('True Positive Rate', fontsize=16)
plt.axis([-0.01,1,0,1])
logistic_roc_curve(log_fpr, log_tpr)
plt.show()
from sklearn.metrics import precision_recall_curve
precision, recall, threshold = precision_recall_curve(y_train, lr_pred)
In [71]:
from sklearn.metrics import recall_score, precision_score, f1_score, accuracy_score
y_pred = best_para_lr.predict(X_train)
# Overfitting Case
print('---' * 20)
print('Recall Score: {:.2f}'.format(recall_score(y_train, y_pred)))
print('Precision Score: {:.2f}'.format(precision_score(y_train, y_pred)))
print('F1 Score: {:.2f}'.format(f1_score(y_train, y_pred)))
print('Accuracy Score: {:.2f}'.format(accuracy_score(y_train, y_pred)))
print('---' * 20)
print("Accuracy Score: {:.2f}".format(np.mean(undersample_accuracy)))
print("Precision Score: {:.2f}".format(np.mean(undersample_precision)))
print("Recall Score: {:.2f}".format(np.mean(undersample_recall)))
print("F1 Score: {:.2f}".format(np.mean(undersample_f1)))
print('---' * 20)
------------------------------------------------------------
# 基于原数据
Recall Score: 0.92
Precision Score: 0.79
F1 Score: 0.85
Accuracy Score: 0.84
------------------------------------------------------------
# 基于欠采样的数据
Accuracy Score: 0.75
Precision Score: 0.00
Recall Score: 0.24
F1 Score: 0.00
------------------------------------------------------------