AB试验是辅佐公司科学决策的有力东西，它能够科学谨慎地评价功用/UI/策略/营销等改动的作用，为后续迭代、扩量提供指导。

每分每秒都有大量AB试验正在运行，这些试验不断影响着公司或大或小的决策，正因如此，正确了解、正确运用AB试验显得十分必要。

本文旨在介绍AB试验背后首要的核算学原理和办法——假定查验、最小样本量的根本概念，以及在实操过程中怎么运用这两种技术：如安在试验后运用假定查验做出科学谨慎的试验定论，如安在试验前测算最小样本量确保试验具有满意的核算成效。期望经过本文能对正确了解和运用AB试验有所助益。

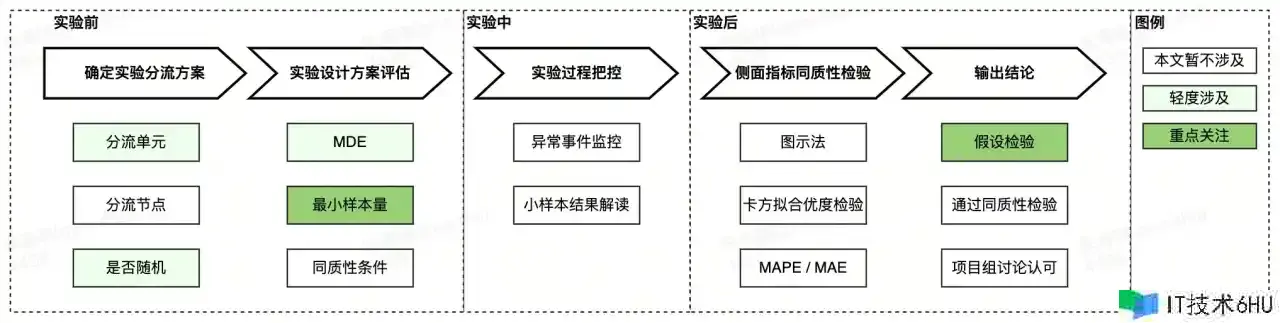
一、评论规模

下图罗列了部分常用的假定查验品种及其运用场景：

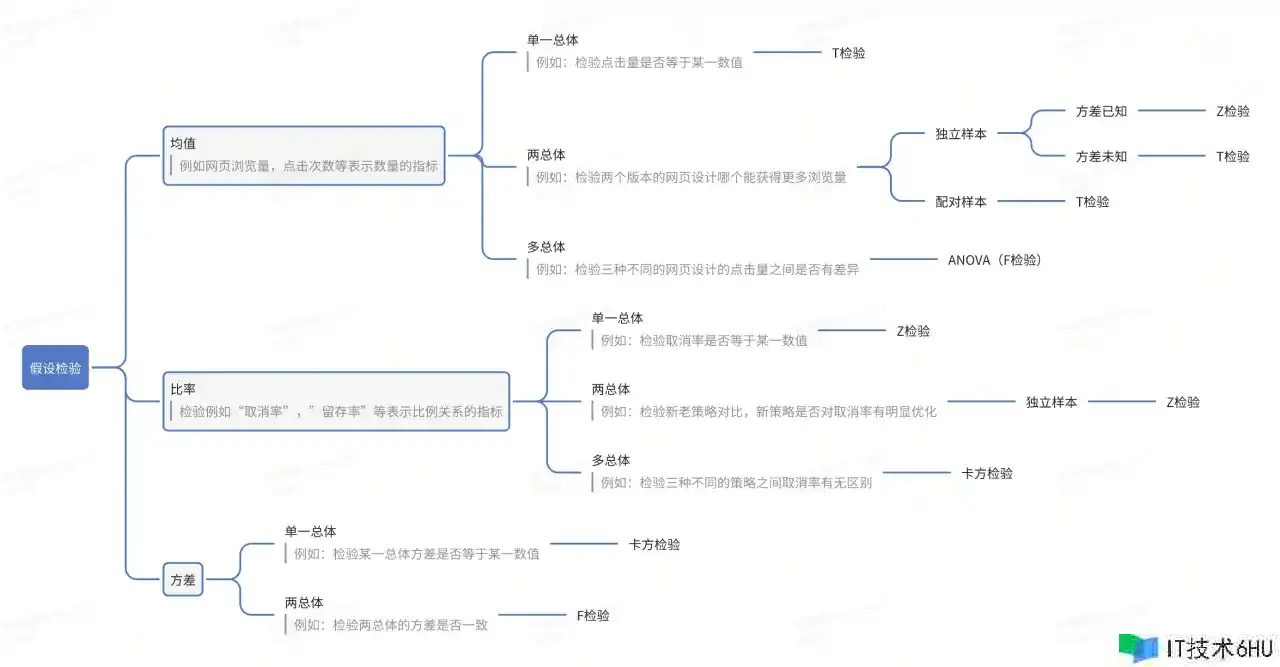
本文仅评论AB试验中id随机分流场景下，最常见的两种假定查验办法和其相应的最小样本量测算：

查验办法	适用场景	举例
独立样本t查验	id分流，查验某一个试验组和对照组间均值是否有差异	用户id分流，查验人均完单量
独立样本z查验	id分流，查验某一个试验组和对照组间比率是否有差异	订单id分流，查验订单配对率

以下几种场景不适用本文介绍的办法：

粗粒度的分流办法：如货拉拉场景下的时刻片轮播、城市群交替轮播等（需运用Bootstrap）。
多个分组的联合查验：如组1、组2、组3均值/比率是否共同（需运用ANOVA / 卡方查验）。
分流单元和剖析单元不共同：如用户id分流的AB试验需求查验订单配对率（需运用Delta Method / Bootstrap）。
试验不满意SUTVA准则（试验组个别和对照组个别不彼此独立，存在彼此干扰）。

以上部分场景在本系列的其他文章将会介绍。

二、假定查验

2.1. 根本流程

在获得 AB试验 数据以后，需求运用假定查验来判别试验组和对照组的差异仅仅是数据动摇，还是具有核算意义的收益——只要当差异满意大（大于动摇阈值）时，咱们才以为试验具有实在收益，因为此时差异大到不太可能单纯由动摇导致。

下图展示假定查验的根本流程，其间触及的概念会在下文介绍：

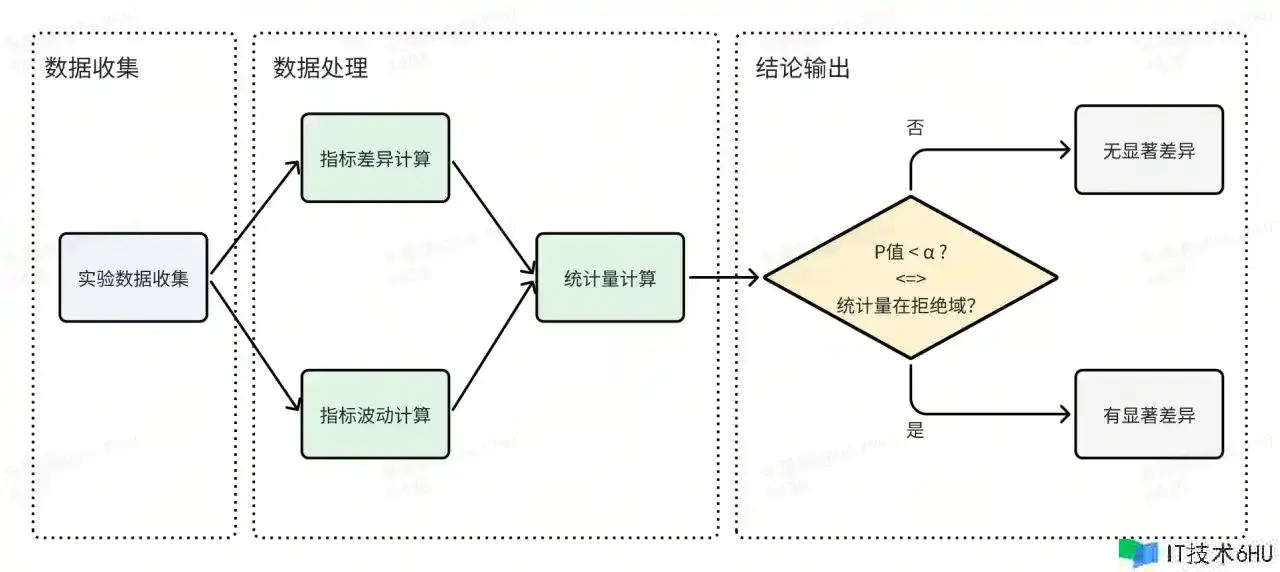
2.2. 根本概念

1. 假定查验

假定查验(中的参数查验)是先对整体的参数提出某种假定，然后运用样本数据判别假定是否树立的过程。逻辑上运用反证法，核算上依据小概率思维。

（小概率思维是指小概率事情（p值 < 0.05）在一次试验中根本上不会产生。反证法是指先提出假定，再用适当的核算办法确认假定树立的可能性大小；如可能性小，则以为假定不树立。）

原假定：是试验者想搜集依据予以反对的假定 ,又称“零假定”，记为 H0；

备择假定：也称“研讨假定”，是试验者想搜集依据予以支撑的假定，记为 H1；

原假定和备择假定是一个完备事情组：在一项假定查验中，原假定和备择假定必有一个树立，而且只要一个树立。

AB试验 中H0和H1举例：AB试验的意图是经过反证法证明测验版别和对照版别有显着的不同（提升），所以咱们的原假定是测验版别的整体均值等于对照版别的整体均值，备择假定则是两者均值不相等。

H0	H1
测验版别的整体均值 = 对照版别的整体均值	测验版别的整体均值 ≠ 对照版别的整体均值

2. 核算量

咱们常用「试验组目标 – 对照组目标」来衡量AB试验作用：

$= 试验组目标 - 对照组目标$

实践上是一个环绕试验收益动摇的随机变量（假如无法了解这一点，能够幻想进行1000次AA试验，则1000次试验的收益将是一个环绕着0动摇的变量）。咱们对其做标准化处理，得到AB试验常用的核算量：

$核算量=()核算量=frac{hat{}}{(hat{})}$

其形式为：（试验组目标 – 对照组目标）/（两组目标差异的标准差），在样本量足够时，核算量近似遵守标准差为1的正态分布。

3. 第一类过错 & 第二类过错

第一类过错又称弃真过错，表明原假定为真时回绝原假定的过错。

第二类过错又称取伪过错，表明原假定为假时未回绝原假定的过错。

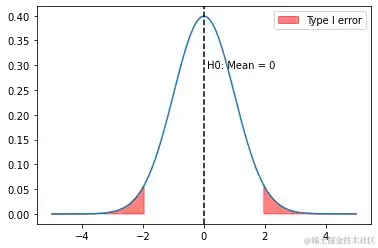
图一

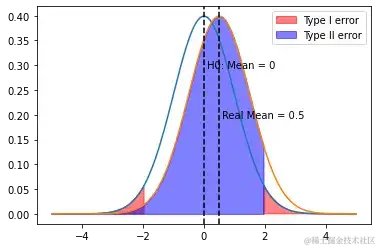
图二

图一：若H0为真，则核算量落入回绝域（红）的概率为

图二：两组实践存在差异，但核算量未落入回绝域（红）概率为

第一类过错产生的概率记为 (Alpha)。又称显着性水平。其事务意义是试验组和对照组实践无差异，但咱们依据数据成果误判为有差异的概率。

是一个需求咱们提前设定的概率值。因为比较第二类过错，第一类过错更加严重，因而取值应尽可能小。最常用的值是 0.05(5%)。

咱们常说的在显着性水平5%水平下显着，就是指依据试验数据咱们得出两组存在差异的定论，该定论犯第一类过错的概率≤5%。

第二类过错产生的概率记为 (Beta)。1-又称核算成效。核算成效会在第三部分介绍最小样本量时具体介绍。

5. 回绝域

回绝原假定时核算量的取值规模，核算量落入回绝域的概率 = 显着性水平。

决议了回绝域，反之也能够说回绝域决议了，两者能够彼此推导。

6. p值 (p)

P值（P value）是当原假定为真时，观察到与样本成果相当或更极点的成果呈现的概率。

假如P值低于咱们提前设置的显着性水平，依据小概率原理，咱们就有理由回绝原假定。P值越小，咱们回绝原假定的理由越充沛。

2.3. 两整体均值的假定查验

1. 典型场景

订单id随机分流，查验订单平均价格。
用户id随机分流，查验用户平均完单量。

2. 树立假定

查验两个整体均值，共有三种形式：

$H_0:_1-_2=d$ $Ha:1−2≠dH_a:_1-_2neq d$ 【双侧查验】

$H0:1−2≤dH_0:_1-_2le d$ $H_a:_1-_2>d$ 【右单侧查验】

$H0:1−2≥dH_0:_1-_2ge d$ $H_a:_1-_2$ 【左单侧查验】

$_1$ 表明试验组均值， $_2$ 表明对照组均值。在AB试验中最常见的情况是d = 0。

3. 核算核算量

当d = 0即 $_1$ = $_2$ 时，核算量t的公式为：

${_1} -hat {_2}}{sqrt{s^2(cfrac{1}{n_1} cfrac{1}{n_2})}} sim N(0,1)$

其间： $n2−2s^2= cfrac{sum_{i=1}^{n_1}{(Y_1(i)-hat{_1})^2} sum_{i=1}^{n_2}{(Y_2(i)-hat{_2})^2}}{n_1 n_2-2}$

其间， $1hat{_1}$ 、 $2hat{_2}$ 分别为试验组均值和对照组均值的点估量量（即试验数据核算出的均值），

$Y_1(i)$ 、 $Y_2(i)$ 分别为组1、组2的个别。

t核算量的分子是试验组与对照组均值差异的点估量，分母是测算得出的两组均值差异的标准差。

通常而言AB试验样本量满意足够，核算量t近似遵守正态分布。

4. 查验假定

在 = 0.05的条件下： $Z1−a2=1.96Z_{1-frac{a}{2}} = 1.96$ ， $Z_a = -1.6$ ， $Z_{1-a} = 1.6$

：正态分布CDF

当P值低于（等价于核算量t落入回绝域），则回绝原假定：组1和组2存在显着差异。

不然不回绝原假定：组1和组2不存在显着差异。

双侧查验	右单侧查验	左单侧查验
假定	H₀:₁ = ₂ H₁:₁ ≠ ₂	H₀:₁ ≤ ₂ H₁:₁ > ₂	H₀:₁ ≥ ₂ H₁:₁ < ₂
回绝域	\|t\| ≥ Z_1-/2	t ≥ Z_1-	t ≤ Z
P值	2-2(\|t\|)	1-(t)	(t)
P值决策	P_值 < , 回绝H₀

2.4. 两整体比率的假定查验

1. 典型场景

订单id随机分流，查验订单撤销率、配对率。
用户id随机分流，查验用户转化率。

2. 树立假定

查验两个整体比率，共有三种形式：

$H_0:p_1-p_2=d$ $Ha:p1−p2≠dH_a:p_1-p_2neq d$ 【双侧查验】

$H0:p1−p2≤dH_0:p_1-p_2le d$ $H_a:p_1-p_2>d$ 【右单侧查验】

$H0:p1−p2≥dH_0:p_1-p_2ge d$ $H_a:p_1-p_2<d$ 【左单侧查验】

$p_1$ 表明试验组的比率， $p_2$ 表明对照组的比率。在AB试验中最常见的情况是d = 0。

3. 核算核算量

在d = 0即 $u_1$ = $u_2$ 时，核算量t的公式为：

$frac{(hat{p_1} – hat{p_2})}{sqrt{hat{p}(1-hat{p})(frac{1}{n_1} frac{1}{n_2})}}sim N(0,1)$

其间， $p1hat{p_1}$ , $p2hat{p_2}$ 分别为试验组比率和对照组比率的点估量量（即试验数据核算出的比率）， $frac{n_1hat{p_1} n_2hat{p_2}}{n_1 n_2}$ 为两个独立样本点估量量的加权平均数，即原假定树立的情况下，整体比率p的估量量。

Z核算量的分子是试验组与对照组比率差异的点估量，分母是测算得出的两组比率差异的标准差。

通常而言AB试验样本量满意足够，核算量t近似遵守正态分布。

4. 查验假定

在 = 0.05的条件下： $Z1−a2=1.96Z_{1-frac{a}{2}} = 1.96$ ， $Z_a = -1.6$ ， $Z_{1-a} = 1.6$

：正态分布CDF

当P值低于（等价于Z落入回绝域），则回绝原假定：组1和组2存在显着差异。

不然不回绝原假定：组1和组2不存在显着差异。

双侧查验	右单侧查验	左单侧查验
假定	H₀:p₁ = p₂ H₁:p₁ ≠ p₂	H₀:p₁ ≤ p₂ H₁:p₁ > p₂	H₀:p₁ ≥ p₂ H₁:p₁ < p₂
回绝域	\|Z\| > Z_1-/2	Z ≥ Z_1-	Z ≤ Z
P值	2-2(\|Z\|)	1-(Z)	(Z)
P值决策	P_值 < , 回绝H₀

2.5. 单侧查验or双侧查验

双侧查验因为关于查验的正负向没有假定，符合实践工作中的大多数场景，即试验作用的方向在做试验之前并不确认，因而最常被运用。

因为双侧查验大于（小于）0的回绝域被包含在右（左）单侧查验的回绝域中，因而若双侧查验正（负）向显着，必有右（左）单侧查验显着。反之若单侧查验显着，不一定有双侧查验显着。因而双侧查验更为严厉（更难显着）。

假如有很强的事务逻辑支撑试验组有正向收益，则可挑选单侧查验，不然最好挑选双侧查验。

三、最小样本量测算

3.1. 根本流程

假定查验依据小概率事情思维，确保当试验自身无收益时，咱们误判为有收益的概率很低（即约束了犯第一类过错的概率），确保了定论的稳健性。

但要怎么约束犯第二类过错的概率，即当试验存在实在收益时，咱们怎么确保收益能以较大概率（即核算成效 1-）被假定查验判定为显着？

答案是需求测算一个最小样本量，只要当样本量高于这一最小值时，试验才干到达应有的“活络度”。根本流程为：

MDE（Minimal Detectable Effect）：最小可检测单位

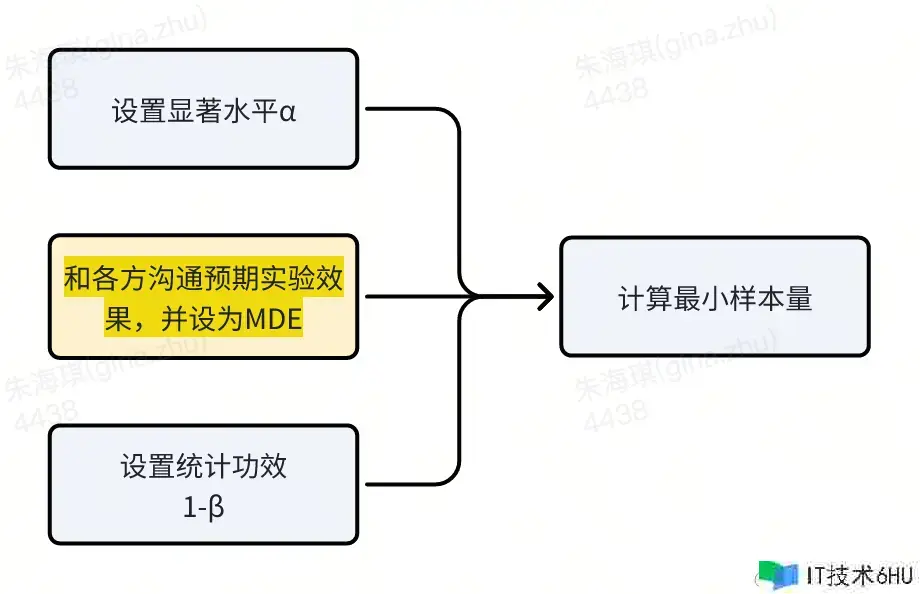
3.2. 根本概念

1. 核算成效

1-（为第二类过错的概率） 称为核算成效，表明不犯第二类过错的概率。其事务意义是当试验组和对照组存在差异，咱们依据假定查验成果判别两组存在显着差异的概率。通常来说需求设置核算成效为0.80，确保咱们有满意高的概率得到显着的定论。

核算成效和样本量、试验作用的关系：

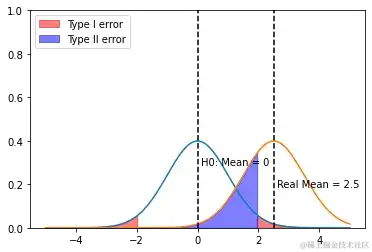
如下图所示，蓝色曲线（左）为H0为真时核算量的概率密度函数，橙色曲线（右）为核算量实践的概率密度函数，能够看到核算量实践均值大于0，即试验的干涉作用为正。赤色区域为回绝域。则蓝色区域的面积 = （核算量不落入回绝域的概率）。

能够发现，在不变时：

方差越小，越小，核算成效越大（左图->中间图后，均值之差不变，方差缩小，蓝色区域变小）；
干涉作用越显着，越小，核算成效越大（左图->右图后，均值变大，方差不变，蓝色区域变小）；

干涉作用显然不是AB试验自身能左右的。因而若想提高AB的核算成效，只要下降方差。而若想下降方差，最直接的办法只要添加样本量（另一种办法是运用方差减缩技术，本系列后续将会介绍，本文不做展开）。

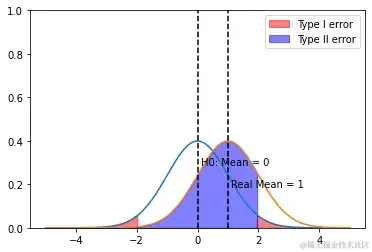
图一

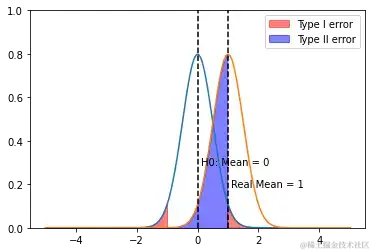
图二

图三

图一：初始条件下，较大

图二：干涉作用（核算量均值）不变，方差缩小 –> 变小

图三：差不变，干涉作用（核算量均值）变大 –> 变小

2. MDE（Minimal Detectable Effect）

最小可检测作用，也称最小可检测单位。是在给定显着水平（） 、核算成效（1-） 、总样本量（n）、试验组对照组份额（K） 的情况下，试验所能检测出来的试验组和对照组之间的最小差异：MDE越小，试验越活络。

MDE由、、n、k共同决议，能够由公式推导出来，本系列其他文章将会具体介绍，本文不作展开。

当干涉作用小于MDE时，试验不显着的概率会高于，核算成效低于1-。因而： 事务 预期收益（即事务预期的干涉作用）有必要 >= MDE，不然即便实在收益 = 事务预期收益，核算成效也达不到1 – ，或者说有＞的概率得不到显着的定论。

3.3. 最小样本量核算

在给定显着水平（） 、核算成效（1-） 、试验组对照组份额（K） 条件下，咱们需求确认最小样本量 n，使得MDE = 试验预期收益（预期收益需求和各方交流确认）。

也能够这么看，在给定显着水平（） 、MDE（=试验预期收益）、试验组对照组份额（K） 条件下，咱们需求确认最小样本量n，使得试验核算成效 = （1-） 。

1. 均值型目标

A表明试验组，B表明对照组

K表明试验组和对照组样本份额

$_A$ 表明预估试验组均值， $_B$ 表明预估对照组均值， $_A-_B$ 表明MDE

Z_x表明标准正态分布x分位数

$n_A$ 表明核算得到的试验组最小样本量， $n_B$ 表明核算得到的对照组样本量

为预估的试验组、对照组标准差（对应于上文均值假定查验中的s）

参阅：powerandsamplesize.com/Calculators…

2. 比率型目标

A表明试验组，B表明对照组

K表明试验组和对照组样本份额

$p_A$ 表明预估试验组比率， $p_B$ 表明预估对照组比率， $p_A-p_B$ 表明MDE

Z_x表明标准正态分布x分位数

$n_A$ 表明核算得到的试验组最小样本量， $n_B$ 表明核算得到的对照组样本量

参阅：powerandsamplesize.com/Calculators…

3.4. 实践工作流程参阅

假定试验为订单id随机分流。以两样本单侧查验，na = nb为例（即参数k为1，若流量分配不同，可调整参数k）：

一般设为0.05，核算成效（1-）为80%
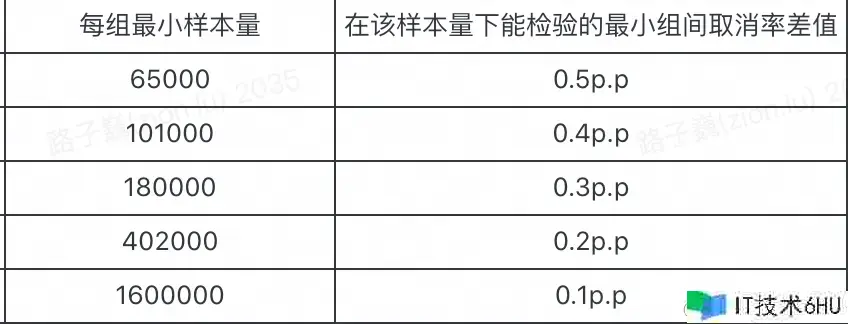
确认首要目标，例如撤销率，在试验开始前的平均水平，即对照组目标pa。例如大车东莞物理车型试验前，撤销率在35%左右。
和事务侧进行交流，估量本次试验的估计收益规模，例如估计撤销率下降0.1p.p-0.5p.p.，试验组目标pb估计处在 34% – 34.5%之间。可考虑制造如下模拟运算表知会事务方：

和事务方交流哪些城市可做试验，运用潜在试验城市的日均单量估算，多长时刻的试验所到达的样本量能够支撑多大的MDE。

3.5. 最小样本量核算东西（G*Power）介绍

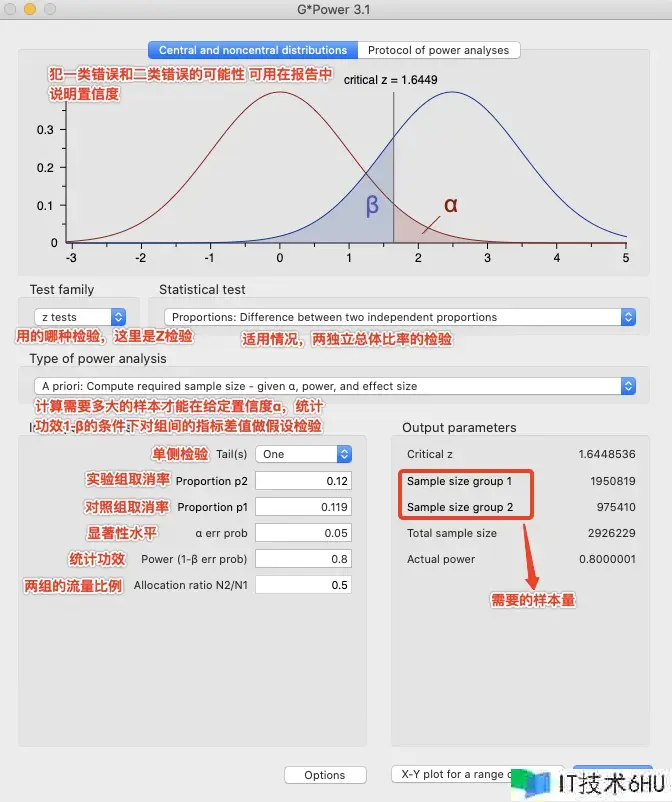
最小样本量核算较复杂，实操过程中咱们能够运用G*Power东西辅佐进行样本量核算。

1. 运用场景

A priori：已知试验组对照组目标，想知道需求多大的样本才干在确保核算成效的前提下做假定查验
*Compromise：给定试验组对照组目标和样本量，想知道和的比值，不常用
Criterion：想知道在给定核算成效，试验组对照组目标和样本量的前提下，显着性水平是多少
Post hoc：想知道在给定显着性水平，试验组对照组目标和样本量的前提下，核算成效是多少，一般用来估量在没有到达最小样本量就进行假定查验时，犯第二类过错的概率。
Sensitivity：给定，，和样本量，核算MDE

2. 根本运用办法：

2.1 主界面

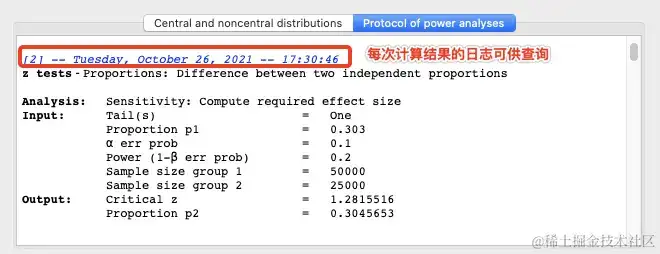
2.2 核算日志

2.3 按目标分类的各类查验目录

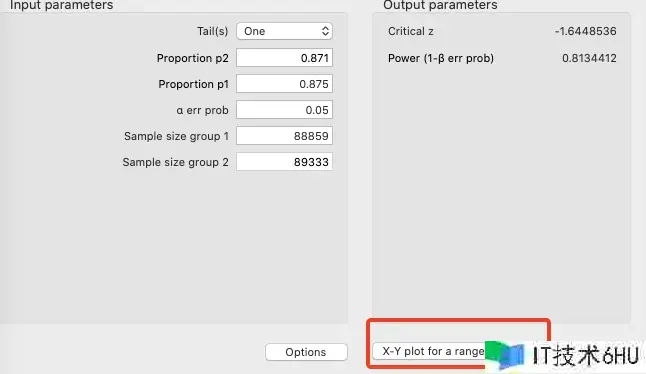
2.4 相关目标可视化

填好参数后点击”X-Y plot for a range of values”

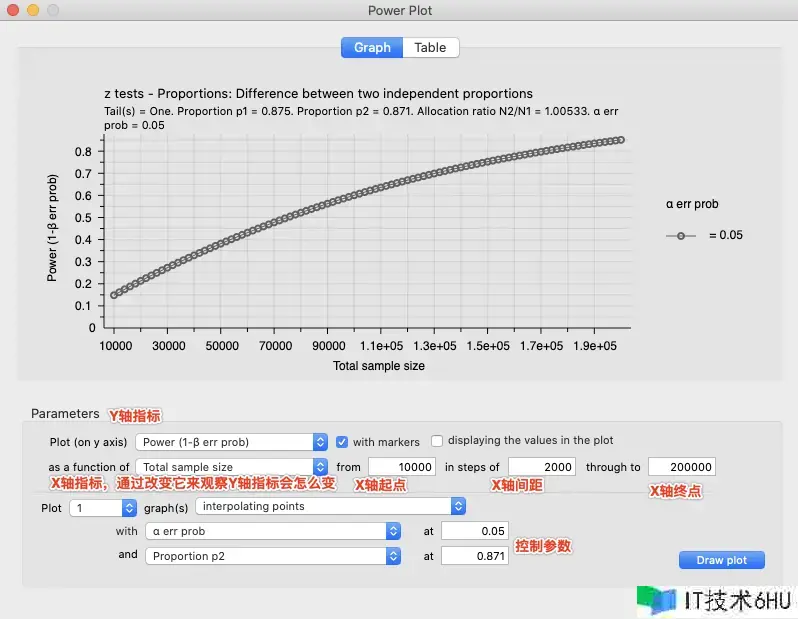
填入需求观察的信息，点击Draw plot

四、结语

本文介绍了较多AB试验中的核算学概念，以及怎么正确运用假定查验、最小样本量办法，确保试验的科学性。

一个科学的AB试验能够让咱们以客观中立的视角看待数据，评价、挑选出最好的策略，以满意货运双方市场中不同行业人群的需求。

经过本文若能树立一个对AB试验虽根底但正确的认知，也将对后续深入了解货拉拉数据科学组AB试验白皮书系列中更为进阶的内容大有帮助。

AB实验统计学基础：假设检验和最小样本量

一、评论规模

二、假定查验

2.1. 根本流程

2.2. 根本概念

2.3. 两整体均值的假定查验

2.4. 两整体比率的假定查验

2.5. 单侧查验or双侧查验

三、最小样本量测算

3.1. 根本流程

3.2. 根本概念

3.3. 最小样本量核算

3.4. 实践工作流程参阅

3.5. 最小样本量核算东西（G*Power）介绍

四、结语

作者信息

AB实验统计学基础：假设检验和最小样本量

一、评论规模

二、假定查验

2.1. 根本流程

2.2. 根本概念

2.3. 两整体均值的假定查验

2.4. 两整体比率的假定查验

2.5. 单侧查验or双侧查验

三、最小样本量测算

3.1. 根本流程

3.2. 根本概念

3.3. 最小样本量核算

3.4. 实践工作流程参阅

3.5. 最小样本量核算东西（G*Power）介绍

四、结语

相关文章

正则表达式：使用、原理和优化

Jetpack从入门到几乎入门（四）

ffmpeg使用指南

使用 LangChain 开发 LLM 应用（1）：简介

作者信息