前言

在写这篇博客之前，我其实现已写过一些关于JS递归方面的常识点了。但是我并不是为了赚这么点儿掘力值而水文，所谓温故而知新，可以为师矣，由于我对递归的认识又有了新的了解，所以撰文与咱们分享最近的学习心得。

递归的介绍

什么是递归（Recursion）？递归便是函数自己调用自己，递归有两个有必要的要求，其中一个要害是大的问题可以划分成子问题处理（即把问题的规划缩小），另外一个要害是，得是问题有必要有停止条件。

假如缺少了上面的任何一个条件，都会构成最大仓库调用的错误。

递归的运用场景十分广泛，在深度优先遍历，回溯，分治的算法规划时，根本上都是可以运用递归处理的（所以咱们经常时不时就能听到回溯递归，分治递归这样的词）。

递归有个显着的优势便是思路简略，咱们只需求把递推联系找到，就能解题。比方在做一些动态规划（递归的逆进程）算法题的时分，我归于比较笨的那种类型的人，把状况搬运方程（不知道的同学就把它了解成递推式就可以了）找到了有些时分也不太会写动态规划，哈哈，那就结合把某次递归的成果记下来的优化方法，用递归也能解题。

但是递归有个问题便是内存占用大，假如你是资深Leetcode选手，那你必定知道的事儿便是：假如某题不是有必要只能用递归才干处理的问题的话，那么规划的算法运转功率内存的开支远低于该题一切提交的平均水平。

比方，运用递归求斐波纳契数列，斐波那契数列直接便是给出的是一个递推联系，所以用递归来写的话，几乎便是手到擒来。f(n) = f(n-1)+ f(n-2)，其中f(1)=1，f(2)=1。

function fibonacci(n) {
    if(n <= 2) {
        return 1;
    } else {
        return fibonacci(n-1) + fibonacci(n-2)
    }
}

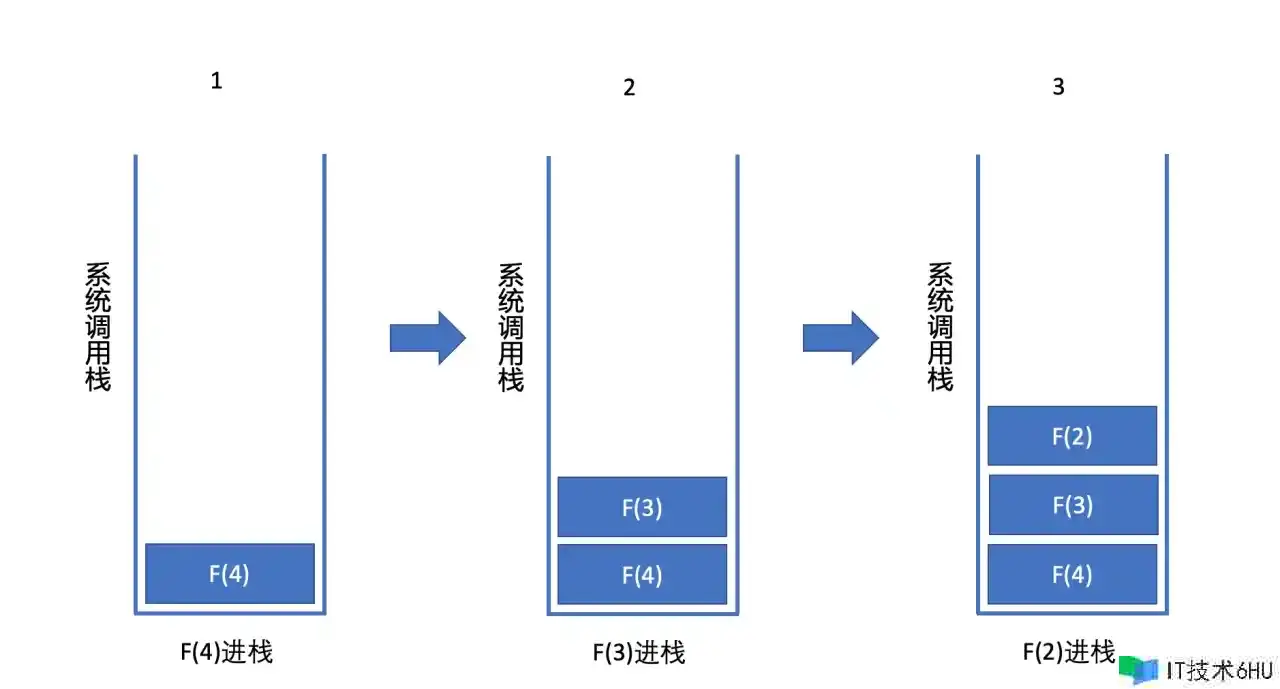
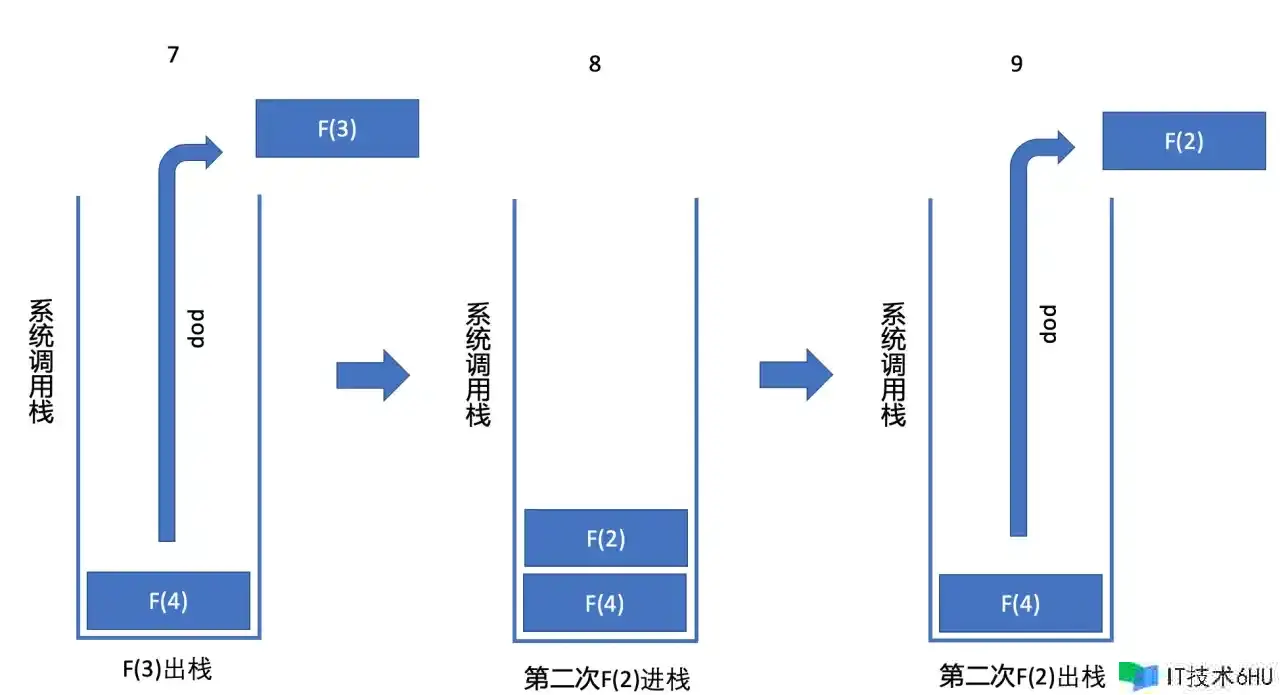
上面的这个函数履行起来是十分慢的，假设咱们要求f(5)，首要要求得f(5)，就有必要求得f(4)和f(3)，由于递归调用，所以JS引擎进入到f(4)，要求f(4)，有必要要求f(3)和f(2)，留意，之前还有个f(3)还没有求得呢，此时又开端求f(3)了，显着看到这儿发生了重复核算。好吧，那先不论，先求这个f(3)吧，求这个f(3)又需求求f(2)和f(1)，好了，f(2)和f(1)可以直接知道，所以，f(3)的值跟f(2)（求f(4)发生的f(2)，不是求f(3)的那个f(2)）现已知道了，那么f(4)就可以求得了，好了，此时又开端求最开端咱们说到的f(3)，这个进程就不给咱们解释了。经历了这么艰辛的进程，才求得了f(5)。

这是我之前写关于算法的章节，画的一个求f(4)的履行栈示意图, 履行进程大致如下：

JS的事情循环与递归

为什么分明在讲递归，却切换到了给咱们聊事情循环呢，这便是实践开发的场景了。

你有没有思考过，为什么有些团队在运用定时器的时分不允许运用setInterval而有必要要运用setTimeout+递归调用的方法，有些时分是没有任何退出的条件的递归，那为什么浏览器没有卡死呢？这不看起来就跟咱们在文章最初说到的递归的两个要害点对立吗？不，不对立，其实不是一回事儿。

比方这段代码：

function test(i) {
  requestAnimationFrame(() => {
    console.log(i++);
    test(i);
  });
}

JS的调用栈，其实你可以把它了解为它仅仅是相关在一个履行上下文中的（这是我自己的了解，非官方论述），假如你一向往这个栈里边添加内容，在有限的栈长度下，终究肯定会爆栈。

之前，在抖音短视频里边看到过渡一讲师袁进教师说现在Chrome浏览器的使命行列现已有好几种优先级的了，但是我没有研究过，而且用咱们不熟悉的方法论述不便于咱们的了解，因而，下文仍然以宏使命行列和微使命行列的提法来论述。

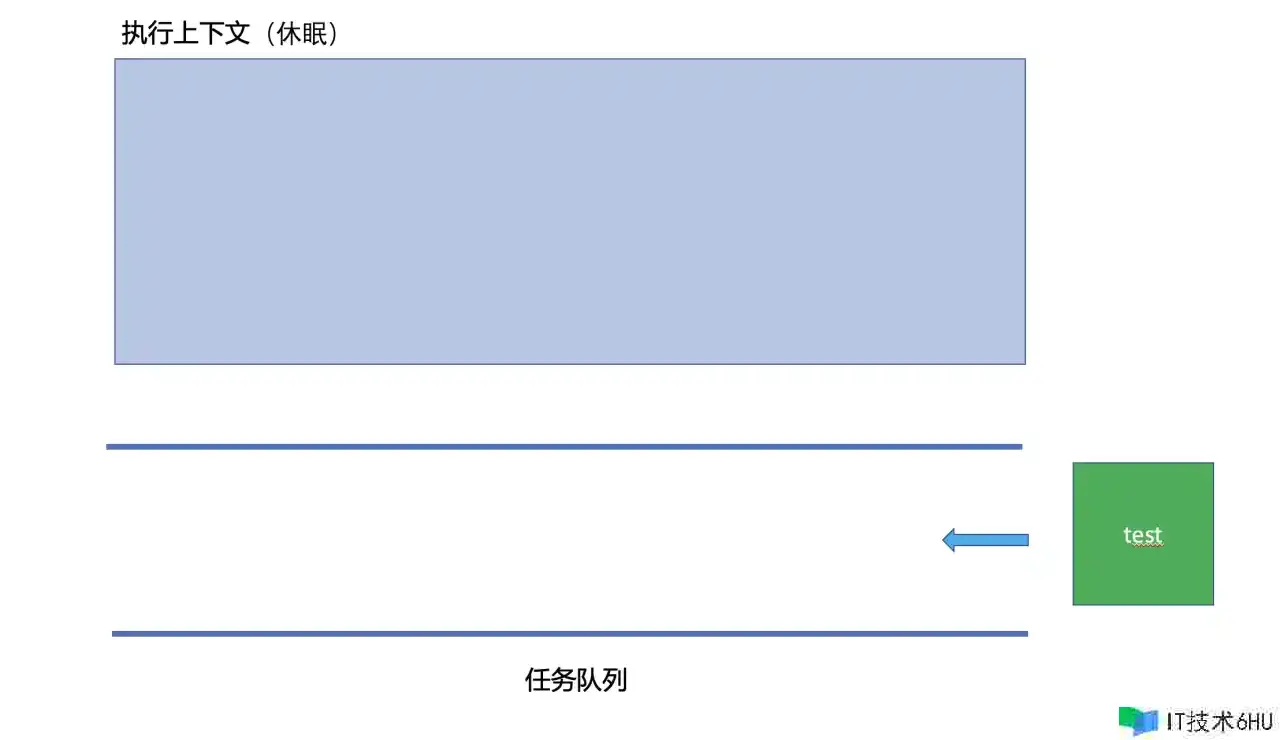
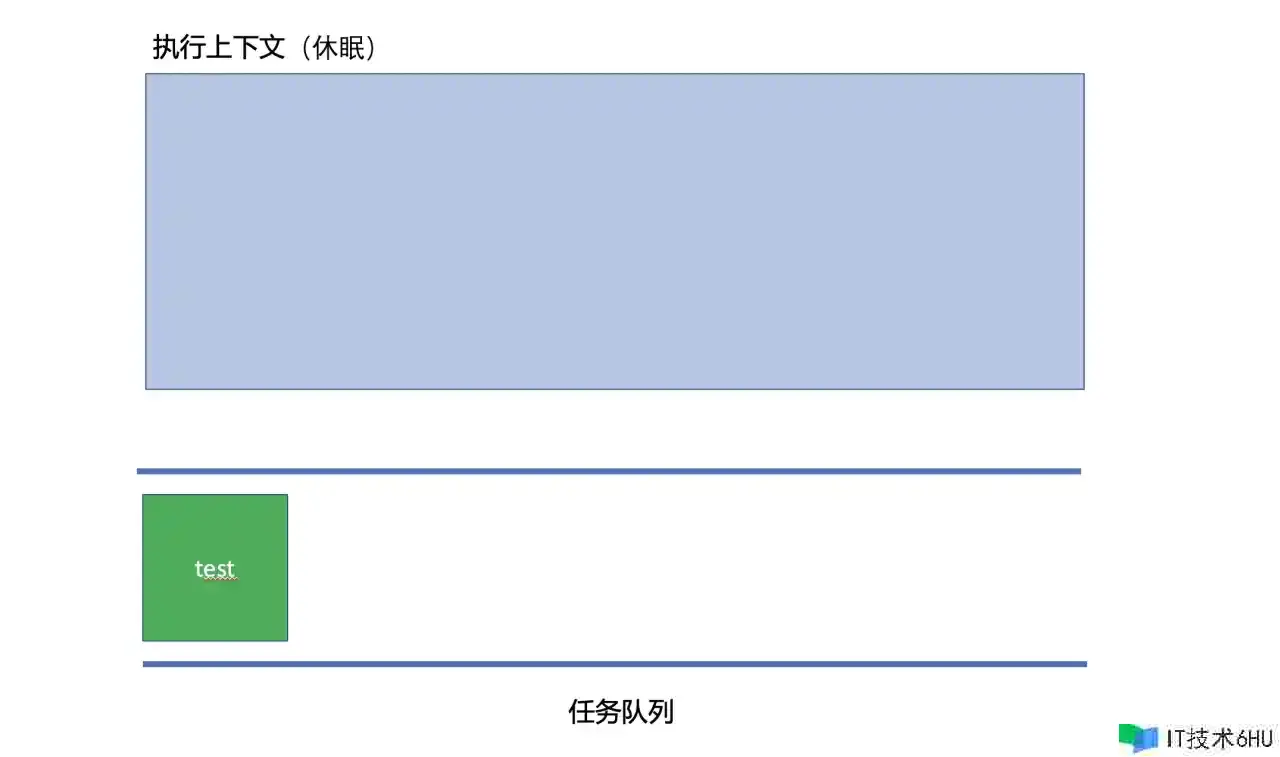
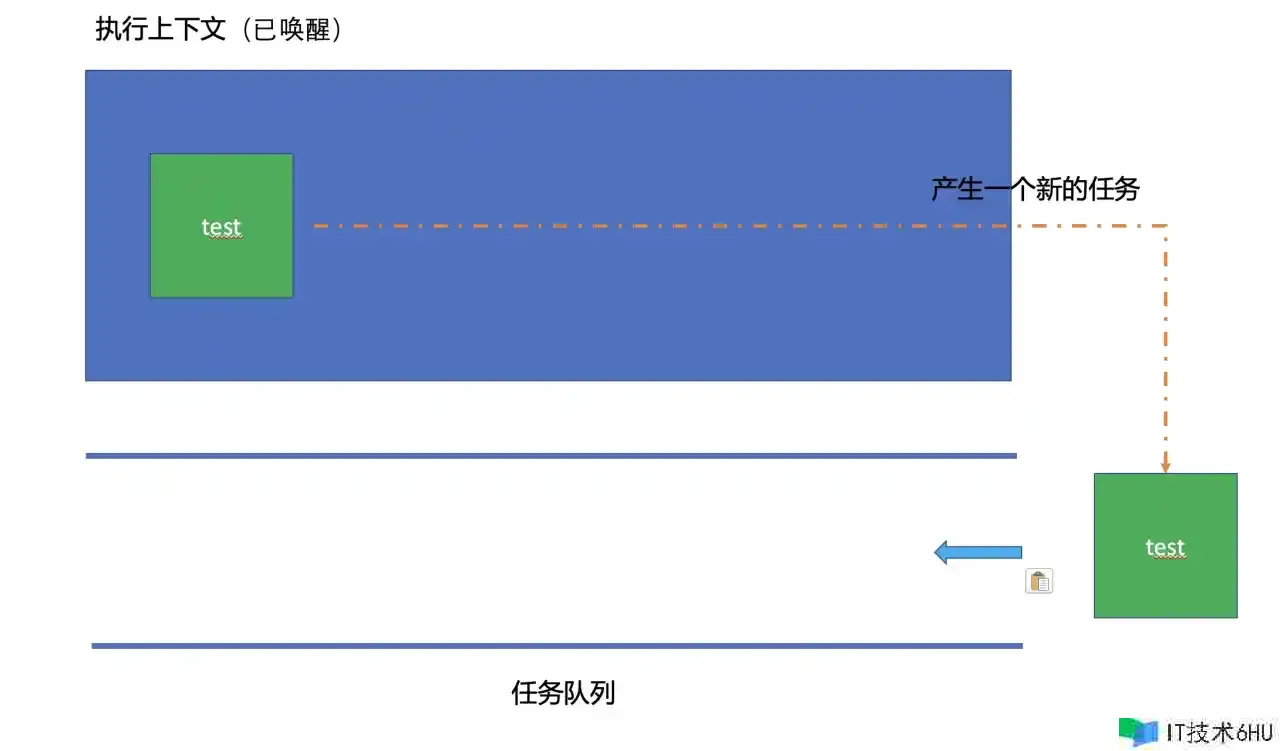
基于requestAnimationFrame(setTimeout，setImmediate，Promise，async函数)的递归调用，其实它的履行流程是这样的，JS其实是有一个使命行列（其实有许多个使命行列，如微使命行列，定时使命行列等，咱们在谈论这个地方时分可以不用关心那么多行列，所以就只谈论一个使命行列就好），首要假如这个使命行列中没有使命，那么JS主线程就休眠，当这个以为行列里边有内容的时分，JS主线程就取消休眠，而且从使命行列中取出一个使命来处理（这便是所谓的同步使命），但是，一个同步使命中，又有或许加入新的使命到使命行列中去，之前的requestAnimationFrame函数内递归调用了test函数，就发生了一个新的使命追加到了使命行列里边去，所以，这个递归操作其实导致的成果，是使得JS的主线程每时每刻都有活儿干，而并不会发生最大仓库调用的错误。

这个特性是JS语言自身的特性，开发者需求尤为留意。

以下是test函数的履行流程：

比方下面这段代码，它便是一向在微使命行列里边添加内容，假如咱们把数组的内容设置的特别长的话，尽管不会爆栈，但是这会导致浏览器看起来卡死了。

console.log('sync script execution');
const list = Array.from({ length: 100000000 }).map(_ => ({}));
async function fn() {
  const node = list.shift();
  console.log(node);
  while (list.length) {
    await fn();
  }
}
fn();
setTimeout(() => {
  console.log('set timeout execution')
}, 0)

操控台首要打印一下sync script execution，然后就一向开端输出空目标内容，此时假如咱们点击页面元素的话，页面没有任何反响，开发者东西也关闭不了，这是由于咱们一向不断的在往浏览器微使命行列里边刺进内容，当微使命行列的内容不空的话，就无法开启下一轮事情循环，而咱们的操作适当于便是把它放到了宏使命行列里边去等待履行，所以在将来的某一刻，浏览器会呼应咱们的操作。终究，当微使命行列处理完结之后，浏览器打印set timeout execution，咱们的浏览器就卡过了。

所以，但凡跟异步打交道的递归调用，都不能严厉意义上的称为递归，它仅仅是看起来像是递归算了。

递归的优化

关于递归的优化，是本文重点向咱们论述的内容，由于我也是看了一些书籍材料后有了新的了解，这也是我为什么要发这篇文章的原因。

缓存

在核算斐波纳契数列的时分，就现已跟咱们提过了，之前的实现进程中，咱们进行了大量的重复核算，因而，可以把现已核算过的成果保存下来，然后用到的时分直接回来，防止屡次核算。

咱们针对前文说到过的斐波那契数列的比方进行改写。

function fibonacci(n, map = new Map()) {
    // 发现现已核算过了，则不再重复核算
    if(map.has(n)) {
        return map.get(n);
    }
    if(n <= 2) {
        return 1;
    } else {
        const subVal1 = fibonacci(n-1, map);
        const subVal2 = fibonacci(n-2, map)
        const sum = subVal1 + subVal2
        // 缓存成果，供后续运用
        map.set(n, sum);
        return sum;
    }
}

有的同学会说，为什么上面的写法，不把subVal1也用Map记载下来呢？没必要，由于在履行fibonacci(n-1, map)这行代码的时分，假如说事前现已缓存了成果的话，其实再履行一次它就适当所以一次很高效的操作，假如没有的话，那还不是一样需求履行，所以只需求在终究缓存一下核算成果即可。

尾递归优化

关于尾递归的优化，也是面试中常考的一个问题，这也便是我撰写这篇博客的原因。

尾递归的概念

尾递归调用是函数式编程的一个重要概念，自身十分简略，一句话就能说清楚，便是指某个函数的终究一步是调用另一个函数。

以下三种方法都不是尾递归调用：

// 状况一
function f(x){
  let y = g(x);
  return y;
}
// 状况二
function f(x){
  return g(x) + 1;
}
// 状况三
function f(x){
  g(x);
}

我个人的了解便是，说白了，便是return语句后边跟上一个光溜溜的函数调用，适当于不依靠当前作用域下面的某些参数，其函数的入参可以直接被记载下来，在适宜的时分可以当一次一般的调用那个return语句后边的函数的那种感觉。

这个思维很重要，之后的一个章节的优化就需求围绕这个了解打开。

以下内容是完全摘录自阮一峰教师的ES6网络博客：

函数调用会在内存构成一个“调用记载”，又称“调用帧”（call frame），保存调用方位和内部变量等信息。假如在函数A的内部调用函数B，那么在A的调用帧上方，还会构成一个B的调用帧。比及B运转完毕，将成果回来到A，B的调用帧才会消失。假如函数B内部还调用函数C，那就还有一个C的调用帧，以此类推。一切的调用帧，就构成一个“调用栈”（call stack）。

尾调用由所以函数的终究一步操作，所以不需求保存外层函数的调用帧，由于调用方位、内部变量等信息都不会再用到了，只需直接用内层函数的调用帧，取代外层函数的调用帧就可以了。

但是，我个人觉得还算是说的比较玄幻。然后我就和一位曾经上任过腾讯的搭档交流了一下，他厚实的技能储备使我十分钦佩，我觉得他的了解方法要简略许多。

所以，从我搭档的解释来说，就像我上文说的一样，尾递归就像咱们把这个函数调用的一切参数记载下来，然后在适宜的机遇把这个函数当一般的函数调用一下。假如说不是尾递归，那么需求依靠之前的作用域下面的变量，那引擎就无法做优化了。

但是，问题便是，我觉得十分古怪的事儿，我依据咱们说到的尾递归优化的写法，编写了代码来履行，但是却没有呈现我预期的尾递归优化的作用。

首要，咱们把之前说到过的求斐波拉契数列的函数写成尾递归的方法。

function fibonacci2 (n , ac1 = 1 , ac2 = 1) {
  if( n <= 1 ) {
      return ac2
  };
  return fibonacci2(n - 1, ac2, ac1 + ac2);
}

关于非尾递归改写成尾递归，我个人的经历便是在原函数的参数上做文章，使得可以把上次的核算成果可以传递给下一次核算，假如一个函数里边有多个递归调用，则无法改写成尾递归，比方快速排序，递归遍历二叉树

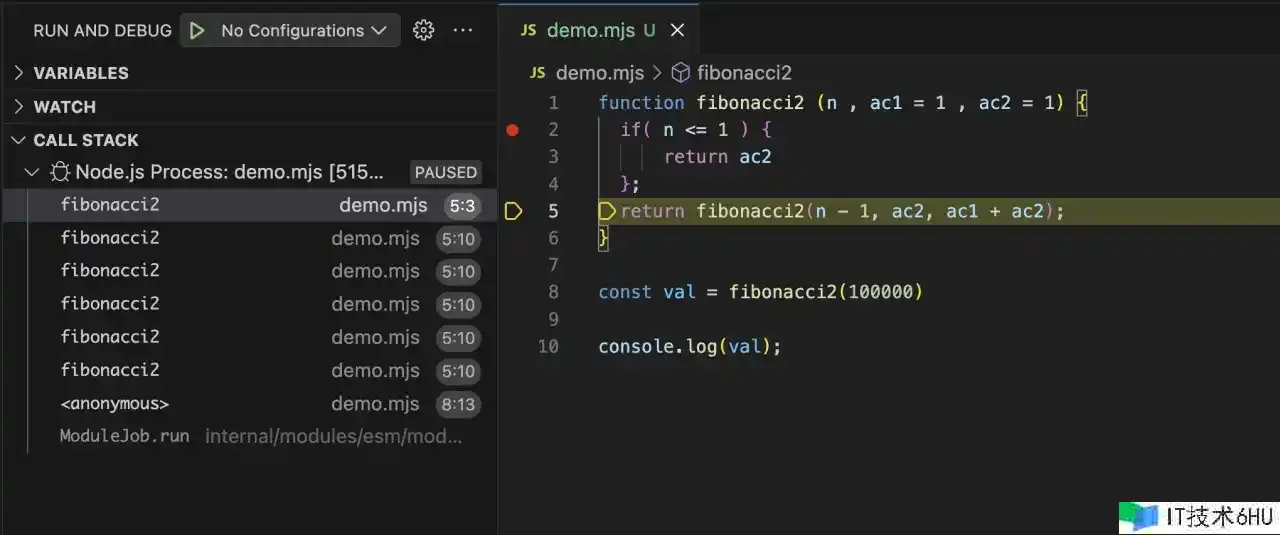
我首要用Node 16履行一个很大的数据，但是并没有看到仓库的优化：

我把这个代码拿到浏览器立马再试一下：

仍是不行（我所用的浏览器是Edge浏览器），终究再用谷歌浏览器试一下，也是一样的成果。

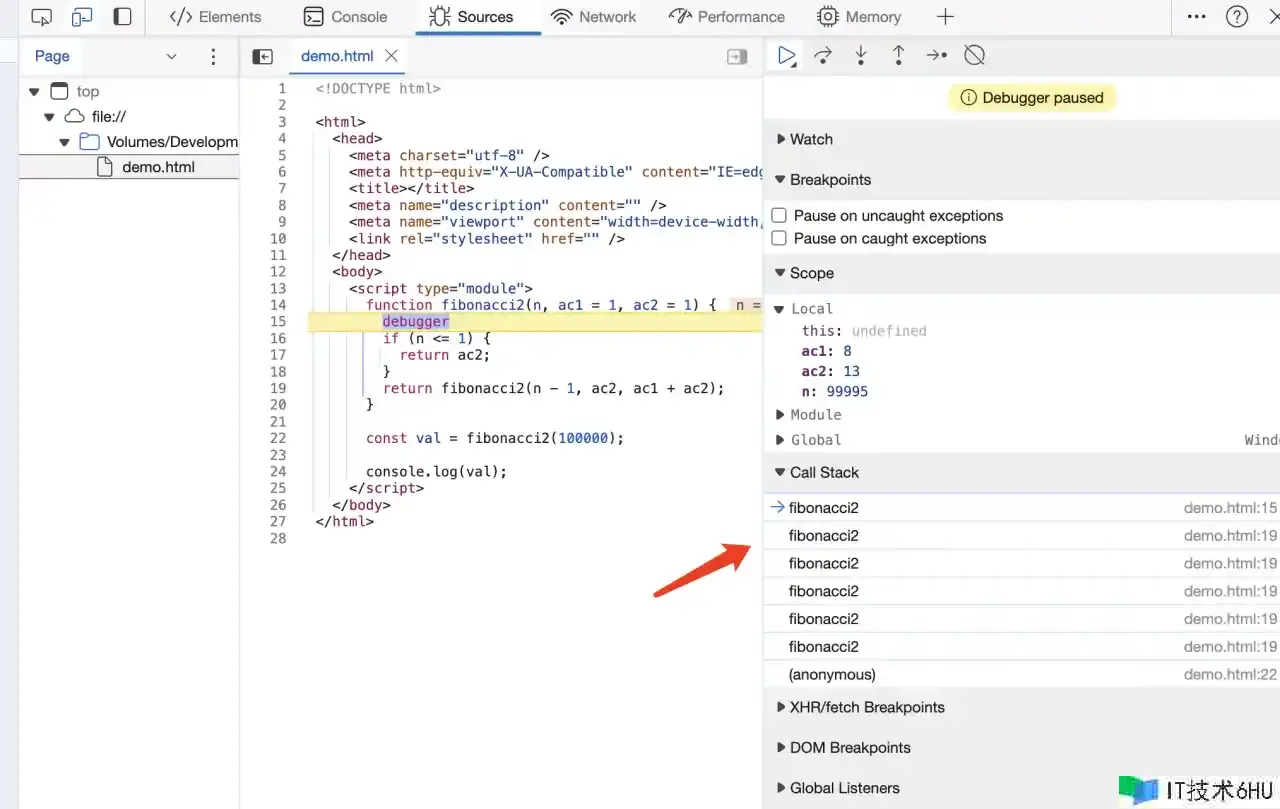
方才，咱们说到了，由于尾递归不用考虑对外界的变量的依靠，那假设咱们把这些变量存起来，然后把这些变量当一个循环来履行函数不就行了吗？

就算引擎不支持优化，那咱们也可以采用编程的手法来进行操控，下一节主要就论述运用编程的手法进行尾递归优化。

蹦床函数

蹦床函数的实现思路是这样的，当递归进行的时分，事务函数的回来值是自身的调用，那就可以接着循环，假如某个时间的回来值对错函数类型时，就说明递归现已进行完结。

以下便是本文要说到的(下面这个蹦床函数摘录自阮一峰教师的ES6网络博客)

function trampoline(f) {
  while (f && f instanceof Function) {
    f = f();
  }
  return f;
}

咱们把之前写的尾递归核算斐波那契数列的函数改写成蹦床函数优化的方法：

function trampoline(f) {
  while (f && f instanceof Function) {
    f = f();
  }
  return f;
}
function fibonacci2 (n , ac1 = 1 , ac2 = 1) {
  if( n <= 1 ) {
      return ac2
  };
  // 本来是回来值，改写成回来一个函数，这样蹦床函数能知道递归还没有完毕
  return () => fibonacci2(n - 1, ac2, ac1 + ac2);
}
const fibVal = trampoline(fibonacci2.bind(null, 1000))
console.log(fibVal);

可以看到，上面的这个蹦床函数用起来仍是比较难受的，假如说把它写成像lodash的debounce这样的高阶函数那样的话，用起来就比较友好了，所以，咱们对其进行重构。

type Func<T, V> = (...args: T[]) => V | Func<T, V>;
function trampoline<T, V>(fn: Func<T, V>) {
  return function trampolined(...args: T[]) {
    let result = fn.bind(null, ...args);
    while (typeof result === "function") {
      result = result();
    }
    return result as V;
  };
}

然后，咱们需求这样运用就可以了：

function fibonacci2 (n: number, ac1 = 1 , ac2 = 1) {
  if( n <= 1 ) {
      return ac2
  };
  return () => fibonacci2(n - 1, ac2, ac1 + ac2);
}
const fib = trampoline(fibonacci2);
const fibVal = fib(1000);
console.log(fibVal);

经过这种方法封装之后，更靠近咱们的实践开发。

真正的尾递归优化

蹦床函数是一种优化方法，而且蹦床函数的优化需求咱们改写本来的事务逻辑（本来的逻辑是回来成果便是递归体，需求改写成回来函数，在这个函数中履行递归体），此外阮一峰教师的网络博客里边还给出了一个真正的尾递归优化方法，这种方法咱们就不需求调整任何事务逻辑代码了。

function tco(f) {
  var value;
  var active = false;
  var accumulated = [];
  return function accumulator() {
    accumulated.push(arguments);
    if (!active) {
      active = true;
      while (accumulated.length) {
        value = f.apply(this, accumulated.shift());
      }
      active = false;
      return value;
    }
  };
}

这个函数的理论基础便是我在前文说到的我对尾递归的了解，由于不需求依靠上次调用的变量，咱们只需求把参数记载下来，作为一次一次的循环调用。

不过这个函数的思路出奇的惊奇，我依据自己的了解，解释一下它的履行流程。

定义一个符号，主要是用来操控履行，由于一旦开端履行，函数其实是像上文说到的是用前面的成果替换后边的成果。

所以，accumulator函数进来，先把第一次的函数参数添加到参数数组记载里边去，此时，符号仍是false，可以进入到循环流程，然后它履行到了if里边的逻辑就立刻把符号设置成了true，好了，这样就适当于过河拆桥了。

现在，它先履行本次调用的成果，所以从参数列表里边取出一个成果开端履行，而且将回来成果设置给value。

但是问题便是，本次履行是一个递归调用，之前的第一次履行，现已把桥拆了，递归调用accumulator就只能把参数都添加到参数数组记载里边去了，这就导致了参数数组的length又不0了，这样while循环就能履行到递归调用完毕了，而且，每次履行都把上一次的履行成果给替换掉。

当递归履行完结的时分，把符号初始化，就比方把桥从头搭好，下次调用的时分，又可以重复这样的进程。

运用tco函数来履行一下咱们之前尾递归调用方法的斐波拉契数列：

function tco(f) {
  var value;
  var active = false;
  var accumulated = [];
  return function accumulator() {
    accumulated.push(arguments);
    if (!active) {
      active = true;
      while (accumulated.length) {
        value = f.apply(this, accumulated.shift());
      }
      active = false;
      return value;
    }
  };
}
function fibonacci2 (n , ac1 = 1 , ac2 = 1) {
  if( n <= 1 ) {
      return ac2
  };
  return fibonacci2(n - 1, ac2, ac1 + ac2);
}
const fib = tco(fibonacci2);
const fibVal = fib(1000)

递归转动态规划

递归转动态规划这一章节归于帮助对算法还不太了解的同学拓宽常识面的一个末节。

递归处理问题的进程中，咱们可以看到，终究始终是要回归到最小问题解的。

那已然需求一步一步的拆分问题，然后求得这些子问题的解之后，终究还需求把这些子问题的解兼并成终究的答案。那为什么咱们纷歧开端就直接从子问题开端求解，然后直接将子问题兼并成终究问题的解呢？

所以直接从子问题推导出终究答案的解题进程，这种处理问题的算法就叫做动态规划（Dynamic Programming），咱们一般简称DP。

动态规划在核算进程中，从子问题的解推导出总问题的逻辑联系，咱们称之为状况搬运方程式，但是问题便是在于这个状况搬运方程式十分难以推导，所以许多的程序员都觉得它难（我也不例外）。

以下就向咱们展现运用动态规划的方法求斐波那契数列的方法：

function fibonacci3(n) {
    let ac1 = 1;
    let ac2 = 1;
    // 初始化为1，由于，第一项和第二项都是1，在循环一次都不履行的时分，确保回来值总是正确的
    let sum = 1;
    for(let i = 3; i<=n; i++) {
        // 现已求得了本次的成果
        sum = ac1 + ac2;
        // 由于斐波那契数列只需求最近的两个值，所以，远一点儿的那个值就可以丢掉了
        // 将ac2赋值给ac1，这个操作就像是丢掉掉较远的那个值
        ac1 = ac2;
        // 将sum赋值给ac2，使得最近的两个数值都操纵咱们预期的作用，以便于可以求得下一次的成果
        ac2 = sum;
    }
    return sum;
}

不过，需求留意的一点是，不是一切的问题都可以运用动态规划。动态规划常用于求解具有以下特征的问题：

最优子结构性质（Optimal Substructure） ：问题可以分解为若干个相互独立且相似的子问题，每个子问题都有一个最优解。这意味着问题的全体最优解可以经过兼并子问题的最优解来获得。
堆叠子问题（Overlapping Subproblems） ：在处理问题的进程中，同一个子问题或许会被屡次重复求解。DP算法经过记忆化存储现已处理过的子问题的解来防止重复核算，从而提高功率。
状况搬运方程（State Transition Equation） ：问题的最优解可以经过子问题的最优解以某种方法组合得到。这种组合联系一般经过状况搬运方程来表示，描绘了问题的各个状况之间怎么相互相关。

比方遍历一个二叉树就不具有上述的特征，那肯定就不或许用动态规划来处理问题了。

总结

本文旨在向咱们论述尾递归优化，而且给出了两个尾递归优化的处理方案。

递归是实践开发中呈现频率超高的场景，但是假如你可以清晰知道这个场景可以有非递归的实现，那从一个程序员的工作素质来说，就不要运用递归。不是一切的递归都可以写成尾递归。

尤其是我跟后端搭档在谈天的时分，他们只需谈到递归第一反响便是数据的量级考量，小公司或许用户量少还好，但大公司就纷歧样了，一旦数据量超载，那成果将会是灾难性的（“又不是不能用”，抱愧，这次是真的不能用了，哈哈哈，当心p0级别的事故砸到你头上）。关于咱们前端来说根本不会有这样海量数据的事务场景，所以实践的运用心智担负倒也不是那么重。

本文也依据我在实践开发中遇到的问题，向咱们论述了异步编程下的递归与一般递归的区别，请各位读者加以领会。

终究，以递归的关键向咱们解释了动态规划的根本处理原理，有技能追求的同学可以自行钻研一下，这部分的常识点可以提高你的编程认知。

关于本文论述的内容有任何疑问的同学可以在谈论区留言或私信我。

假如咱们喜欢我的文章，可以多多点赞收藏加关注，你们的认但是我最好的更新动力，。

成为高级工程师的必经之路——你必须掌握JS递归的那些事儿

前言

递归的介绍

JS的事情循环与递归

递归的优化

缓存

尾递归优化

尾递归的概念

蹦床函数

真正的尾递归优化

递归转动态规划

总结

更多文章

评估基准在人工智能研究中的重要性

Nop入门：动态SQL管理

Android gralde 脚本迁移到 Kotlin DSL

AST-GREP：基于语法和语义的代码搜索与替换，你需要了解一下！