OpenGL ES 2.0 笔记 #7：空间变换

从 3D 场景到屏幕 2D 图画，通过了一系列空间/坐标改换才得以完成：

• Vertex Shader – 取决于 3D 建模和烘托的实践工作流程，先后进行 3 次改换。3D 模型极点坐标由本地模型坐标转化到 Clip Space
  • Model Transform（模型改换）- 3D 模型放置到 3D 场景（即：世界）
  • View Transform（视图改换）- 摄像机以特定姿势（观察视点/朝向）放置到 3D 世界的特定方位；以摄像机为参照，将 3D 世界转化到摄像机空间
  • Projection Transform（投影改换）- 由投影方式和摄像机本身的参数确认。投影方式分为正交投影和透视投影 2 种。在透视投影的情况下，确认坐标改换的摄像机参数包括：水平和竖直方向的视角（Field of View）、近景面和远景面的间隔（z）
• Rasterizer –
  • Perspective Division（透视除）- 完成 Clip Space 坐标的 normalize，即由 (x, y, z, w) -> (x/w, y/w, z/w, 1)。通过 Perspective Division 后的空间称为 NDC (Normalized Device Coordinates)
  • Viewport Transform（视口改换）- 将 NDC 映射到屏幕 Viewport 内。分解为 translate 和 scale，无 rotate

摄像机空间界说如下，特别注意朝向为 -z：

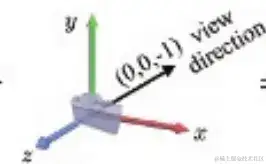
Vertex shader 完全编程完成，Rasterizer 硬件固定完成，程序只能修正部分参数，例如设置 Viewport。

OpenGL 将坐标表明为列矢量（Column Vector，即 4×1 矩阵），而不是行矢量（Row Vector，即 1×4 矩阵）；因而，改换矩阵作用于坐标要运用“左乘”，即

v' = M⋅v

若通过多次改换，改换矩阵依次为 M1, M2, M3…, Mn，则乘次序为

v' = Mn⋅...⋅M3⋅M2⋅M1⋅v

Vertex Shader 运用右手坐标（RHS），而 Rasterizer 运用左手坐标（LHS），因而，在 Vertex Shader 的最后一步要进行 RHS 到 LHS 的转化，最简略的完成是将 z 取负。

cglm 是 C 完成的用于空间改换运算的库，界说了与 OpenGL/GLSL 相兼容的 vector, matrix 类型及操作等。cglm 能够不需编译链接，只是包括头文件即可。头文件中的函数全部界说为 inline。

用 cglm 进行 3D 改换，获得改换矩阵：

#include <cglm/cglm.h>
...
mat4 m = GLM_MAT4_IDENTITY_INIT;
{
    vec3 t = {.5, -.5, 0};
    glm_translate(m, t);
    float a = (float)SDL_GetTicks() / 1000;
    vec3 z = {0, 0, 1};
    glm_rotate(m, a, z);
    vec3 s = {.5, .5, .5};
    glm_scale(m, s);
}

注意因为如前所述改换矩阵的“左乘”原则，代码中的改换次序与实践刚好相反。3D 模型原本坐落原点，首先进行 scale 缩小到一半，然后以 z 轴为中心旋转一定视点，这儿的旋转视点不固定，取决于时刻戳。最后向左下角方向平移 0.5 的间隔。

以上代码在 render() 函数内反复运转，因而呈现出滚动的作用。

转化矩阵以 uniform 供 vertex shader 拜访：

uniform mat4 m_trans;
void main()
{
    gl_Position = m_trans * a_pos;
    ...
}

程序中将改换矩阵的值复制给 uniform：

GLuint prog = ...
GLint trans_loc = glGetUniformLocation(prog, "m_trans");
glUniformMatrix4fv(trans_loc, 1, GL_FALSE, (GLfloat *)m);

cglm 的 matrix 完成为二维数组 float[4][4]，直接将首地址提交给 OpenGL。

程序运转如下。完好代码在 gitlab.com/sihokk/lear…

上一例程代码中演示了对 3D 模型的分解改换，即 scale, rotate, translate。在实践的 3D 应用中，通常依照 MVP（Model, View, Projection）的次序进行改换。以游戏为例，游戏人物的移动归于 Model 改换，玩家的视角变化归于 View 改换。下面代码进行简略的 MVP 改换：

mat4 m_model = GLM_MAT4_IDENTITY_INIT;
{
    vec3 x = {1, 0, 0};
    glm_rotate(m_model, glm_rad(-55), x);
}
mat4 m_view = GLM_MAT4_IDENTITY_INIT;
{
    vec3 v = {0, 0, -3};
    glm_translate(m_view, v);
}
mat4 m_proj;
{
    glm_perspective(glm_rad(45), render_state.screen_width / (float)render_state.screen_height, 1, 100, m_proj);
}

Model 改换将 3D 模型绕 x 轴旋转一定视点；View 改换将摄像机后移（ z 方向）3，关于 3D 模型等同于向 -z 方向平移 3。Projection 改换进行透视投影，提供摄像机参数，cglm 函数 glm_perspective() 计算出改换矩阵。

将所得 3 个改换矩阵提交给 shader：

GLuint prog = ...
GLint loc_model = glGetUniformLocation(prog, "m_model");
GLint loc_view = glGetUniformLocation(prog, "m_view");
GLint loc_proj = glGetUniformLocation(prog, "m_proj");
glUniformMatrix4fv(loc_model, 1, GL_FALSE, (GLfloat *)m_model);
glUniformMatrix4fv(loc_view, 1, GL_FALSE, (GLfloat *)m_view);
glUniformMatrix4fv(loc_proj, 1, GL_FALSE, (GLfloat *)m_proj);

在 vertex shader 中用改换矩阵乘极点坐标，进行空间转化：

attribute vec4 a_pos;
uniform mat4 m_model;
uniform mat4 m_view;
uniform mat4 m_proj;
void main()
{
    gl_Position = m_proj * m_view * m_model * a_pos;
    ...
}

注意到：左乘，且 MVP 次序为从右到左。

程序履行结果如下图。完好代码见 gitlab.com/sihokk/lear…

到上面的例程为止，我们运用的 3D 模型都是 2D 平面形体。下面将制作一个真正的 3D 模型，立方体。立方体 6 个面，每个面 2 个三角形，因而立方体一共需求 36 个极点，尽管其中大部分方位重合：

const GLfloat vertices[] = {
    -0.5f, -0.5f, -0.5f, 0.0f, 0.0f,
    0.5f, -0.5f, -0.5f, 1.0f, 0.0f,
    0.5f, 0.5f, -0.5f, 1.0f, 1.0f,
    ...
};
GLint attr_pos = glGetAttribLocation(prog, "a_pos");
GLint attr_tex = glGetAttribLocation(prog, "a_tex");
const GLsizei stride = 5 * sizeof(GLfloat);
glEnableVertexAttribArray(attr_pos);
glVertexAttribPointer(attr_pos, 3, GL_FLOAT, GL_FALSE, stride, 0);
glEnableVertexAttribArray(attr_tex);
glVertexAttribPointer(attr_tex, 2, GL_FLOAT, GL_FALSE, stride, (void *)(3 * sizeof(GLfloat)));

每个极点包括 x/y/z 方位坐标和 texture 坐标 s/t，共 5 项数据。方位坐标和 texture 坐标分别绑定到 shader attribute 变量。

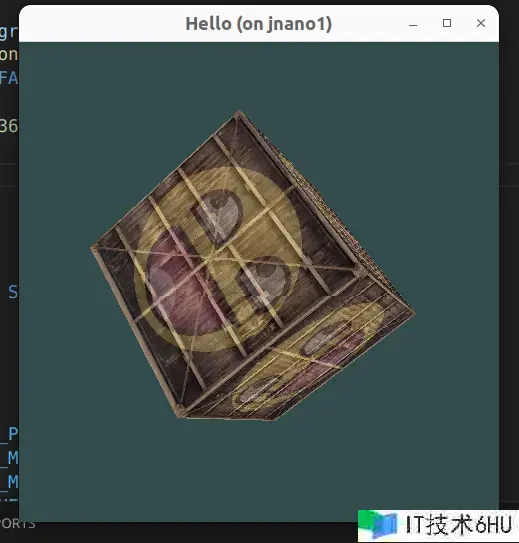
运转程序，将会发现立方体显现异常：

这是因为没有启用 OpenGL 深度测验（Depth Test）。若未启用深度测验，可能导致烘托时将原本“背面”的面制作到前台，就像上面那样。OpenGL 默许不启用深度测验。首先要在初始化时启用深度测验，其次在每次烘托一帧前都需求清除深度缓冲，如下：

static void render_init()
{
    glEnable(GL_DEPTH_TEST);
    ...
}
static void render()
{
    glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
    ...
}

另外，在创建 SDL2 OpenGL context 时，须确保支撑深度缓冲：

SDL_GL_SetAttribute(SDL_GL_DEPTH_SIZE, 8);

启用 depth test 后，立方体就能被正确制作出来：

完好代码在 gitlab.com/sihokk/lear…

留意到有个细节。在上面示例中，将 MVP 矩阵独自提交给 shader，矩阵乘实践由 shader 履行。Vertex shader 对每一个极点履行一次，有多少个极点，就要进行多少次重复的矩阵乘。这是不必要的。能够在程序中进行 MVP 改换矩阵乘，将最终结果矩阵提交给 shader：

mat4 m = GLM_MAT4_IDENTITY_INIT;
// Rotate
{
    mat4 m1 = GLM_MAT4_IDENTITY_INIT;
    ...
    glm_rotate(m1, ...);
    glm_mat4_mul(m1, m, m);
}
// Translate
{
    mat4 m1 = GLM_MAT4_IDENTITY_INIT;
    ...
    glm_translate(m1, ...);
    glm_mat4_mul(m1, m, m);
}
// Projection
{
    mat4 m1;
    glm_perspective(..., m1);
    glm_mat4_mul(m1, m, m);
}
GLuint prog = ...
GLint loc = glGetUniformLocation(prog, "m_trans");
glUniformMatrix4fv(loc, 1, GL_FALSE, (GLfloat *)m);

注意矩阵乘 glm_mat4_mul() 的参数的次序，以及 MVP 的次序！

Vertex shader 直接将改换矩阵应用到极点坐标：

uniform mat4 m_trans;
void main()
{
    gl_Position = m_trans * a_pos;
    ...
}

这次用一个 for 循环制作 10 个立方体。实践是同一个 3D 模型，通过不同的空间改换制作 10 次，例如不同的挑选视点、放置在不同方位，等等。程序运转作用如下：

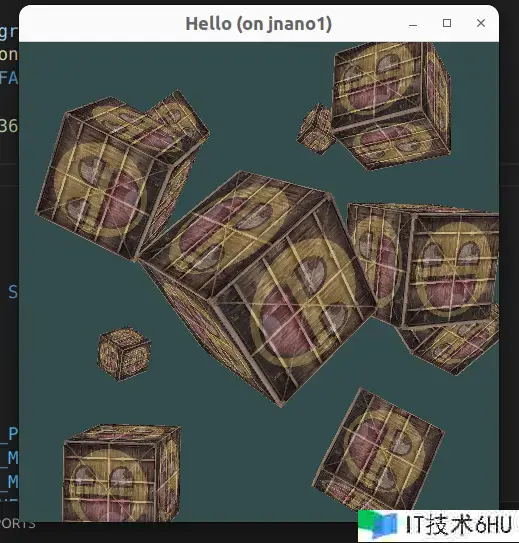
程序代码在 gitlab.com/sihokk/lear…