使用分形思想，通过图灵完备的机器赛跑关卡，并获得小机快跑成就-六虎

本文作者：Wyu-Cnk

本年咱们定制了六款红包封面，欢迎领取

运用微信扫码领取

前语

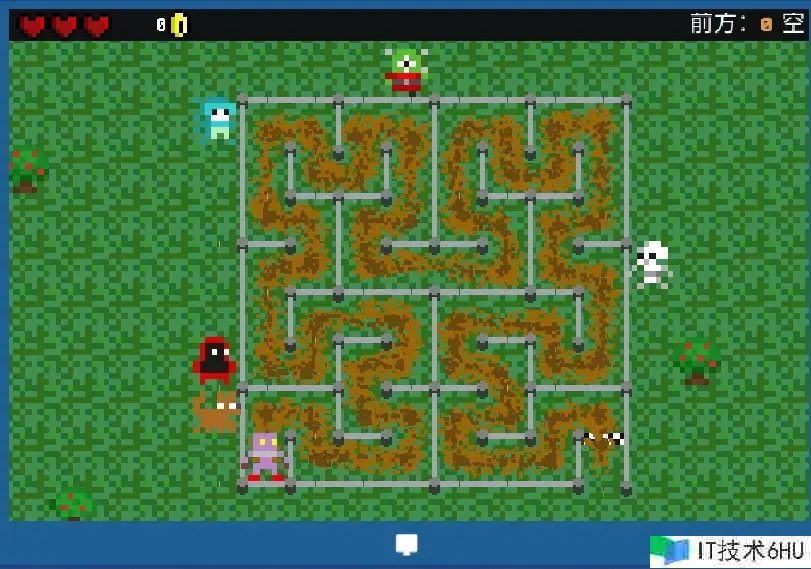
最近在玩 图灵齐备(Turing Complete) 一路过关斩将，来到 机器赛跑(Robot Racing) 这一关的时分，一看地图

关于选修过火形几许的我来说，这不便是了解的希尔伯特曲线嘛！老朋友了！于是我复活现已死去的和分形几许有关的记忆，用分形的思维初步完结了对应的汇编代码并经过了这一关。合理我自鸣得意并在网上检查其他人处理这一关的思路的时分，我看到了这一篇文章: 图灵齐备(Turing Complete)机器赛跑(Robot Racing)关卡纯汇编60字节达到成果留念，我才知道本来有个成果是要求汇编代码在 64 个字节内过关，而且这篇文章里用十分简练奇妙的办法达到了这个成果。

我和我弟弟一起探讨研究了这个办法的原理，现在咱们都了解了这个办法并直呼”Vocal！ “，文章里的办法实质上也是用到了分形的思维，但文章的作者只用了简略两句”简略发现，有显着的递归形式“和”注意到 r1、r2 可被兼并优化“，难倒一众英雄好汉，仿佛该作者一眼看透这个办法的实质，并觉得这十分简略无需多言(这便是大佬么.jpg)。然后我在这篇文章的启发下，也取得了“小机快跑”的成果。本文将用尽量通俗易懂的言语，为了解过和没了解过图灵齐备和分形的读者讲解用分形思维来经过机器赛跑这一关并达到成果“小机快跑”的思路，一起也将给出完结该思路的汇编代码。

图灵齐备

《图灵齐备》是一款电路模拟器游戏，于 2021 年在 Steam 上架。在这款游戏中，玩家可以从零开始构建计算机并编程它。在处理谜题的过程中，玩家将会学习到从基础逻辑门到算术单元、存储器等复杂元件的常识，并沿着这条道路终究学习怎么搭建完好的处理器架构。完结一切主线关卡后，玩家将对处理器架构、汇编言语和电子元件彼此之间的详细联络产生更加深刻的了解。玩家也会了解高档编程言语中常见的条件判别、循环、函数等概念是怎么在汇编和硬件层面详细完结的。 在本文中，读者无需重视电路细节，只需求重视算法中表现的分形的思维，以及怎么奇妙地简化算法即可。

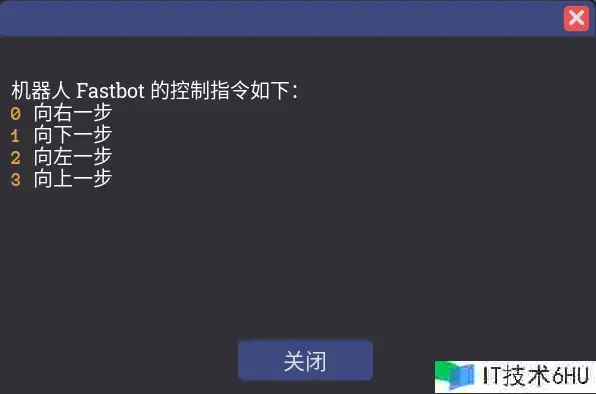
机器赛跑是最终一章汇编挑战里的一关，它要求玩家用汇编代码输出指令控制机器人移动走出迷宫，而“小机快跑”成果则要求玩家编写的汇编代码要尽或许简短， 只要今世码字节数不超越64才可取得该成果。

分形与希尔伯特曲线

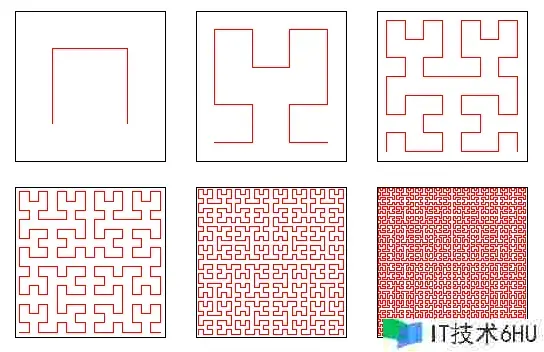
分形通常被界说为“一个粗糙或零碎的几许形状，可以分红数个部分，且每一部分都（至少近似地）是全体缩小后的形状¹”，即具有自类似的性质，例如最常见的雪花便是一种分形。而在机器赛跑这一关里，机器人地点的迷宫道路正好是分形几许里很经典的一种分形: 希尔伯特曲线。希尔伯特曲线一种能填充溢一个平面正方形的分形曲线（空间填充曲线），由大卫希尔伯特在1891年提出。称 $H_n$ 为一条希尔伯特曲线，假如 $H_n$ 满意以下性质:

$H_0$ 为正方形的中心点；
将 $H_n$ 等比例缩小到本来的 $14frac{1}{4}$ ，记为 $Hn′H^{prime}_n$ 。记 $Hn′H^{prime}_n$ 最靠近左下角的点为 $s_n$ ，最靠近右下角的点为 $t_n$ 。 $H_{n+1}$ 依照以下方法衔接生成:
1. 将正方形等分红 $22$ 个小正方形；
2. 令左下角的小正方形为顺时针旋转 $90$ 后的 $Hn′H^{prime}_n$ ；
3. 令左上方和右上方的小正方形为 $Hn′H^{prime}_n$ ；
4. 令右下方的小正方形为逆时针旋转 $90$ 后的 $Hn′H^{prime}_n$ ；
5. 衔接左下方的 $s_n$ 与左上方的 $s_n$ ；
6. 衔接左上方的 $t_n$ 与右上方的 $s_n$ ；
7. 衔接右上方的 $t_n$ 与右下方的 $t_n$ 。

可以严格证明， 当 $n \to \infty$ 时， $H_n$ 会在正方形中稠密，即会填满正方形平面。

假如将正方形等分红 $2n2n2^ntimes2^n$ 个小正方形，则简略看出， $H_n$ 具有以下性质:

$H_n$ 会经过一切小正方形的中心点，而且每个小正方形只会经过一次；
相邻的两个小正方形之间至多有一条连线；
不相邻的两个小正方形之间没有连线；
$H_n$ 为一条折线，两个端点别离位于最左下角和最右下角的小正方形中心点；
$H_n$ 是没有方向的；
$H_n$ 是左右对称的。

正文

有向希尔伯特曲线

虽然说迷宫的道路是希尔伯特曲线，但实际上是有一点区其他， $H_n$ 是没有方向的，但迷宫途径是有方向的，是要从左下角的起点走到右下角的结尾的。因而咱们需求模仿 $H_n$ 的界说，给出有方向的希尔伯特曲线的界说。

称 $Hnhat{H}_n$ 为一条有向希尔伯特曲线，假如 $Hnhat{H}_n$ 满意以下性质：

$H0hat{H}_0$ 为正方形的中心点；
将 $Hnhat{H}_n$ 等比例缩小到本来的 $14frac{1}{4}$ ，记为 $Hn′hat{H}^{prime}_n$ 。记 $Hn′hat{H}^{prime}_n$ 的起点为 $snhat{s}_n$ ，结尾为 $tnhat{t}_n$ 。 $Hn+1hat{H}_{n+1}$ 依照以下方法衔接生成:
1. 将正方形等分红 $22$ 个小正方形；
2. 令左下角的小正方形为途径回转并顺时针旋转 $90$ 后的 $Hn′hat{H}^{prime}_n$ ；
3. 令左上方和右上方的小正方形为 $Hn′hat{H}^{prime}_n$ ；
4. 令右下方的小正方形为途径回转并逆时针旋转 $90$ 后的 $Hn′hat{H}^{prime}_n$ ；
5. 衔接左下方的 $snhat{s}_n$ 与左上方的 $snhat{s}_n$ ，方向指向左上方的 $snhat{s}_n$ ；
6. 衔接左上方的 $tnhat{t}_n$ 与右上方的 $snhat{s}_n$ ，方向指向右上方的 $snhat{s}_n$ ；
7. 衔接右上方的 $tnhat{t}_n$ 与右下方的 $tnhat{t}_n$ ，方向指向右下方的 $tnhat{t}_n$ 。

这儿的途径回转指的是将途径从原本的起点走到结尾改为从结尾走到起点。而要进行途径回转的原因是，在拼接途径的时分，需求前一条途径的结尾走到后一条途径的起点，这样构成的才是一条新的途径，而假如不进行途径回转的话，会呈现“起点走到起点”或“结尾走到结尾”的状况，这样得到的就不是一个新的途径了。

假如将正方形等分红 $2n2n2^ntimes2^n$ 个小正方形，则简略看出， $Hnhat{H}_n$ 和 $H_n$ 有许多类似的性质:

$Hnhat{H}_n$ 从起点动身，会经过一切小正方形的中心点，而且每个小正方形只会经过一次，然后走到结尾；
相邻的两个小正方形之间至多有一条途径；
不相邻的两个小正方形之间没有途径；
$Hnhat{H}_n$ 的起点和结尾别离位于最左下角和最右下角的小正方形中心点；
$Hnhat{H}_n$ 是有方向的，从起点指向结尾；
$Hnhat{H}_n$ 进行途径回转等价于 $Hnhat{H}_n$ 进行左右镜像翻转。

其间性质6尤为重要，它是由 $H_n$ 的左右对称性决定的: 假如一条途径在疏忽方向的状况下是左右对称的，则这条途径进行途径回转等价于这条途径进行左右镜像翻转。而这个性质也意味着可以用更简便的办法来处理这个操作。

生成迷宫途径

简略看出，迷宫途径实际上便是 $H3hat{H}_3$ ，假如用给定的指令来表明途径的话， $H3hat{H}_3$ 是这样表明的:

为了更形象地表明途径，无妨记途径为指令 1 $\to$ 指令 2 $\to \dots \to$ 指令 $m$ ，例如 $1 \to 2 \to 3$ 。设 $h (n)$ 为 $Hnhat{H}_n$ 的途径表明，则由 $Hnhat{H}_n$ 的生成方法 2~7，咱们可以得到 $h (n)$ 的生成方法（这儿需求注意途径的先后顺序，以便利后边按顺序输出途径）:

$h (1) = 3 \to 0 \to 1$ ；
$h (n + 1) = f (h (n)) \to 3 \to h (n) \to 0 \to h (n) \to 1 \to g (h (n))$ ，

其间 $f$ 为将途径左右翻转后顺时针旋转 $90$ 的操作， $g$ 为将途径左右翻转后逆时针旋转 $90$ 的操作。而要给出对途径的全体操作的界说，实际上只需求给出对途径每一步的详细操作的界说即可。因而这儿只给出 $f$ 和 $g$ 针对每一步的详细界说：

\ 2, & x=1 \ 1, & x=2 \ 0, & x=3 end{cases} quad ,g(x)=begin{cases} 1, & x=0 \ 0,& x=1 \ 3, & x=2 \ 2, & x=3 end{cases} quad.

举例说明， $f (h (1)) = f (3 \to 0 \to 1) = 0 \to 3 \to 2$ ， $g (h (1)) = g (3 \to 0 \to 1) = 2 \to 1 \to 0$ 。于是关于任意给定的正整数 $n$ ，咱们都可以迭代生成对应的 $h (n)$ ，即不论希尔伯特迷宫有多少级，咱们都可以用一条公式给它秒了！

汇编代码完结及优化

在用代码完结之前，需求先简略了解一下什么是汇编言语。汇编言语是一种初级编程言语，用于与计算机硬件直接交互。它是计算机指令集架构的一种表现形式，运用符号代表计算机的机器指令。在汇编言语中，用助记符代替机器指令的操作码，用地址符号或标号代替指令或操作数的地址。汇编言语与计算机硬件的联系密切，每一条汇编句子都对应着底层的机器指令，直接操作计算机的寄存器和内存。

而《图灵齐备》很形象地展示了汇编言语是怎么操作寄存器和内存的，不过这不是本节的重点，本节只会摘取相关原理进行讲解。

语法

条件跳转操作码 参数 1  参数 2 跳转地址

意义

假如参数 1 和参数 2 依照条件跳转操作码对应的条件判别为真，则跳转到跳转地址对应的指令

比如

label test
// 其他代码
equl re0 re1 test

表明假如 re0==re1 则跳转到 test 对应的指令处，这儿 label 会将当时指令的地址赋值给 test

equl

语法

equl 参数1  参数2 跳转地址

意义

假如 参数1 == 参数2 则跳转到跳转地址对应的指令

比如

equl re0 re1 test

表明假如 re0==re1 则跳转到 test 对应的指令处

call

语法

call 函数地址 _ _

意义

调用函数，跳转到函数地址对应的指令

比如

label fun
# 其他代码
call fun 0 0

表明调用 fun 函数，跳转到 fun 对应的指令处

return

语法

return _ _ _

意义

跳转到上一次履行的 call 句子的下一句指令

比如

call fun 0 0
add re0 re1 re2
// 其他代码
label fun
// 其他代码
return 0 0 0

在履行 call 句子后会跳转到 fun 对应的指令处，当履行到 return 指令的时分，会跳转到上一次履行 call 句子的下一句指令，也便是 add 这一句

代码完结

本节的方针是以尽或许短的代码、尽或许少的寄存器数量和尽或许短的运转时刻来输出 $h (n)$ ，为此首要要对 $f$ 和 $g$ 进行处理。简略验证 $f (x) = (\sim x) &3$ ， $g (x) = x textasciicircum 1$ ，这儿要用到按位与“&”、按位取反“~”、按位异或“^“运算，均为简略的逻辑门运算，代码简略，运转速度快，而且” $&3$ “实质上便是对 4 取余，可以在不破坏值与指令一一对应联系的前提下将值限制在值的范围内。

下面给出的 Python 代码参阅了: 图灵齐备(Turing Complete)机器赛跑(Robot Racing)关卡纯汇编60字节达到成果留念:

n = 3
r0 = 0 # 第几层递归， h(r0) 为第 n-r0 层递归
r1 = 0 # 当时途径方向
def fill():
  global r0, r1
  if r0 is not n:
    r0 += 1
    r1 = ~r1 # f
    fill() # f(h(n))
    print(r1 & 3, end='') # 关于当时层 n 的指令 3
    r1 = ~r1 # 回溯
    fill() # h(n)
    print(r1 & 3, end='') # 关于当时层 n 的指令 0
    fill() # h(n)
    r1 ^= 1 #g
    print(r1 & 3, end='') # 关于当时层 n 的指令 1
    fill() # g(h(n))
    r1 ^= 1 # 回溯
    r0 -= 1 # 回溯
fill()

fill() 完结的功用是输出以 r1 为起点朝向的 h(n-r0)，而且从结尾出来后机器人的朝向仍为 r1。注意到 $f (f (x)) = x, g (g (x)) = x$ ，因而递归的回溯只需求再调用一次 $f$ 或 $g$ 即可。

将其翻译为汇编言语如下:

label fill
equl|imme2 re0 3 end
add|imme2 re0 1 re0
not|imme2 re1 0 re1 
call fill 0 0
and|imme2 re1 3 out
not|imme2 re1 0 re1
call fill 0 0
and|imme2 re1 3 out 
call fill 0 0
xor|imme2 re1 1 re1 
and|imme2 re1 3 out
call fill 0 0
xor|imme2 re1 1 re1
sub|imme2 re0 1 re0
label end
return 0 0 0

只需求 60 个字节，达到成果”小机快跑“！而且只用到两个寄存器，而且运转时刻也很短，十分高雅~

结语

汇编作为较底层的编程言语，其直接操作内存的方法赋予了这门言语共同的魅力。在优化 $f$ 和 $g$ 的过程中，我发现缺乏必定的 ”汇编直觉“ 或 ”逻辑门直觉’“是很难一眼看出优化方案的。一开始，我采用了较为笨拙的办法来完结这两个映射，直到阅读了那篇”简略看出“的文章后，我才豁然开朗，本来还能以这样的方法操作！

与此一起，分形是一门令人入神的学科，其美丽和奇妙之处让人为之倾倒。经过这篇文章，我希望可以激起更多人发现这枚数学珍宝的美丽。一起，我也鼓舞图灵齐备的玩家们努力完结 ”小机快跑“ 的成果！

参阅文献

Mandelbrot Benoit B. 1983. The Fractal Geometry of Nature. [New edition] ed. New York: Freeman. ↩

使用分形思想，通过图灵完备的机器赛跑关卡，并获得小机快跑成就

前语

图灵齐备

分形与希尔伯特曲线

正文

有向希尔伯特曲线

生成迷宫途径

汇编代码完结及优化

位和字节

寄存器

指令

add

语法

意义

比如

imme1

语法

意义

比如

imme2

语法

意义

比如

sub

语法

意义

比如

and

语法

意义

比如

xor

语法

意义

比如

not

语法

意义

比如

条件跳转

语法

意义

比如

equl

语法

意义

比如

call

语法

意义

比如

return

语法

意义

比如

代码完结

结语

参阅文献

Footnotes

相关文章

浅更一篇模拟登录

GPT-4、文心一言、AI作画 | 人工智能周刊第11期

基于websocket如何实现接口订阅，使用这个sdk就完事了

一文深入支付系统订单重试的最佳实践

作者信息