阿里（淘天）一面笔试算法原题

阿里撤资 “车来了”

近日，国内实时公交产品”车来了”相关公司武汉元光科技有限公司发生工商变更，阿里巴巴（我国）网络技术有限公司退出股东行列。

这很好理解，符合近期阿里收缩战线的行为一致性。

究竟自己一手打造的”饿了么”都被数次传出「摆上货架」的消息。

那些被阿里出资的项目，自然更是首战之地。

但阿里这个等级的公司，简略形成领头羊效应，成为引发雪崩的第一个初始雪球。

那些前期被阿里领投，现如今或许不是自身事务问题，但却遭遇阿里撤资的项目，失掉的或许并不只是阿里的出资，大概率还会包括那些前期跟随大公司步伐进行跟投的资金。

一个企业现在没有安稳的盈利事务（仅政企 + 广告），或许还是靠融资活着，假如原计划的资金超过 30% 不能及时到位，意味着资金链断裂，公司只能是面临裁人，乃至破产倒闭。

考虑到”车来了”是轻资产类型的公司，因而大胆估计近期会发生裁人，再撑一段时刻。

后续假如没有特别变化的话，比较好的出路应该会被其他互联网巨头收买，作为位置比地图低两个层次的基础设施而存在。

但说句很残暴的话，假如真的沦落到被收买，大概率会被贱卖，现在比较好的潜在卖家腾讯、百度、字节。

…

回归主线，来一道读者投稿的「阿里」一面算法原题。

读者反馈，阿里的题面并不如此，但意思和解法完全一致，属于换皮原题。

标题描绘

平台：LeetCode

题号：1457

给你一棵二叉树，每个节点的值为 1 到 9 。

咱们称二叉树中的一条途径是 「伪回文」的，当它满足：途径经过的一切节点值的摆放中，存在一个回文序列。

请你返回从根到叶子节点的一切途径中伪回文途径的数目。

示例 1：

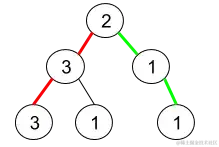
输入：root = [2,3,1,3,1,null,1]
输出：2 
解说：上图为给定的二叉树。总共有 3 条从根到叶子的途径：赤色途径 [2,3,3] ，绿色途径 [2,1,1] 和途径 [2,3,1] 。
     在这些途径中，只要赤色和绿色的途径是伪回文途径，由于赤色途径 [2,3,3] 存在回文摆放 [3,2,3] ，绿色途径 [2,1,1] 存在回文摆放 [1,2,1] 。

示例 2：

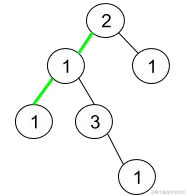
输入：root = [2,1,1,1,3,null,null,null,null,null,1]
输出：1 
解说：上图为给定二叉树。总共有 3 条从根到叶子的途径：绿色途径 [2,1,1] ，途径 [2,1,3,1] 和途径 [2,1] 。
     这些途径中只要绿色途径是伪回文途径，由于 [2,1,1] 存在回文摆放 [1,2,1] 。

示例 3：

输入：root = [9]
输出：1

提示：

• 给定二叉树的节点数目在范围 [1,105][1, 10^5][1,105] 内
• $1<=Node.val<=9$

DFS + 位运算

“伪回文”是指可以经过重新摆放变成“真回文”，真实的回文串只要两种状况：

• 长度为偶数，即呈现次数为奇数的字符个数为 $0$ 个
• 长度为奇数，即呈现次数为奇数的字符个数为 $1$ 个（位于中心）

因而，咱们只关怀途径中各个字符（数字 0-9）呈现次数的奇偶性，若途径中一切字符呈现次数均为偶数，或仅有一个字符呈现次数为奇数，那么该途径满足要求。

节点值范围为 $[1,9]$，除了运用固定大小的数组进行词频计算以外，还可以运用一个 int 类型的变量 cnt 来计算各数值的呈现次数奇偶性：若 $cnt$ 的第 $k$ 位为 $1$，阐明数值 $k$ 的呈现次数为奇数，不然阐明数值 $k$ 呈现次数为偶数或没呈现过，两者是等价的。

例如 cnt=(0001010)2cnt = (0001010)_2cnt=(0001010)2​ 代表数值 $1$ 和数值 $3$ 呈现次数为奇数次，其余数值没呈现过或呈现次数为偶数次。

翻转一个二进制数字中的某一位可运用「异或」操作，具体操作位 cnt ^= 1 << k。

判别是否最多只要一个字符呈现奇数次的操作，也就是判别一个二进制数字是为全为 $0$ 或仅有一位 $1$，可配合 lowbit 来做，若 cnt 与 lowbit(cnt) = cnt & -cnt 持平，阐明满足要求。

考虑到对 lowbit(x) = x & -x 不熟悉的同学，这儿再做简略介绍：lowbit(x) 表示 x 的二进制表示中最低位的 $1$ 地点的位置对应的值，即仅保存从最低位起的第一个 $1$，其余位均以 $0$ 填充：

• x = 6，其二进制表示为 (110)2(110)_2(110)2​，那么 lowbit(6)=(010)2=2lowbit(6) = (010)_2 = 2lowbit(6)=(010)2​=2
• x = 12，其二进制表示为 (1100)2(1100)_2(1100)2​，那么 lowbit(12)=(100)2=4lowbit(12) = (100)_2 = 4lowbit(12)=(100)2​=4

Java 代码：

class Solution {
    int ans = 0;
    public int pseudoPalindromicPaths (TreeNode root) {
        dfs(root, 0);
        return ans;
    }
    void dfs(TreeNode root, int cnt) {
        if (root.left == null && root.right == null) {
            cnt ^= 1 << root.val;
            if (cnt == (cnt & -cnt)) ans++;
            return ;
        }
        if (root.left != null) dfs(root.left, cnt ^ (1 << root.val));
        if (root.right != null) dfs(root.right, cnt ^ (1 << root.val));
    }
}

C++ 代码：

class Solution {
public:
    int ans;
    int pseudoPalindromicPaths(TreeNode* root) {
        dfs(root, 0);
        return ans;
    }
    void dfs(TreeNode* root, int cnt) {
        if (!root->left && !root->right) {
            cnt ^= 1 << root->val;
            if (cnt == (cnt & -cnt)) ans++;
            return;
        }
        if (root->left) dfs(root->left, cnt ^ (1 << root->val));
        if (root->right) dfs(root->right, cnt ^ (1 << root->val));
    }
};

Python 代码：

class Solution:
    def pseudoPalindromicPaths (self, root: Optional[TreeNode]) -> int:
        ans = 0
        def dfs(root, cnt):
            nonlocal ans
            if not root.left and not root.right:
                cnt ^= 1 << root.val
                ans += 1 if cnt == (cnt & -cnt) else 0
                return 
            if root.left:
                dfs(root.left, cnt ^ (1 << root.val))
            if root.right:
                dfs(root.right, cnt ^ (1 << root.val))
        dfs(root, 0)
        return ans

TypeScript 代码：

function pseudoPalindromicPaths (root: TreeNode | null): number {
    let ans = 0;
    const dfs = function (root: TreeNode, cnt: number): void {
        if (root.left == null && root.right == null) {
            cnt ^= 1 << root.val;
            if (cnt == (cnt & -cnt)) ans++;
            return ;
        }
        if (root.left) dfs(root.left, cnt ^ (1 << root.val));
        if (root.right) dfs(root.right, cnt ^ (1 << root.val));
    }
    dfs(root, 0);
    return ans;
};

• 时刻复杂度：$O(n)$
• 空间复杂度：$O(\log n)$

我是宫水三叶，每天都会共享算法题解，并和我们聊聊近期的所见所闻。

欢迎重视，明天见。

更多更全更抢手的「书面考试/面试」相关资料可访问排版精巧的 合集新基地