Part 1:监督学习
在提到机器学习的时分,往往咱们说的是一类算法,这些算法让机器能够模仿出人的行为,去进行一些有含义的操作。简略的来讲,咱们能够让它判别,面前这张照片中的小动物是猫仍是狗,从患者的CT照片中判别患者是否有潜在的病灶,或许,判别一块数据中是否包括有恶意的代码,等等。
而当咱们描述某一种机器学习算法,或许说,当咱们给无数机器学习算法进行分类时,咱们能够大致上将其分为两类,即:监督学习与无监督学习。这一篇文章,咱们将对监督学习打开讨论。
Part 2:监督学习的结构与原理
让咱们先列举几个简略且经典的机器学习问题——
- 对动物或植物的种类进行判别
- 对手写的数字或字符进行辨认
- 对患者是否患有某种病症进行辨认
机器学习是一个学习的进程,为了让机器能够做出正确的判别,并处理上面的问题,咱们首要需求为机器学习算法的“模型”供给用于学习的数据。在这里,以及鄙人文中,咱们将那个经过机器学习算法构建的,用于处理某个具体机器学习问题的“事物”称为机器学习“模型”。不要由于第一次传闻这个词而感到茫然,本质上来说,它是一个能够继续对数据进行处理,并履行咱们期望他完成的使命的程序(也便是咱们敲代码敲出来的文件)。
接下来,咱们对上面列出的“种类判别”问题进行打开。在机器学习的研讨中,有一个很经典的,现已被绝大多数书籍和课程作为机器学习入门事例的问题是“鸢尾花问题”[1]。一位叫做安德森的美国植物学家曾收集了150份鸢尾花的样本,这些样本来源于鸢尾花的三个亚属,分别是山鸢尾,变色鸢尾和维吉尼亚鸢尾,每个样本都被测量了花萼和花瓣的长度和宽度。在鸢尾花问题中,咱们运用这些特征去区分不同的亚属。
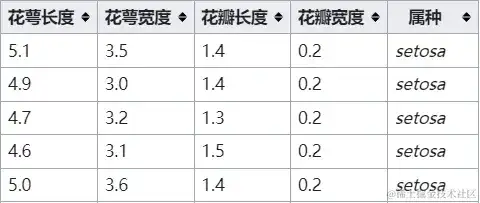
Fig 2.1 安德森鸢尾花数据集的部分内容
观察一下这份数据集的结构,咱们不难看出,同一份样本的花萼,花瓣的长宽,被放入了数据库的同一行中,每一行的最终,则标明晰该样本的属种。咱们用前四个特点,能够找到这份数据库中的一个仅有样本,而第五个特点“属种”,则是咱们需求模型帮咱们判别的“种类类别”。
在监督学习中,咱们供给给模型进行学习的数据,就这么被咱们称为样本和标签,即 sample 和 label。
咱们在此要先强调一个客观事实:即使同为鸢尾花,这三个属种仍然有较为普遍的差异。举另一个例子来说明这一点,雪纳瑞作为一个犬种,其三个细分种类,大型雪纳瑞,规范雪纳瑞和迷你雪纳瑞,彼此在体型上都有较为显着的差异。最小的规范雪纳瑞,可能与最大的迷你雪纳瑞在体型上接近,但一定会显着的比大多数迷你雪纳瑞要更大些,鸢尾花同理。
当这一份数据库被送给模型时,模型会准确的记载这150个样本的全部数据,以及他们的标签。这样一来,模型就对每个属种的鸢尾花有了一个根本的认知,未来,当咱们把一个不知道属种的鸢尾花给到模型时,模型就会根据其对各属种已经产生的映像(过往各样本的准确数据),根据某些特定的规矩(在编写代码时制定的方法)猜想新的这朵鸢尾花归于什么属种。尽管猜想的成果不能确保肯定正确,但是在已经记载了很多样本的特征之后,模型做出的判别在绝大多数时分,往往都是靠谱的。
用比较专业的话来说,这是一个经过很多的数据来训练模型,以使模型能够泛化到新的、未见过的数据的进程。
Part 3:“最近邻”算法
既然咱们说,机器学习是经过很多数据来训练模型,使模型能够泛化到新的,未见过的数据,那么这里泛化的原理是什么?模型根据什么样的逻辑运用过往的数据,并对新的数据进行判别?
对于模型来说,为了处理这一系列问题,它会按照科学家/工程师预设好的一系列有序的指令来打开作业,这一系列有序的指令,便是支撑机器学习模型的机器学习算法。今天咱们要介绍的最近邻算法,便是一个最基础,也最经典的机器学习算法之一。
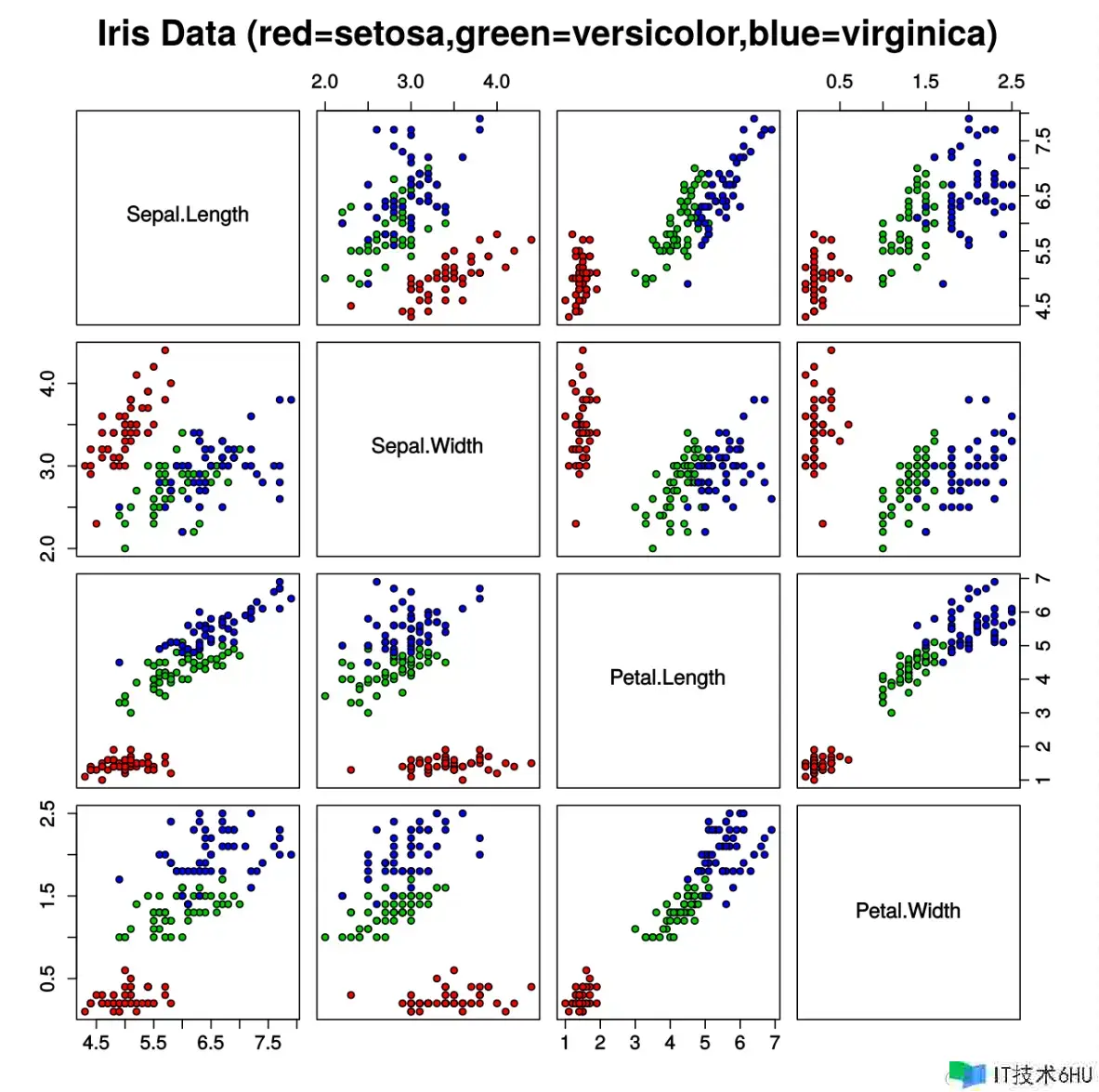
Fig 3.1 安德森鸢尾花数据集的散列图
上面这份四行四列的点图是安德森鸢尾花数据集的散列图,它的每一个子图中都有150个点,分别对应数据会集的每一个样本,不同类型的样本被用不同的色彩表示,而这些子图的横纵坐标,则是咱们收集的样本的四个特征的任意两两组合,比方【花萼长,花萼宽】,【花萼长,花瓣长】,等等。
在这张图中咱们发现了一个风趣的现象,相同色彩的点往往会集在一同,并且在大多数时分,咱们能观察到不同色彩的点往往会集在不同的方位。形成这一现象的原因在于,同一个种类的鸢尾花,在各个特征上尽管会有细微的差异,但这份差异将显着小于其与不同种类的样本在相同特征上的差异。同时,换句话说,当咱们指定图中某一个点A时,咱们有理由相信,比起和它间隔较远的另一个点B,它更可能和与它间隔极近的点C是同一种类型。说的再简略一点,间隔较近的两个点,更有可能是同一种类的样本。
接受了这一客观现实后,咱们有理由相信,当不知道的第151份样本到来时,咱们只需求确认,现有数据会集,各项特征都与它最附近的样本(sample)是什么标签(label),它大概率也就会是什么标签。这便是“最近邻”算法的逻辑。
在真实的核算中,咱们经过欧几里得间隔衡量每个样本之间的间隔,及,求和两个点在各维度上间隔的肯定值的平方,再取成果的平方根,便是这两个点在空间中的间隔。
当然了,从图3.1中,咱们也发现在一部分子图上,代表versicolor的绿色点与代表virginica的蓝色点比起纠缠在了一同,与此同时,代表setosa的红色点在有些子图上能够观测到一个特别不合群的个体。在仅观测两个特征时,最近邻算法可能难以对其做出有效的判别,但是当咱们将四个特征调集在一同考虑时,更多特征之间的差异,将补偿某个特征带来的混杂。由此,咱们能够得出,当咱们运用最近邻算法时,尽可能多的统计不同的特征(尤其是这些特征在不同种类间差异较大时)将有效提高模型的性能。
除此之外,咱们也能够考虑统计,与待分类节点最近的三个节点,五个节点,而非一个节点的种类,取其间较多者作为对新样本的种类判别,这也是有效消除误差的办法。当咱们进行这种操作时,最近邻算法就变成了K近邻算法,其含义在于“根据离新样本最近的K个训练样本的标签”来判别新样本的标签。
鸢尾花数据集与最近邻算法常常在各教材中被当作入门事例进行讲解,具体的代码完成非常简略,在此不做打开。经过对这个算法的讲解,咱们能够对机器学习模型与算法有一个根本的认知。与其他一切的范畴相同,在机器学习方向,咱们也是经过一个流程化的步骤去处理一个问题,而更杂乱的机器学习模型与算法,也只是运用更杂乱的流程去更高效的处理数据罢了。
总结
本文旨在简略的介绍机器学习中的监督学习,与简略的最近邻算法,期望读者有理解了这两个知识点后,能够对“机器学习”有一个简略的认知,最根本的理解它的作业原理,让机器学习在读者眼里不再是一个“black box”一般的事物。
鄙人一篇文章中,我还会进一步的对监督学习进行一些补充,协助读者加深对监督学习的理解。
Reference
[1]安德森鸢尾花卉数据集zh.wikipedia.org/wiki/%E5%AE…