专栏的评价目标相关文章。

评价目标（一）| 精确率、精确率、召回率

书接上文，咱们已经讨论了精确率、精确率和召回率，本文将讨论 F1 分数 和 AUC 这两种常用目标。

1 F1分数

F1 分数是精确率和召回率的综合目标，它被界说为精确率和召回率的简略加权平均值（调和平均值），是统计学中用来衡量二分类模型精确度的一种目标。假如咱们用 $P$ 表明精确率，用 $R$ 表明召回率，那么 F1 分数能够表明为：

用 Python 完成如下。

def f1(y_true, y_pred):
    p = precision(y_true, y_pred)
    r = recall(y_true, y_pred)
    # 核算f1分数值
    score = 2 * p * r / (p + r)
    return score

In [X]: f1(l1, l2)
Out[X]: 0.5714285714285715

运转程序，咱们便能够得到该模型的 F1 分数。F1 分数的最大值是 $1$，最小值是 $0$，一般来说，越接近 $1$，说明模型的性能越好，能够更精确地猜测正例。

2 AUC

在学习 AUC 之前，咱们得先了解另外两个术语 TPR 和 FPR。

2.1 TPR

TPR 或称真阳性率（True Positive Rate），它与召回率相同，即表达式相同。它指的是一切实践为阳性的样本被正确地判别为阳性的个数与一切实践为阳性的样本个数之比。

因为TPR与召回率适当，所以它的 Python 完成很简略。

def tpr(y_true, y_pred):
    return recall(y_true, y_pred)

另外，TPR 或召回率也被称为灵敏度。

2.2 FPR

FPR 或称假阳性率（False Positive Rate），它的含义是一切实践为阴性的样本被错误地判别为阳性的个数与一切实践为阴性的样本个数之比。

FPR 的 Python 完成如下。

def fpr(y_true, y_pred):
    fp = false_positive(y_true, y_pred)
    tn = true_negative(y_true, y_pred)
    # 核算假阳性率
    return fp / (fp + tn)

2.3 ROC曲线和AUC

对于之前的讨论，咱们都是安身在一个猜测成果只为 $0$ 和 $1$ 的模型 $A$ 上。现在咱们要提出另外一个模型 $B$。假定咱们只有 $15$ 个样本，其标签值是二元的。同时，咱们练习了一个类似于随机森林的模型 $B$，并得到了样本呈正例的概率。

# 真实样本标签
y_true = [0, 0, 0, 0, 1, 0, 1,0, 0, 1, 0, 1, 0, 0, 1]
#猜测样本为正例（1）的概率
y_pred = [0.1, 0.3, 0.2, 0.6, 0.8, 0.05,
          0.9, 0.5, 0.3, 0.66, 0.3, 0.2,
          0.85, 0.15, 0.99]

为了评价该模型的精确率、召回率和 FPR 等数值，咱们需求挑选一定的阈值，有一个简略的办法就是选取 $\ge 0.5$ 的典型阈值。但事实上，咱们能够挑选从 $0$ 到 $1$ 之间的任何值作为阈值，以全面地评价模型。

# 猜测阈值
thresholds = [0, 0.1, 0.2, 0.3, 0.4, 0.5,
             0.6, 0.7, 0.8, 0.85, 0.9, 0.99, 1.0]

接下来，咱们核算该模型在不同阈值下的 TPR 和 FPR。

tpr_list = []
fpr_list = []
for thresh in thresholds:
    # 若样本为正例（1）的概率大于等于阈值，为1，否则为0
    temp_pred = [1 if x >= thresh else 0 for x in y_pred]
    temp_tpr = tpr(y_true, temp_pred)
    temp_fpr = fpr(y_true, temp_pred)
    tpr_list.append(temp_tpr)
    fpr_list.append(temp_fpr)

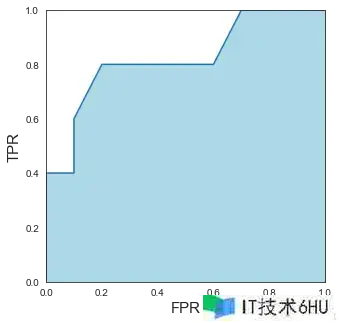
最终，咱们将 $tpr\_list$ 和 $fpr\_list$ 两个列表以散点图的形式绘制出来。

import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
plt.figure(figsize=(5, 5))
sns.set_style('white')
plt.plot(fpr_list, tpr_list)
plt.fill_between(fpr_list, tpr_list, color='lightblue')
plt.xlabel("FPR", size=15)
plt.ylabel("TPR", size=15)
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.0])
plt.show()

如图所示，这条从原点出发的曲线就是 ROC 曲线。假如咱们核算这条 ROC 曲线下的面积，即图中浅蓝色的多边形，就是在核算另一个目标——AUC。在这里咱们利用 scikit-learn 库现成的函数来核算 AUC 值。

In [X]: from sklearn import metrics
In [X]: metrics.roc_auc_score(y_true, y_pred)
Out[X]: 0.8300000000000001

运转程序，输出 AUC 值为 $0.83$。这是好还是坏呢？

AUC 是一种用于评价二分类模型性能的目标。它反映了模型在一切或许的阈值下的总体性能，较高的 AUC 值一般表明模型在区别正例和负例方面体现较好。AUC 的取值范围在 $0$ 到 $1$ 之间，$0.5$ 表明模型的性能与随机猜测相同，$1$ 则表明模型能够完美地将正例和负例区别开来，假如是 $0$ 的话则意味着这个模型非常糟糕。所以咱们练习的模型效果还算良好。

但 AUC 对咱们的模型有什么影响呢？

假定咱们方才树立的是一个从图片中检测气球的模型，其 AUC 值为 $0.83$，这意味着随机给定一张带有气球的图片（正样本）和一张不带有气球的图片（负样本），用咱们的模型进行分类和猜测，正样本的得分比负样本的得分要大的概率为 $0.83$。

现在，咱们已经具有了 ROC 曲线，那么怎么从中挑选出最适合这个模型的阈值呢？

根据从前给出的 TPR 和 FPR 的界说，咱们肯定是希望一个模型的 TPR 值较高，FPR 值较低，即模型能够辨认更多的正例，带来更少的误报。那么有一个常用的办法——等距最近点法，能够帮助咱们选出最合适的阈值。在这个办法中，咱们挑选 ROC 曲线上离左上角（即 FPR 为 $0$，TPR 为 $1$ 的点）最近的点对应的阈值作为最佳阈值。这种办法试图在真阳性率和假阳性率之间找到一个平衡，具体也能够经过核算每个点到左上角的欧氏间隔来完成，挑选间隔最小的点所对应的阈值。

import pandas as pd
data = {'threshold':thresholds, 'tpr':tpr_list, 'fpr':fpr_list}
df = pd.DataFrame(data)

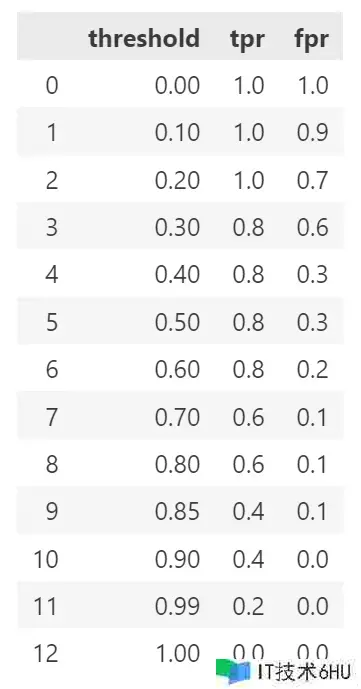
运转程序，得到成果如下。

简略核算一下，能够发现当阈值为 $0.6$ 时，模型 $B$ 的分类效果应该是最好的。

参考文献

F1分数

AUC

roc曲线最佳阈值

Approaching (Almost) Any Machine Learning Problem