前言
你有没有遇到过,某天报表的数据突显反常,排查后发现原来是单位弄错了。
你有没有遇到过,某组数据看起来没啥感觉,但做成报表组合到一同看问题则会十分显着。
你有没有遇到过,有些凭直觉来感受的计算信息与细心验算后的计算信息,终究得出的定论截然相反。
你有没有遇到过,某些根据计算结果得出的定论看起来没问题,但总觉得哪里不对劲。
我信任,只要你常看一些数据计算报表,或许会常做一些数据计算方面的工作,那你必定遇到过,大家常说数据不会哄人,但真的是这样吗?本篇文章首要就来揭秘一些既风趣、又能利诱人的常见手段。
中奖率1%,那是不是接连抽100次就必定会中奖呢?
幸存者误差
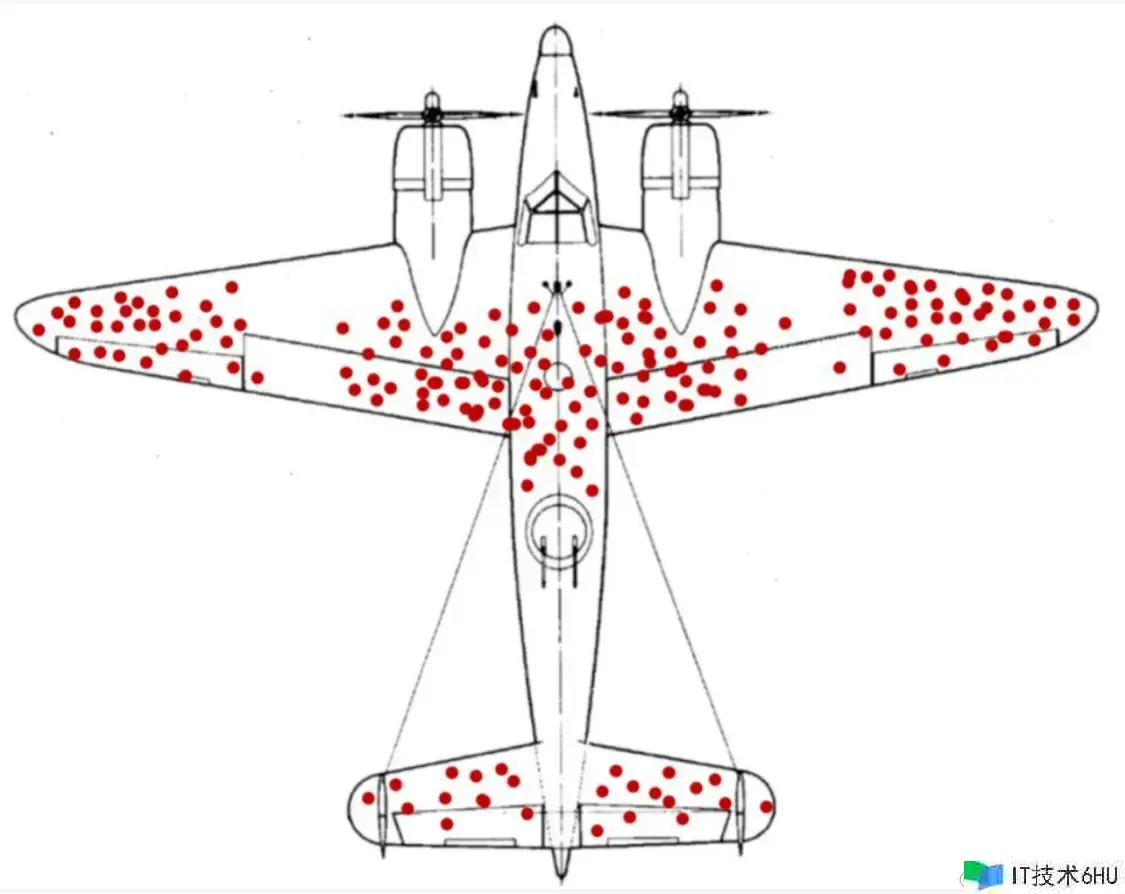
来自百度百科解说:1941年,第二次世界大战中,美国哥伦比亚大学计算学瓦尔德教授(Abraham Wald)应军方要求,使用其在计算方面的专业知识来供给关于《飞机应该怎样加强防护,才能下降被炮火击落的几率》的相关建议。沃德教授针对联军的轰炸机遭受进犯后回来营地的轰炸机数据,进行研讨后发现:机翼是最简略被击中的方位,机尾则是最少被击中的方位。沃德教授的定论是“咱们应该强化机尾的防护”,而军方指挥官认为“应该加强机翼的防护,由于这是最简略被击中的方位”。
日子中要特别留神由于忽视了幸存者误差而导致的问题,从前有人对兽医院接纳的从高层掉落的115只猫咪进行了查询,发现从9层及以上楼层掉落的猫咪的死亡率为5%,从不足9层的楼层掉落的猫咪死亡率为10%。所以估测,这是由于从较高楼层掉落的猫咪可以将身体伸展开,形成一种降落伞效应。显着,这个查询没有把那些从9层及以上掉落的已经奄奄一息没有被送到兽医院的猫咪考虑进来。
当然,还有一些查询计算,也会由于避开了幸存者误差,终究出具了一些看似比较美好计算结果。
美国运通和法国旅游局的一项研讨发现,大多数曩昔两年对法国进行过一次以上休闲旅游的美国人并不认为法国人不友好。他们究竟是怎样得到这个定论的呢?
一项简略的查询如下:
- 曩昔两年你对法国进行过几回商务游览?
- 曩昔两年你对法国进行过几回休闲(非商务)游览?
- 你是否认为法国人不友好?
从研讨人员得出的定论可以发现,他们将曩昔两年只去过一次的商务游览的人,或将曩昔两年只去过一次休闲游览的人,或从未去过法国的人,过滤掉了!
单从研讨的定论上来看它是正确的,但它却具有诈骗性,它存在幸存者误差。
有意思的反直觉场景
蒙提霍尔悖论
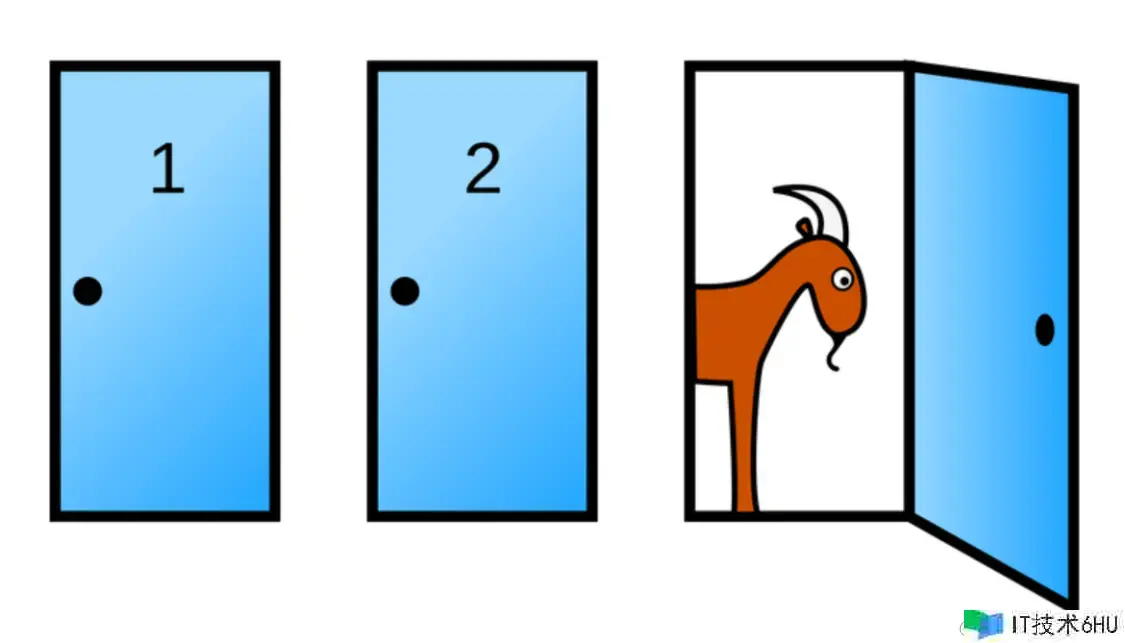
蒙提霍尔悖论又称三门问题,出自美国的电视游戏节目Let’s Make a Deal。问题的名字来自该节目的主持人蒙提霍尔(Monty Hall)。
这个游戏的玩法是:你被要求在三扇门中挑选一扇,其间一扇后边有一辆车;其余两扇后边则是山羊。你挑选了一道门,假定是一号门,然后知道门后边有什么的主持人,敞开了另一扇后边有山羊的门,假定是三号门。他然后问你:“你想挑选二号门吗?”
那么,转化你的挑选对你来说是一种优势吗?你会挑选换门,仍是坚持不变?
咱们可以分为下面三种状况进行剖析
三个囚犯问题
与蒙提霍尔悖论相似的还有三个囚犯问题。
问题是这样的:监狱里有三个死刑犯,假定分别为A、B、C,现在典狱长决议赦宥其间一名死刑犯,看守死刑犯的守卫知道赦宥的是谁,但他不能直接说。
假定A死刑犯问看守,他们三个之间谁会被履行死刑,看守只能依照下面三种状况来回答:
- 假如B被赦宥,看守就会说C被履行死刑了。
- 假如C被赦宥,看守就会说B被履行死刑了。
- 假如A自己被赦宥,看守就会在B和C中随机说一个被履行死刑了。
好了,假定现在看守人员告知A,B将被履行死刑,A监犯听了今后十分快乐,由于他觉得他被赦宥的概率一下从1/3提高到了1/2,而看守却告知他你被赦宥的概率仍然是1/3,快乐的应该是C,由于他被赦宥的概率提高到了2/3。
咱们仍然可以分为三种状况进行剖析

小心被图表诈骗
短少零值
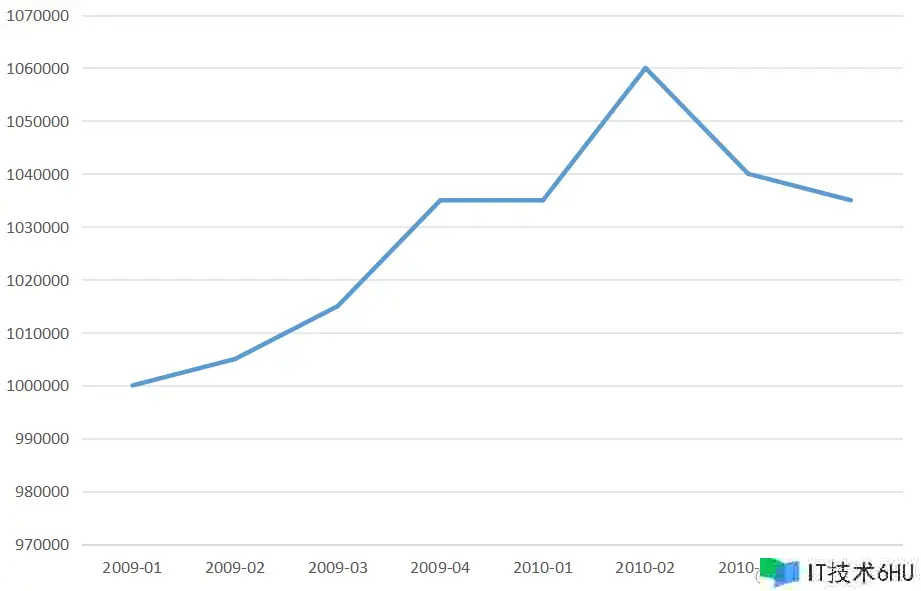
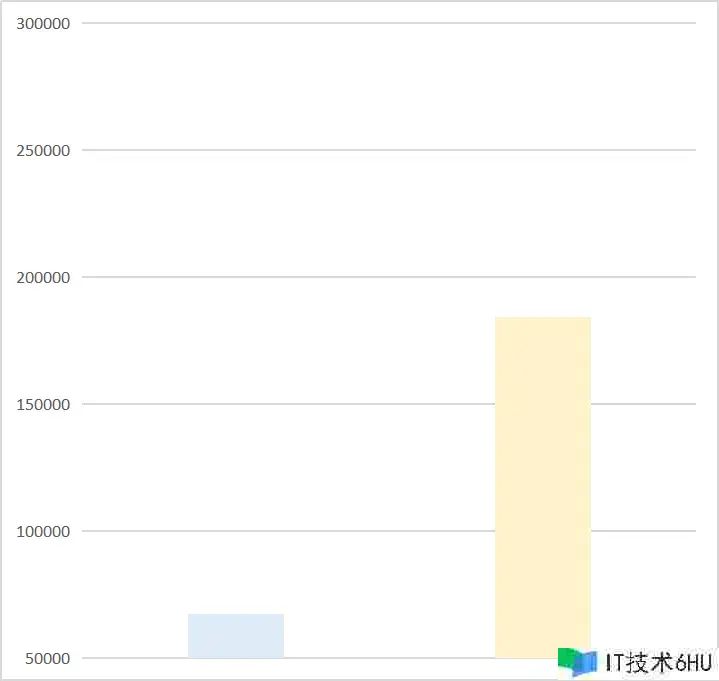
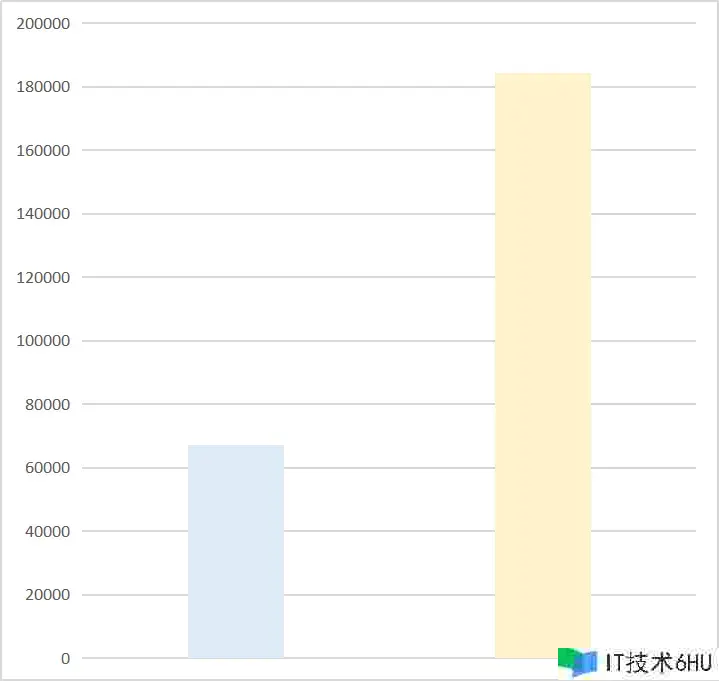
假如下面两张表分别表明了A公司B公司的销售额,或收入、开销等等之类的,你必定会觉得A改变比较大,而B公司比较稳定。但实际上下面两张表出自同一组数据,仅仅第一张表中短少了零值。
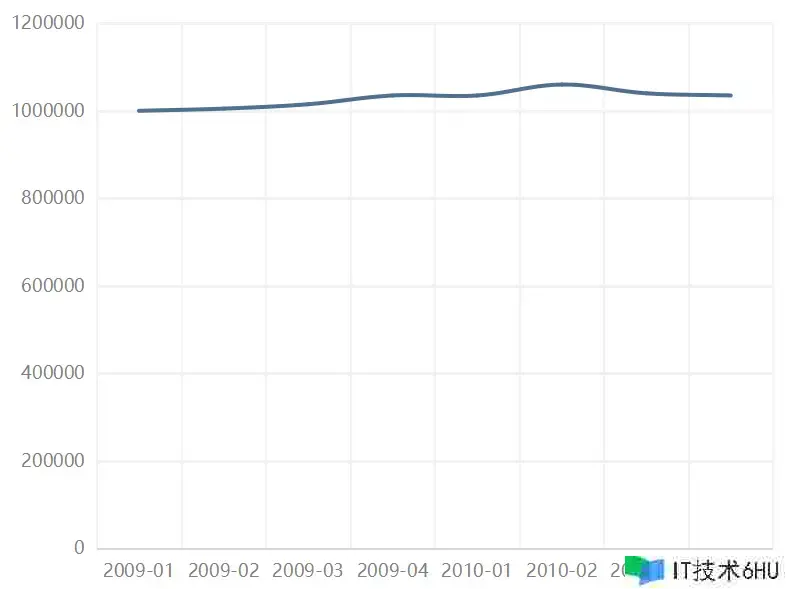
如下图,蓝色看起来显着要差很多,大约是5倍的关系。
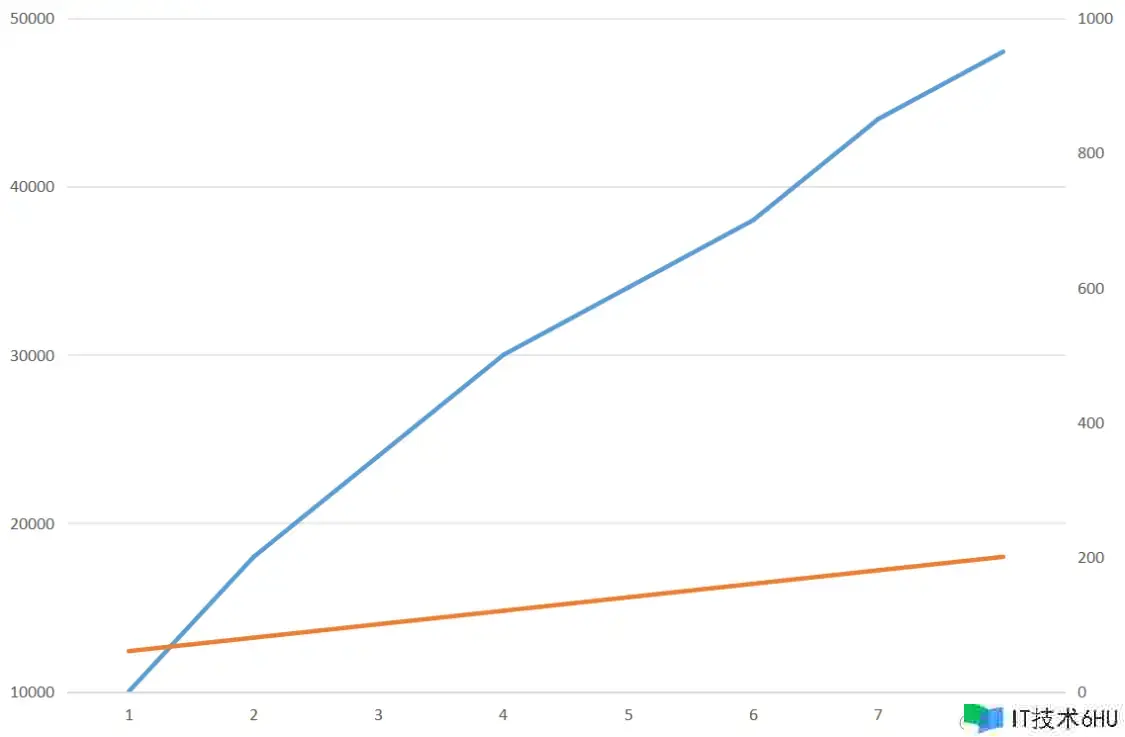
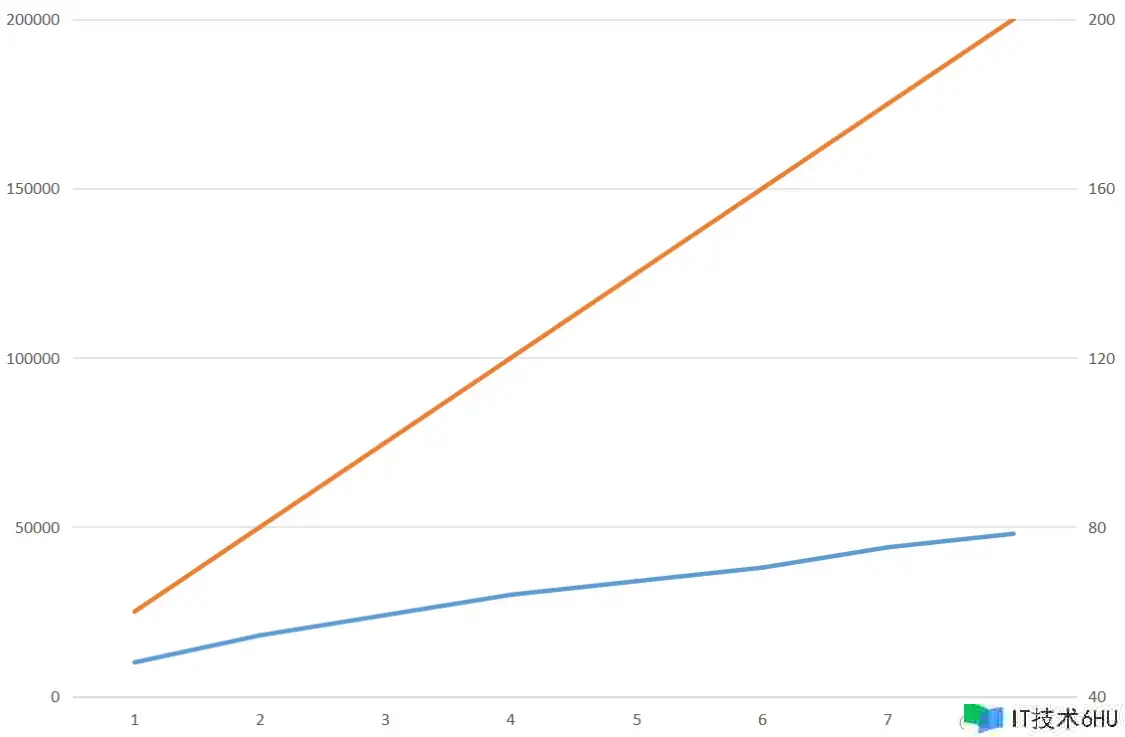
双坐标圈套
下面图表中,蓝线对应纵坐标左面的数值,橘线对应纵坐标右边的数值。
看起来蓝线的增加显着要高于橘线的增加。
现在呢!你还认为蓝线的增加高于橘线的增加吗?
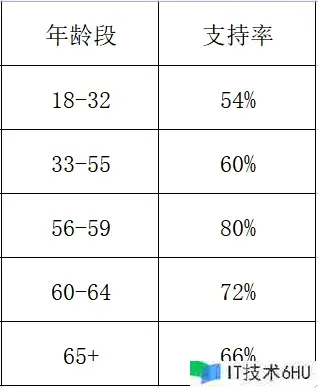
规模区间圈套
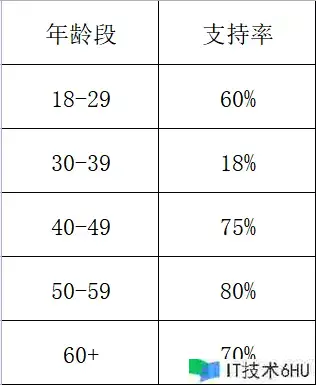
让支持率看起来愈加美丽
假如这样计算支持率看起来不太好看,30-39年龄段的支持率只要18%
左图是来自凤凰新闻,右图来自BBC。尽管两张地图都划了 5 个色块,但 BBC 将确诊病例大于 500 例的省份都赋予最严峻的深红色,导致了其时确诊 529 例的重庆和确诊 51986 例的湖北是一样的颜色,很有误导性。而凤凰网的数据划分规模就合理的多,是以 10 的次方为分界线。
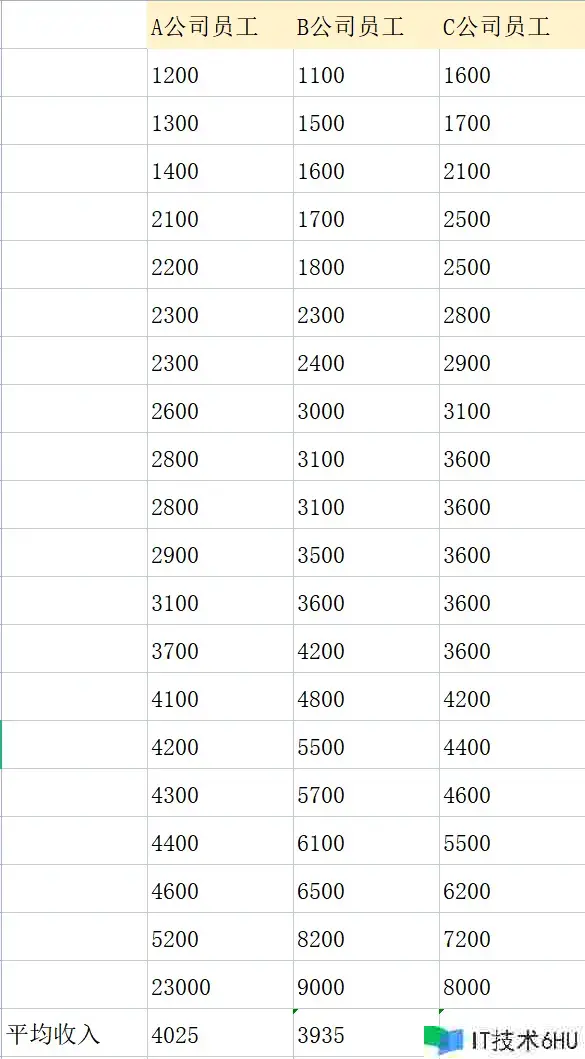
留神被平均值诈骗
假定下面是三家公司的每个职工工资收入报表。
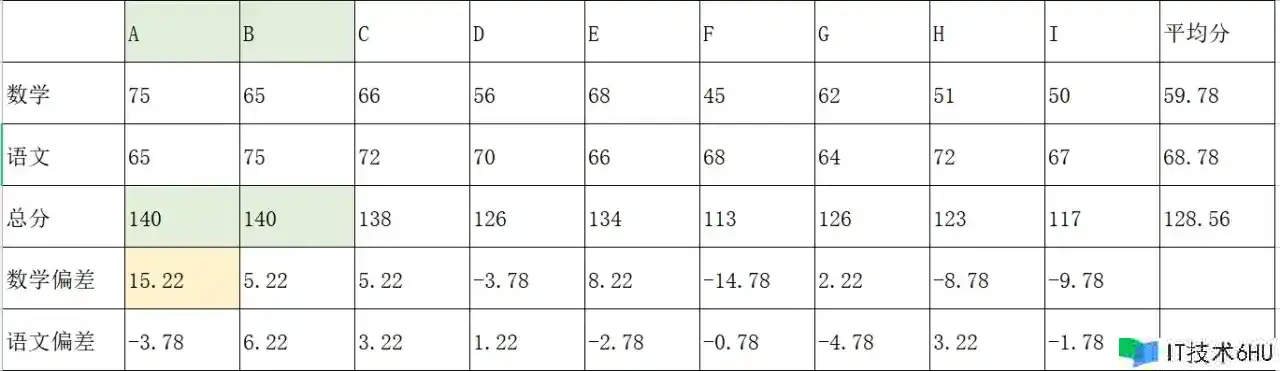
考虑误差
在下面这个考试成绩的报表中,尽管A和B的总分都是140分,但显着A的数学成绩是十分突出的(A的正误差值十分大)。
留神基数较小时
波士顿一份报纸报道说,韦尔弗利特当年的谋杀率是马萨诸塞州之最,每10万名居民中就有40起谋杀案,这个数字是波士顿的两倍多,后者每10万名居民中只要17起谋杀案。
这个计算是怎样来的呢?首先是有一名男子在30公里外犯下谋杀案,然后在韦尔弗利特警察局自首,但最关键的是韦尔弗利特只要2491名居民,再加上一项错误的计算,终究变成了每10万居民中就有40起谋杀。而波士顿发生了98起谋杀案,相当于每10万居民中有17起谋杀案。
所以将2491与100000放在一同进行比对,2491的动摇当然会比100000更大,尤其是反常数据带来的巨大影响。
相关性的误会
三段论推理是演绎推理中的一种简略推理判别,通过大前提、小前提、定论完成推理。亚里士多德提出的一个著名三段论:“所有的人都会死;苏格拉底是人;所以,苏格拉底必定会死。”
那么:“苏格拉底会死;动物也会死;所以,苏格拉底是动物。”
相似的问题,常常会体现在相关性的计算数据上。
美国的啤酒销量和已婚人口的数量,二者的相关性达到了惊人的99%。面临这种强烈的相关性,咱们可以认为饮酒会导致婚姻?或许倒过来,咱们可以认为婚姻会导致饮酒?
实际上,正确的解说是,跟着时刻的增加,啤酒消费量也会增加,相似的,婚姻、婴儿、轿车、鞋子、大学入学率、心脏病以及其他许多事物也会增加。穿鞋会导致婴儿数量增加吗?开车会导致心脏病吗?这些事物的增加源自人口的增加,它们之间不必定存在任何关系。
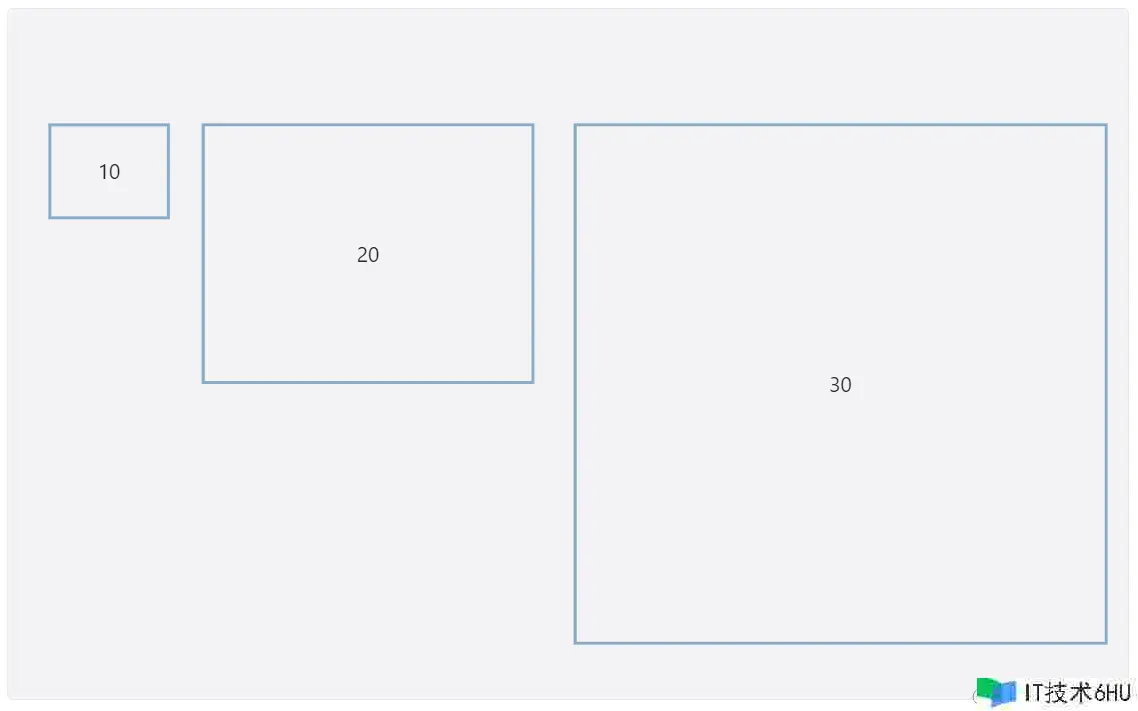
图形化诈骗
下面这张图想表达什么?20是10的2倍,30是10的3倍,但图中可不是依照这个份额来表明的。
真是的份额关系看上去应该是这样的