从零开始的数据结构Ep1-算法与复杂度

零、前言

欢迎拜访：

个人主页：conqueror712.github.io/

Github主页：github.com/Conqueror71…

笔者注：

本文，甚至本系列是我用于辅助自己学习的产物，难免会有些地方写的不如书本上那么精确，更多是关于常识结构的梳理以及自己的了解，毕竟不是要做一个“电子版的书本”，不会面面俱到。不过也请感兴趣的读者们定心，省略掉的重要内容，文中都会有标识，如今无论是搜索引擎仍是语言模型，想必都能够很快地处理疑问，感兴趣的话能够自行查找。

别的，我会将我自己梳理的常识结构图附上，以便大家能愈加一望而知地了解常识点之间存在的联系，在这其中或许会有一些了解不到位，或者过错的内容，烦请大家指出，这样一来也能更好地协助其他有需求的人。关于每章节的课后习题，我计划在有需求的时分做成视频讲解放在 Bilibili 上，供有需求的读者朋友们参阅。本文对应视频：✍️相关操练讲解视频

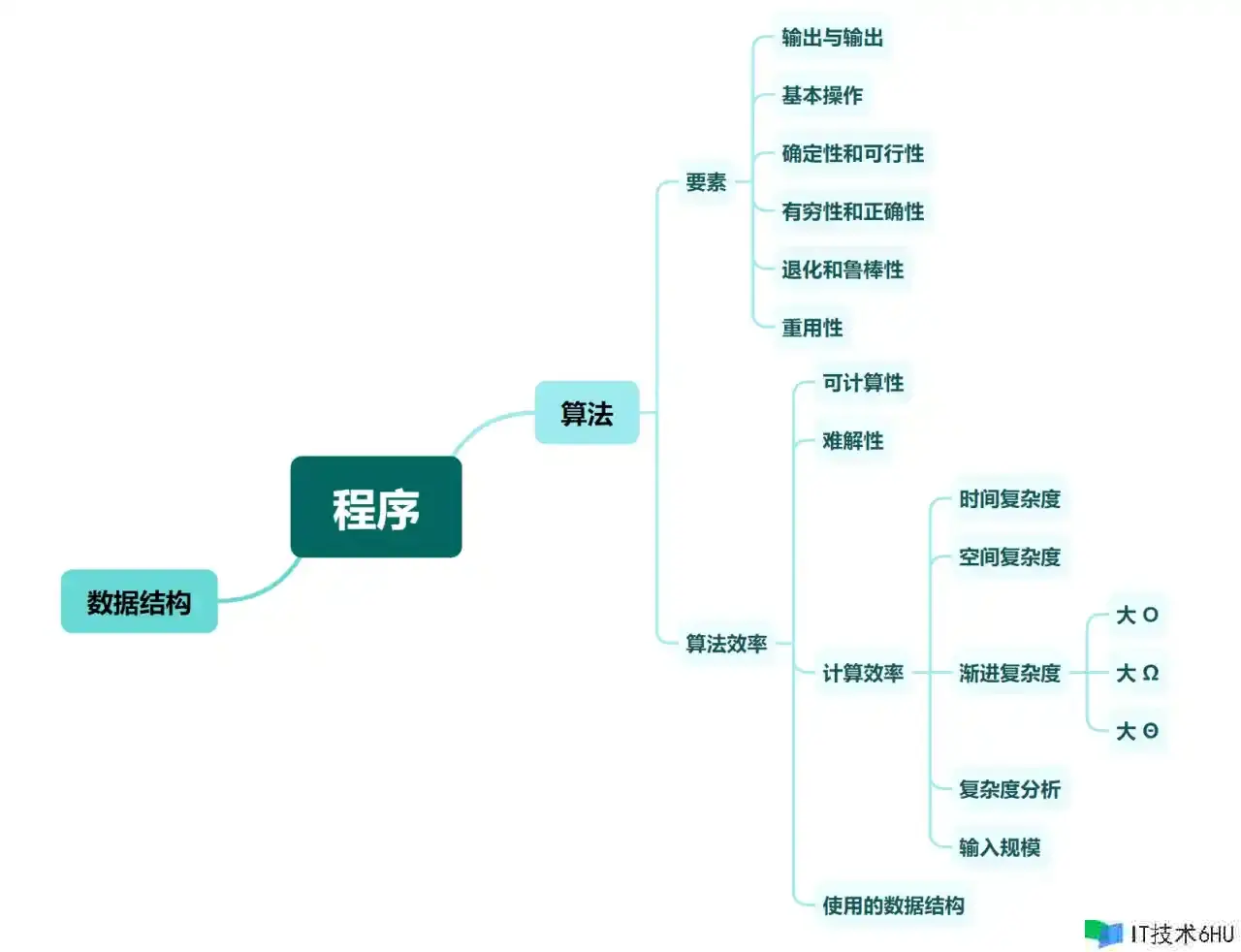
一、算法

已然咱们常说 DSA（Data Structure Algorithm = Program），那么，什么是算法？

• 是指基于特定的核算模型，旨在处理某一信息处理问题而规划的一个指令序列。

算法需求具有哪些要素？

• 输入与输出：不解说
• 根本操作：字面意思，不解说
• 确定性和可行性：算法应该能够被描述为由若干语义清晰的根本操作组成的指令序列，且每一根本操作在对应的核算模型中均可完成
• 有穷性和正确性：恣意算法都应在执行有限次根本操作之后停止，并给出能够符合给定问题下的正确输出
• 退化与鲁棒性：有用的算法应能够处理各种极端的输入实例，这里的极端情况便是所谓退化的情况，而算法为了能够尽或许充分地应对此类情况所具有的性质被称为鲁棒性
• 重用性：算法的整体框架能否快捷地推行至其他场合

算法功率触及哪几个方面呢？

• 可核算性：望文生义，例如无休无止的程序就不具有可核算性
• 难解性：有些算法虽然满意有穷性，但是实际上花费的时刻开支太大，这也属于难解性问题
• 核算功率：主要从时刻和空间这两个层面来衡量核算功率
• 数据结构：合理的数据结构能够协助规划出愈加优秀的程序

二、复杂度

• 时刻复杂度：

  从保存估量的视点出发，在规划为 n 的一切输入中选择执行时刻最长者作为 T(n)，并以 T(n) 衡量该算法的时刻复杂度

• 空间复杂度：

  与时刻复杂度类似地，算法所需存储空间的多少用空间复杂度来衡量，别的，时刻复杂度本身便是空间复杂度的一个天然的上界

• 渐进复杂度：

  渐进复杂度是渐进剖析的产物，这是一种着眼久远、更为重视时刻复杂度的整体改变趋势和增长速度的策略。为此，咱们将引进三种记号：

  • 大 O 记号：作为 T(n) 的渐进上界，详细界说如下：

    若存在常数 $c$ 及函数 $f(n)$，

    $s.t.$ 关于 $\forall n>>2$ 都有 $T(n)\le c\cdot f(n)$，（此处的 $>>$ 为远大于的意思）

    则可以为，在 $n$ 足够大之后，$f(n)$ 给出了 $T(n)$ 增长速度的一个渐进上界，

    此刻，记为 $T(n)=O(f(n))$

    别的还可得到两个性质：

    1. 忽略常数：关于 $\forall$ 常数 $c>0$，都有 $O(f(n))=O(c\cdot f(n))$
    2. 抓大头：关于 $\forall$ 常数 $a>b>0$，都有 O(na nb)=O(na)O(n^a n^b)=O(n^a)O(na nb)=O(na)

  • 大 记号：作为 T(n) 的渐进下届，详细界说如下：

    若存在常数 $c$ 及函数 $g(n)$，

    $s.t.$ 关于 $\forall n>>2$ 都有 $T(n)\ge c\cdot g(n)$，

    则可以为，在 $n$ 足够大之后，$g(n)$ 给出了 $T(n)$ 增长速度的一个渐进下界，

    此刻，记为 $T(n)=(g(n))$

  • 大 记号：作为 T(n) 的渐进确界，是对算法复杂度的精确估量——关于规划为 n 的任何输入，算法的运转时刻 T(n) 都与 (h(n)) 同阶，详细界说如下：

    若刚好 $f(n)=g(n)$，若存在正常数 c1<c2c_1<c_2c1​<c2​ 和函数 $h(n)$，

    $s.t.$ 关于 $\forall n>>2$ 都有 c1⋅h(n)≤T(n)≤c2⋅h(n)c_1h(n) ≤ T(n) ≤ c_2h(n)c1​⋅h(n)≤T(n)≤c2​⋅h(n)，

    则可以为，在 $n$ 足够大之后，$h(n)$ 给出了 $T(n)$ 增长速度的一个渐进确界，

    此刻，记为 $T(n)=(h(n))$

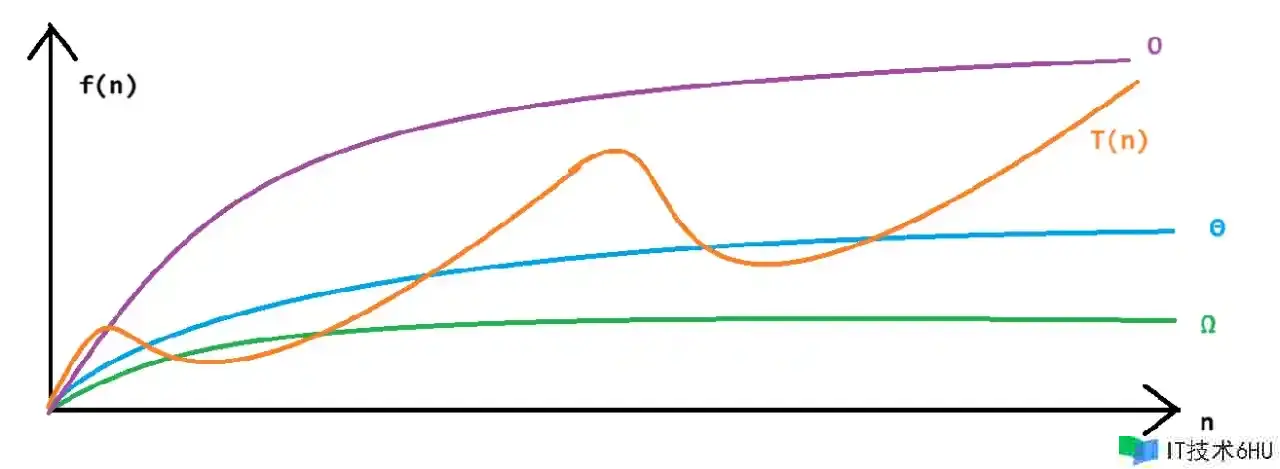
  咱们能够用一个图来直观的感受这三种记号之间的相关：

• 复杂度剖析：

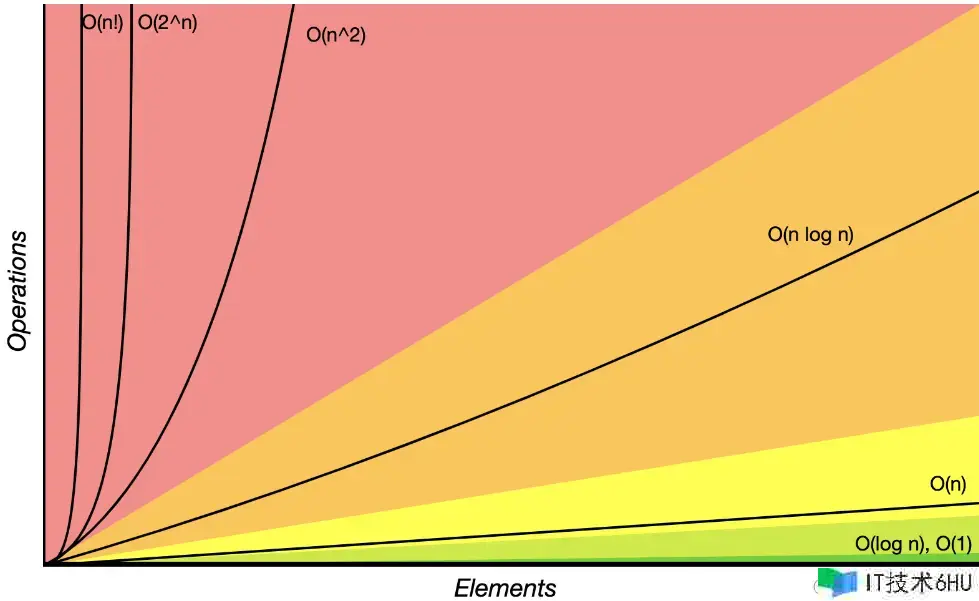
  典型的复杂度层次：

  • $O(1)$
  • $O(\log \log n)$
  • $O(\log n)$
  • O(n)O(sqrt{n})O(n​)
  • $O(n)$
  • $O(n\log \log n)$
  • $O(n\log n)$
  • O(n2)O(n^2)O(n2)
  • O(n3)O(n^3)O(n3)
  • O(2n)O(2^n)O(2n)

• 输入规划：

  严厉地说，所谓待核算问题的输入规划，应严厉界说为用以描述输入所需的空间规划。

  比方，若要计算恣意 n∈N n∈N_ n∈N ​ 的二进制打开中 $1$ 的个数，显然是经过遍历来计算的，一般咱们会默认用 $n$ 的巨细作为输入的规划，然后得到 $O(n)$ 的复杂度，但这是过错的，咱们称之为伪复杂度（本例中便是伪线性复杂度）。

  应当用 $n$ 的二进制打开的位数 r=1 ⌊log⁡2n⌋r=1 lfloor log_2nrfloorr=1 ⌊log2​n⌋ 作为输入的规划，然后得到正确的 $O(r)$ 复杂度。

弥补概念：数据调集及其对应的操作可超脱于详细的程序规划语言、详细的完成方式，即构成所谓的抽象数据类型（Abstract Data Type, ADT）。

✍️相关操练讲解视频

Question 1: 试证明，在用对数函数界定渐进复杂度时，常底数的取值无所谓。

证明：

设，某函数的上界能够表明为 f(n)=O(log⁡an),(a>1,a为常数)f(n)=O(log_an), (a>1, a 为常数)f(n)=O(loga​n),(a>1,a为常数)

则 f(n)=O(log⁡an)=O(ln⁡aln⁡n)=O(ln⁡bln⁡aln⁡nln⁡b)=O(ln⁡bln⁡alog⁡bn)=O(log⁡bn)f(n)=O(log_an)=O(frac{ln a}{ln n})=O(frac{ln b}{ln a}timesfrac{ln n}{ln b})=O(frac{ln b}{ln a}timeslog_bn)=O(log_bn)f(n)=O(loga​n)=O(lnnlna​)=O(lnalnb​lnblnn​)=O(lnalnb​logb​n)=O(logb​n)

即 O(log⁡an)=O(log⁡bn),O(log_an)=O(log_bn), O(loga​n)=O(logb​n),证毕

Question 2: 试证明，关于 $\forall >0$，都有 log⁡n=O(n)log n=O(n^)logn=O(n)。

证明：

直观地，咱们知道 $\ln x$ 的增长速度是慢于 $x$ 的

所以有 $\forall >0,\exists M>0s.t.n>M时,有\ln n<n$ ①

令 N=eM,N=e^M,N=eM, 当 $n>N,$ 即 $\ln n>M$（使用 $\ln x$ 的单调性）

总有 $\ln (\ln n)<(\ln n)$（使用 ① 式）

同时取 $e$ 为底数，得 eln⁡(ln⁡n)<eln⁡ne^{ln(ln n)}<e^{ln n}eln(lnn)<elnn，即 ln⁡n<nln n<n^lnn<n，则关于 $\forall >0$，log⁡n=O(n)log n=O(n^)logn=O(n)，证毕

Question 3: 若 f(n)=O(n2)且g(n)=O(n)f(n)=O(n^2)且g(n)=O(n)f(n)=O(n2)且g(n)=O(n)，试证明 f(n)g(n)=O(n3)f(n)times g(n)=O(n^3)f(n)g(n)=O(n3)

证明：

由大 O 记号界说得，

∃c1>0,N1>0,s.t.n>N1时总有f(n)<c1n2∃c_1>0, N_1>0, s.t. n>N_1时总有f(n)<c_1n^2∃c1​>0,N1​>0,s.t.n>N1​时总有f(n)<c1​n2

∃c2>0,N2>0,s.t.n>N2时总有g(n)<c2n∃c_2>0, N_2>0, s.t. n>N_2时总有g(n)<c_2n∃c2​>0,N2​>0,s.t.n>N2​时总有g(n)<c2​n

令 c=c1c2c=c_1c_2c=c1​c2​，N=max(N1,N2)N=max(N_1, N_2)N=max(N1​,N2​)

则当 $n>N$ 时，总有 f(n)g(n)<cn3=O(n3)f(n)times g(n)<cn^3=O(n^3)f(n)g(n)<cn3=O(n3)