GenAI的“关键一跃”：推理与知识

当时的人工智能范畴正通过生成式人工智能（GenAI）阅历一场严重改变。这一改变不只代表了技能上的腾跃，更标志着人工智能范畴的范式改变，引发了有关GenAI的共同特性及其深远影响的要害问题评论。

植根于核算革新的丰厚前史，本文从核算复杂性视点动身，探究推理和常识的实质，将前史性成就与最新的开展奇妙地交织在一起，以丰厚咱们对人工智能的了解。

（本文作者为吕坚平博士。以下内容经授权后由OneFlow编译发布，转载请联络授权。原文：
cplu.medium.com/reasoning-a…

作者 | 吕坚平

OneFlow编译

翻译｜宛子琳、杨婷

1

引言：核算革新的回响

GenAI象征着一个时刻，与核算机的前期年代相共识，这个年代以1931年库尔特哥德尔（Kurt Gdel）和1937年艾伦图灵（Alan Turing）的革新性奉献为标志。

他们的开创性作业开始旨在探究机器替代数学家的潜在或许，但无意中奠定了现代核算的根底。这种追求从头引发了人们对那个年代的一个重要问题的重视：“机器能否考虑？” 现在，这一问题现已演化为重视机器是否能像人类相同‘推理’和‘获取常识’，这是咱们现在所称之为通用人工智能（AGI）的要害特征。

回顾20世纪50年代艾伦图灵的有用办法，即通过实践看看效果怎么（let’s do it and see how it works）表现的哲学思想，GenAI的才能表现了这一精神。思想链（Chain-of-Thought（CoT））提示工程（prompting）（Wei, 2022）和检索增强生成（Retrieval-Augmented Generation（RAG））（Lewis, 2020）等技能展现了怎么让人工智能仿照人类推理和常识吸收办法，其要点是人机协同验证。思想链使人工智能能够在处理问题时“深思熟虑”，而RAG使得人工智能能够访问大量数据源以丰厚其回应。

比较之下，哥德尔对AGI的观念更为审慎、正确，他要点重视人类思想比较机器的优越性，在两者之间供给了一种必要的平衡。这种观念着重了在AI开发中选用理论上坚实和稳健的办法的重要性。风趣的是，当时人工智能范畴取得的开展，如新的练习办法和对齐战略，在某种程度上与哥德尔的准则是相照应的。

GenAI的演进还表现为使其能够自我参照和自我改善的先进技能，这些技能借鉴了哥德尔的数学洞悉力和图灵的核算理论。像Auto-CoT（Zhang，2022）和Self-RAG（Asai, 2023）等立异就是GenAI运用其技能进行自我增强的例子。

虽然GenAI的表现令人印象深化，但也面对着各种问题和应战，这些应战首要表现在扩展图灵遗产的经历主义办法上。从哥德尔的视点考虑这些应战，或许会为咱们供给宝贵的见地。这种情况呈现出一个明显的悖论：假如“P vs. NP问题”（核算复杂性范畴尚未处理的根本问题）得到明晰处理，或许会影响到哥德尔对人类思想优越性的观念。下文将详细讨论这一悖论及其对AGI的影响。

引言部分为深化讨论GenAI做了必定衬托。本文的方针是剖析GenAI怎么完成其杰出表现，并提醒其间固有的应战。咱们将专心于广泛的前史和办法论方面，这对GenAI的继续开展至关重要。

关于那些对核算的前史和理论根底感兴趣的人，推荐阅览“从不或许的机器到多功用核算机，再到AGI”部分。

对生成式人工智能的共同性以及它与核算机根底和图灵的经历主义办法的契合感到猎奇的读者，应深化了解“生成式人工智能是核算的全面扩展”部分。

要从哥德尔的视点了解推理和常识，“从第一性原理从头审视推理和常识”是阅览的首选部分。

终究，“从P vs. NP到AGI”部分将为读者供给对以人为中心的AGI的前瞻性见地。

2

从不或许的机器到多功用核算机，再到AGI

要充沛了解GenAI的革新性，就有必要深化探究艾伦图灵所想象的核算的根本问题。在图灵年代，由大卫希尔伯特（David Hilbert）领导的数学办法主义学派提倡一种观念，即一切数学常识都能够从一组根底正义或第一性原理中通过逻辑推导得出。这一年代见证了逻辑推理从亚里士多德年代有意识的思想练习开展为一种机械符号操纵体系。这种办法根植于逻辑规矩和数学正义的办法体系，标明数学家的聪明才智和固有的常识在数学中或许并非至关重要。这一思路还催生了通用证明机（universal proving machine）概念，该机器能够通过符号逻辑处理任何数学问题，而不依靠先前的数学常识——这是Entscheidungsproblem（断定问题）的中心概念。

从断定问题到停机问题

1931年，库尔特哥德尔的第一不齐备性定理从根本上改变了数学的面貌。该定理提醒了没有既能够“齐备（包括其规划内的每一条真理）”，又能够“共同（即没有对立）”的办法体系。哥德尔后来阐明晰其定理的深化含义，他说：“思想在运用中不是静态的，而是不断开展的，也就是说，随着咱们不断运用笼统术语，咱们对它们的了解会变得越来越精确。”（Copland，2013）。这着重了人类的参与在数学第一原理的了解和扩展中起着至关重要的效果，突显了只是从这些根本概念进行逻辑推理是不行的。

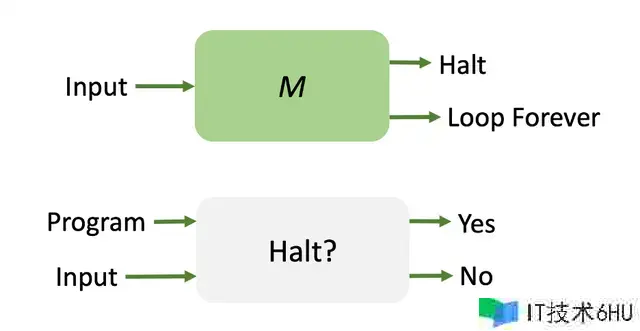
在这一改变的范式中，图灵走上了通向“断定问题”（Entscheidungsproblem）的另一条途径，偏离了对通用“证明”机的根究，转而研究通用核算机的或许性。其动机在于，这样一台机器将会过于强大以至于无法存在。它将能够自我参照，这必然会导致悖论。

这一探究的终究成果是图灵对停机问题的构想：在不实践运转某个机器的情况下，一台假定的机器，他称之为‘停机预言机（Halting Oracle）’是否能够确认任何给定的机器在特定输入下是否终究会停机，仍是会无限运转？图灵通过构思一个名为M的假定机器来应对这一应战，该机器被规划为直接违背停机预言机的猜测，如下图所示：

来历：作者

这导致了自指悖论（self-referential paradox）：

1. 假如M在给定M作为输入时停机，根据其界说，它将无限循环：这是一个对立。
2. 相反，假如M在输入M时无限循环，它应当停机：这是另一个对立。

来历：作者

这一深化的悖论使图灵得出一个重要定论：即停机预言机（一个想象中能够猜测任何机器运转成果的实体）是不或许存在的。因而，停机问题（即确认一个机器是否会停机或无限运转）成为了一个不行断定的问题。图灵的洞悉力进一步延伸到数学证明：假如存在一种通用的证明机制，理论上能够通过将每个数学问题从头表述为对预言的查询来将其转化为停机预言。因而，图灵对停机预言机不存在的证明间接地暗示了通用证明机制的不存在。反之，停机预言机的存在将答应创立一个通用证明机制，在这种机制中，证明（proof）被体系地搜索，然后咨询预言机该搜索是否会停机。因而，停机问题的不行解性与断定问题的不行解性有着内涵的联络，反之亦然。

现代核算的根底

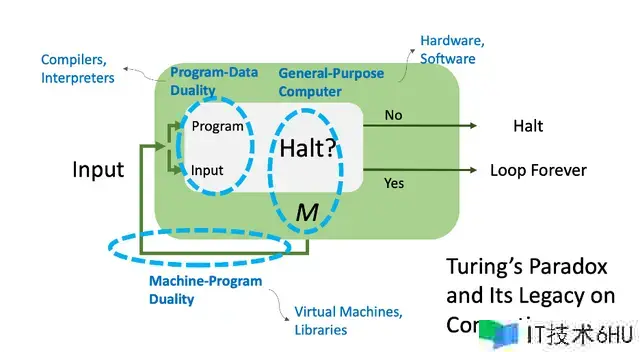
图灵的悖论的确对核算范畴发生了深远影响，并概括为如下三个刻画现代核算体系的界说性特征：

1. 通用核算机：图灵提出的一台能够仿照任何程序，乃至是停机预言的机器（M），它奠定了通用核算机的根底。这一立异明晰地区别了硬件和软件。
2. 机器-程序二元性：停机预言将M一起视为硬件和软件的概念引入了机器-程序二元性。这种二元性意味着程序能够被视为其他程序的硬件，比如虚拟机和库，然后构成不同层次的笼统。
3. 程序-数据二元性：图灵知道到M能够处理其他机器作为输入，这引发了程序-数据二元性的呈现。这一准则指出，程序能够被其他程序视为数据，使得编译器和解说器等软件东西得以完成。这种二元性是现代软件架构的中心。

缺乏通用的证明机制，或是理论上或许使软件工程变得过时的停机预言机，却意外地推动了核算机革新，催生了多功用的核算机和如今咱们所熟知的软件工程师所扮演的不行或缺的人物。

缺乏通用的证明机制或许停机预言机意外地推动了核算机革新，使得多功用核算机得以兴起，并刻画了软件工程师这一不行或缺的人物。

从人类直觉到通用人工智能

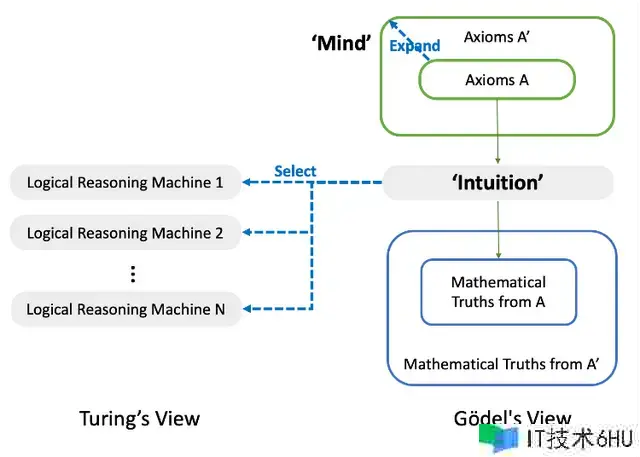
图灵的作业提醒了一个深化的悖论：办法体系内涵的逻辑推理的局限性有利于它们的机械化。这一知道突显了人类直觉的不行或缺性，特别是在从各种选项中“挑选”最适宜的定理证明机（theorem-proving machine）时，如附图所示。这种直觉进程相似于发现证明本身所触及的直觉。从现代核算的视点来看，挑选正确的机器就相似于编写程序，而图灵指出，程序员的直觉相似于数学家的直觉。

来历：作者

图灵的研究从头点燃了那个至关重要的问题：“机器能考虑吗？” 现在则改变为“直觉能被机械化吗？”。这种改变标志着关于通用人工智能（AGI）评论的深化演化，暗示AGI或许不只仅是核算革新的连续，而且或许是其巅峰。

要害问题，“机器能考虑吗？” 改变为 “直觉能被机械化吗？” 哥德尔的观念丰厚了这一概念，阐明晰人类思想在概念化和扩展正义方面的才能。这种才能能够通过从集合A过渡到A’的进程来展现，如图表所示。这种过渡逾越了机械化证明的范畴。他的这种见地着重了人类思想具有逾越机械化直觉束缚的共同才能。

3

生成式人工智能是核算的全面扩展

以言语大模型（LLM）为中心的生成式人工智能（GenAI）在通用意图的推理“硬件”方面开辟了一个充溢潜力但也充溢应战的世界。这场革新的中心是一种被描述为“不知而行（doing without knowing）”或许“通过实践看看效果怎么（let’s do it and see how it works）”的对立办法。这种办法表现为，GenAI依靠涌现才能而非明晰编程的特征，使其在各个范畴展现出杰出乃至“不合理”的效果。但是，支撑其习惯性的这一特征也会导致算术过错等根本过错，以及所谓的“错觉”现象。在这些情况下，GenAI自傲地发生引人误解或不精确的信息，突显出对其本身常识束缚的知道缺乏。GenAI内部的这种二重性——多功用以及简略出错的特征——令人着迷，引发了人们对其才能的热情，一起也需求慎重对待。

咱们对生成式人工智能（GenAI）的热情是对立的，因为它不只毫不费力地展现出巨大的潜力，又预示了一个充溢希望却又复杂的未来。它被以为是“不合理”的有用性，意味着GenAI表现出核算的实质特性，使其成为一股革新性的力气，相似于核算本身。

GenAI的有用性意味着它具有相似核算本身的实质特性。

LLM作为新硬件

深化讨论言语大模型的详细特性，咱们能够确认其间的三个要害特点：

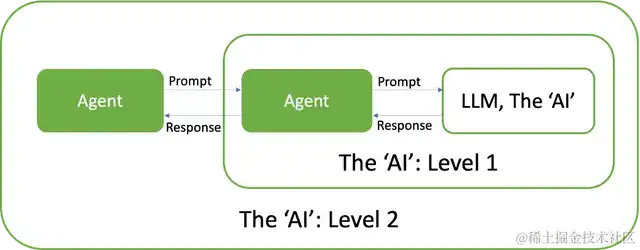
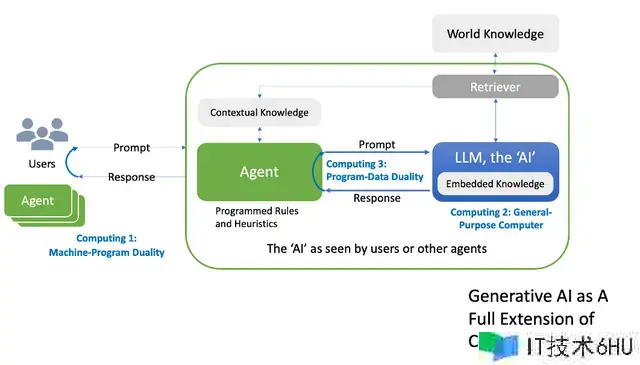
1. 天然言语接口：LLM擅长了解和生成人类言语，因而能够与其进行直观互动。这使得体系能够处理高档提示和呼应，包括“智能体（agent）”，即促进用户和LLM之间交互的软件模块。这种动态进程关于GenAI的“机器程序二元性”至关重要。在这种架构的每个笼统层级中，体系呈现出外部智能体或用户所感知的人工智能，这与现代核算体系中的多层次架构相照应。
2. 指令遵从：因为机器-程序二元性，LLM被视为人工智能笼统层次结构中的根底元素，十分擅长处理天然言语指令。这相似于核算机中CPU的功用，将LLM定位为一种通用推理“硬件”。它能了解广泛的指令和使命，使其在认知和推理使命范畴具有核算机硬件的多功用性。这一特性凸显了GenAI在各种运用中的功用，反映出通用核算机的习惯性。
3. 上下文学习/少样本学习：LLM的这一明显特点使其能够从有限的示例中学习和习惯，乃至能够从本身的输出中学习。这标明晰核算中固有的程序-数据二元性，即数据（在本例中是学习示例或生成的内容）能够被从头输入作为程序指令。这种在少量示例中继续学习和习惯的才能反映了数据和程序可互换的动态性质，这是核算的一个要害特征。

来历：作者

以革新性的视角来看，GenAI不只仅是核算的一个分支，更是其全面的延伸，预示着相似于图灵年代发起的核算革新的改变。这种对核算中心特征的整合表现在以下图表中：

来历：作者

生成式人工智能立异成为新的软件工程

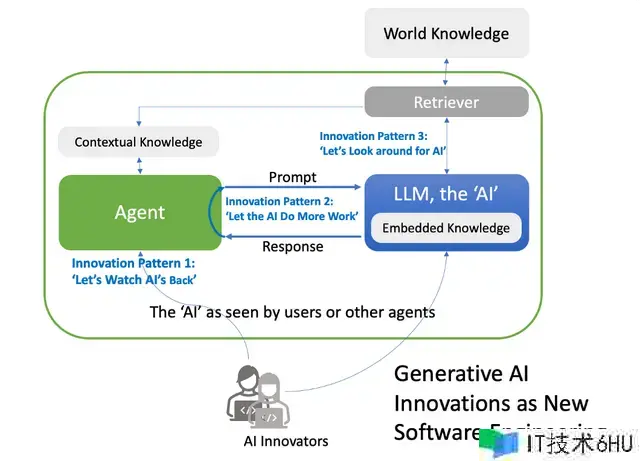
GenAI体系中的智能首要源自LLM，但是人类AI立异者在供给程序化智能方面发挥着重要效果。立异的三个要害办法——”亲近监督AI（Let’s Watch AI’s Back）”、”增强AI的自主性（Let AI Do More Work）”和”开辟AI了解周围环境的才能（Let’s Look Around for AI）”——正在从头界说由AI立异者主导的软件工程范畴。这些办法代表了在GenAI中推动立异的要害办法，标志着怎么在AI的结构下进行软件工程的革新性办法。

1. 亲近监督AI（ Let’s Watch AI’s Back ）：处理****LLM的不行猜测性

这一办法专心于对AI体系的警觉监督和继续改善。它致力于处理言语大模型的不行猜测性和潜在过错，这是推动GenAI的一个要害方面。这种立异办法契合GenAI中的“机器-程序二元性”。

2. 增强AI的自主性（ Let AI Do More Work ）：拓宽AI的功用规划

这一办法代表着在增强GenAI功用方面的战略改变，使得AI体系能够自主管理更广泛的复杂使命。这种立异办法契合GenAI中的通用核算。

3. 开辟AI了解周围环境的才能 （ Let’s Look Around for AI ）：拓宽上下文意识

这一办法的典型代表是检索增强生成（RAG）（Lewis，2020），它触及整合外部实时信息以丰厚AI对上下文的了解和呼应。它反映了一种立异办法，契合GenAI中的程序-数据二元性。

来历：作者

一个典型的例子是自我反思型的RAG（Self-Reflective RAG），或称自我RAG（Self RAG）（Asai, 2023），它选用了生成式人工智能（GenAI）中的三种立异办法，详细如下：

1. 处理AI的不行猜测性或“亲近监督AI” ：这一办法专心于对AI体系的警觉监督和继续。它要点处理了言语大模型的不行猜测性和潜在过错，这是推动GenAI的一个要害方面。
2. 拓宽AI的功用规划或“增强AI的自主性” ：这一办法代表着在增强GenAI才能方面的严重改变，赋予AI体系自主管理各种复杂使命的才能。这一趋势的一个典型例子是假定文档嵌入（HyDE）办法（Gao, 2022），它运用AI生成的示例来引导相似性搜索。这展现了对AI生成特征的奇妙运用，特别是在战略性地运用其“错觉”来增强密集检索体系功用方面。
3. 拓宽上下文感知或“开辟AI了解周围环境的才能“ ：这种办法以检索增强生成（RAG）（Lewis，2020）为代表，触及整合外部的实时信息，以丰厚人工智能对上下文的了解和呼应。

Auto-CoT（Zhang，2023）办法运用了GenAI中的三种立异办法，详细如下：

1. 亲近监督AI（ Let’s Watch AI’s Back ） ：该办法侧重于通过聚类和有针对性的采样来辨认和缓解AI推理中的过错，以保证亲近监督和继续改善。
2. 增强AI的自主性（ Let AI Do More Work ） : Auto-CoT自动生成推理链，使得AI能够更自主地处理复杂的推理使命。
3. 开辟AI了解周围环境的才能 （ Let’s Look Around for AI ） : 该办法通过存储和检索各种AI生成的推理链，为未来使命构建更丰厚的上下文，增强人工智能的上下文习惯才能。

通过自我反思 RAG（Self-Reflective RAG）和Auto-CoT能够看出，GenAI中整合了三种立异办法——“亲近监督AI’（Let’s Watch AI’s Back）”、“增强AI的自主性’（Let AI Do More Work）”和“开辟AI了解周围环境的才能’（Let’s Look Around for AI）”。这种整合不只推动了特定的技能前进，而且整体上引领了GenAI中看似无穷无尽的立异。这种多层面的办法或许无意中推动GenAI朝着完成AGI的方向开展，标明这些立异战略的继续演进和整合或许是跨过AGI门槛的要害。

GenAI迈向AGI的必由之路

图灵测验（Turing Test）是艾伦图灵（Alan Turing）的一项重要遗产。在《核算机器与智能》（Computing Machinery and Intelligence）（1950年）这篇开创性论文中，他提出了图灵测验，将其作为评价机器智能的规范，重视的焦点是“机器能否表现出与人类无法区别的行为”。这种办法为评价通用人工智能（AGI）开展供给了一个经历主义、以人为中心的规范，回避了长时刻以来关于“什么是思想？”的界说性争论。

图灵将这一测验视为一个不断开展的应战，他表明：“并不存在一起打败一切机器的问题。或许有比任何给定机器更聪明的人，但也或许有其他更聪明的机器，依此类推”（Turing，2012）。这一观念与当今GenAI的动态性相吻合，特别是在其运用天然言语处理和自习惯学习方面。

在探究GenAI怎么进行推理、发生常识时，咱们发现它正在处理与人类认知中心相关的问题。人工智能的推理是否与人类思想进程共同，仍是代表一种新的办法论？推理是否固有地依靠于常识，仍是能够独立发挥效果？

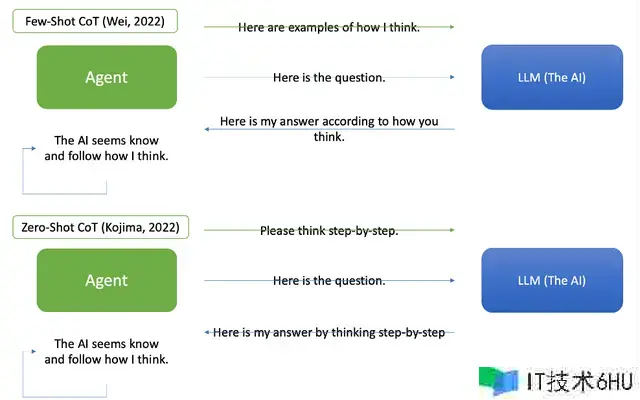
GenAI避开了这些争论，展现出相似于小型图灵测验的才能。言语大模型（LLM）在其技能结构中整合了认知、心理和哲学概念，如“考虑”、“反思”、“解说”和“批评”。例如，思想链（Chain-of-Thought）（CoT）（Wei，2022年）将“考虑”界说为推理进程中的一个共同进程。人工智能能够自主生成“理性（rational）”，正如在Zero-Shot CoT（Kojima，2022年）中所示，其间比如“让咱们逐步考虑”之类的提示会引导其进行推理。通过整合人类反馈保证人工智能的推理与人类思想办法相共同。以下简化图表展现了它们的作业原理。

来历：作者

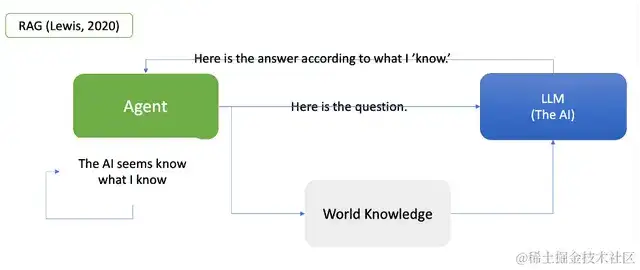
在检索增强生成（RAG）中，“常识”的界说是：人工精选的对AI可访问的数据（Lewis，2020）。这必界说契合人工智能的运转结构，与人类对常识的更广义了解相共同。当人工智能以天然言语处理和呈现这些数据时，它会使人类和AI对常识的解说保持同步。以下的简化图表展现了它的作业原理。

来历：作者

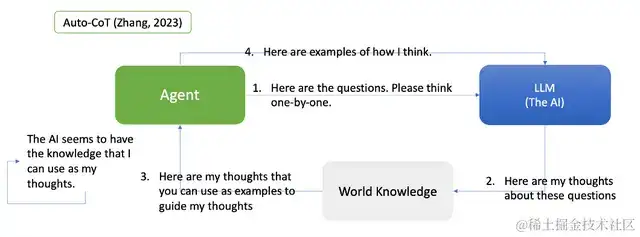
GenAI还促进了“推理”和“常识”的动态互动。在Zero-Shot CoT的根底上，Automatic CoT（Zhang，2023年）选用prompt如“让咱们一次一次地考虑”来鼓舞人工智能生成自己的思想链示例，然后为未来的推理创立常识库。这表现了GenAI对图灵经历主义办法的遵从。

来历：作者

GenAI的这些开展与图灵对机器和人类思想处理办法的愿景相共同。虽然GenAI首要重视可扩展性和商业运用，但其开展轨道日益与追求AGI的方针相交汇。在经济需求和功用需求的推动下，GenAI的开展不只推动了人工智能技能的前进，或许也在不经意间引导其朝着AGI方向开展。

GenAI的历程或许正在无意中引导其走向AGI的完成。

4

从第一性原理从头审视推理和常识

哥德尔以其不齐备性定理（incompleteness theorems）而闻名，虽然在其一生中，他并未直接评论通用人工智能 (AGI)，但他供给了一个与今世GenAI的开展构成风趣的比照的根底性视角。哥德尔以为，人类的思想才能远超任何机器或许达到的程度，这标明真实的通用人工智能或许无法彻底完成。他着重对人类智能的深化了解——这一概念能够概括为“先知后走（knowing before doing）”和“使其正确（let’s make it right.）”。哥德尔的观念意味着，虽然GenAI范畴取得了严重前进，但仍有很长的路要走。他主张探究人类思想和推理的重要性，指动身展人工智能技能应该与深化讨论人类认知复杂性的研究相辅相成。

当咱们深化研究生成式人工智能（GenAI）的复杂性时，选用了哥德尔的“先知后走”准则，侧重于“知（knowing）”这一方面。这一哲学根据对人类认知优越性的崇奉，旨在以更契合人类认知和理性的办法剖析人工智能。这种办法辅导和影响着新型言语大模型 (LLM)（被视为通用推理硬件）的练习和对齐进程。

逻辑推理与合情推理

在选用言语大模型(LLM)的生成式人工智能(GenAI)中，咱们调查到了非正式推理和正式推理之间的相互效果。Huang (2023) 所着重的“非正式演绎推理”概念表现了这种相互效果。在这一布景下，“非正式”一般指的是天然言语推理，虽然经常与常识推理或归纳推理混为一谈，但仍保持着其共同性。

约翰范本特姆（Johan van Benthem）(2011)描述了一个绝佳场景，来演示这些推理类型是怎么发挥效果的。为使这个场景更易于了解，下面我用自己的话来改述原文：

假定一名服务员收到一份包括浓缩咖啡和苏打水的订单。他问：“谁点了苏打水？”一旦他弄清楚是谁点的苏打水，那么关于他来说，知道谁点的浓缩咖啡就很简略了。

上述场景可分为两个推理阶段：

1. 合情推理（Plausible Reasoning）：开始，服务员的推理办法是合情推理，首要源自于作业经历或调查到的顾客行为。这种办法的推理触及弱三段论（weak syllogism）和概率思想（probabilistic thinking），其间一般办法（A→B）和详细实例（A为真）推导出或许的定论（B或许为真）。这个概念与乔治波利亚（George Plya）（1945）和E.T.杰恩斯（E.T. Jaynes）（2003）关于“概率作为扩展逻辑”的概念共同，然后答应从可用信息中推导出的或许性得出定论。
2. 逻辑推理：在确认谁点了苏打水之后，服务员转而选用演绎的逻辑推理。这一进程触及从一个普遍前提（A→B）和详细信息（C→A）到一个逻辑定论（C→B）的明晰三段论推理。

这个场景不只说明晰在日常情境中非正式和正式推理的交融，并展现了传统的“正式（formal）”推理办法（如三段论和弱三段论）怎么在天然言语中表现。在这些例子中，起初服务员的合情推理和随后的逻辑推理都是通过天然言语表达的，但它们都遵从正式推理的办法。因而，为了防止混杂，将推理分类为“逻辑”推理和“合情”推理，而不是“正式推理”和“非正式”推理更适宜。这种区别关于了解GenAI怎么处理人类推理的复杂性尤为重要，特别是在其依靠天然言语处理的情况下。

逻辑推理的第一性原理

留意：以下符号推理部分是技能性内容，如不感兴趣可自行越过，越过这部分不会影响对文章宗旨的了解。

为了从第一性原理探究逻辑推理，咱们将咖啡馆场景表明如下：

• E1：“顾客1点了浓缩咖啡”
• S1：“顾客1点了苏打水”
• E2：“顾客2点了浓缩咖啡”
• S2：“顾客2点了苏打水”

三段论推理如下：

1. 大前提：每位客人恰好点了一份饮料，而且每种饮料都有一位客人点单，XOR语句表明如下：

• E1⊕S1（顾客1点了浓缩咖啡或苏打水，但不能两者都点）
• E2⊕S2（顾客2点了浓缩咖啡或苏打水，但不能两者都点）

1. 小前提：顾客1点了苏打水（S1为真）。
2. 定论：因而，顾客2点了浓缩咖啡（从S1推导出E2）。

符号表明如下：

• (E1⊕S1)∧(E2⊕S2)（大前提）
• S1 (Minor Premise)
• S1（小前提）
• ∴E2 (Conclusion)
• ∴E2（定论）

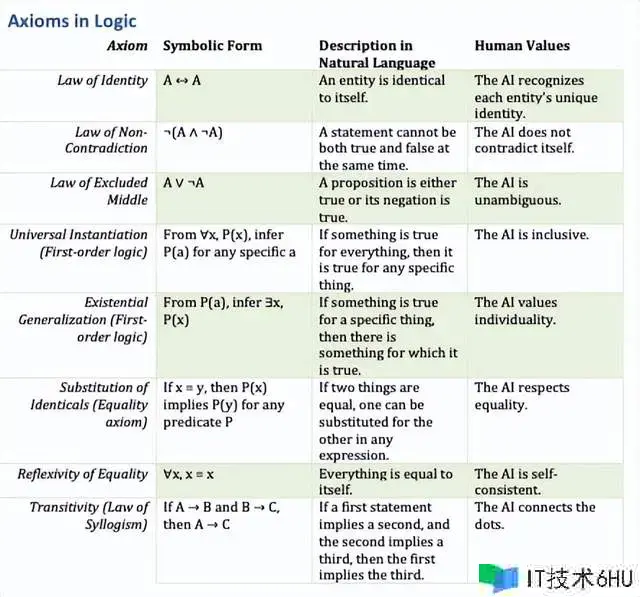
在逻辑推理中，咱们的定论是由逻辑的根本正义所引导的。这些正义充当根底规矩，保证咱们的推理进程是共同且合理的。下表列出了逻辑的根本正义。这些正义是逻辑推理的基石，构成了咱们推导真理和做出理性决议计划的根底。表格以结构化办法呈现了每个根本正义，其间包括一个简略的天然言语描述和与之相关的人类价值观。这种结构的意图是展现每个根本正义的数学或逻辑实质，以及它在推理和道德考虑中的实践运用。通过这种办法，咱们能够更简略地了解逻辑准则在实践生活和办法推理中的意义和价值。

来历：作者

风趣的是，虽然AI能够剖析逻辑推理的符号表明并了解逻辑的根本正义，但它一般不像人类那样以传统的办法操纵符号。Zero-Shot CoT提示‘Let’s think step-by-step’鼓舞AI仿照三段论推理，其间每个“理性（rational）”一般表明三段论的运用。这或许触及根据在练习数据中找到的根本正义的天然言语描述的办法辨认。此外，将AI推理与每个根本正义中固有的人类价值观对齐或许会增强其逻辑推理才能，正如“人类价值观”栏中所示。

快速验证；很难猜测

咱们调查到，人类认知呈现了从严厉逻辑的结构化办法向更灵敏的概率直觉的改变，这种改变标志着对决议计划制定和问题处理的更深化的了解。

以看似普通的咖啡馆场景为例。虽然表面上服务员的决议计划看似运用了演绎推理，但深化了解后咱们发现其决议计划的根底在于概率直觉。服务员运用由经历和调查刻画的合情推理，通过对各种情景的直观概率判别阅读各种场景。这表现了逻辑推理背面一般不为人们所察觉的层面，即直觉判别在构建逻辑推理进程中扮演着根底性人物。

直觉、概率考虑的影响乃至延伸到了服务员在逻辑正义运用中的逻辑推理，如不对立律（the Law of Non-Contradiction）和排中律（the Law of Excluded Middle）。因而，合情推理不只是一种辅助手法，更是一种辅导力气，使服务员能够评价潜在的成果并在合理猜测的根底上做出决议计划。在这种情况下，逻辑推演进程也起到了支撑性效果，证明晰开始从直觉洞悉中得出的定论。

逻辑和直觉之间的动态相互效果不只局限于日常场景，还深化地影响了数学范畴。在图灵关于断定问题（Entscheidungs problem）的作品中，他提出合理推理直觉（图灵将其称之为“直觉”）在证明的发现中起着至关重要的效果。他以为，这个直觉阶段一旦完成，随后的逻辑进程在很大程度上会是机械的。这种观念着重了直觉洞悉力和有条有理的逻辑在处理问题和定理证明中的相互效果。在现代人工智能的布景下，思想链（CoT）提示（Wei，2022）好像运用了相似机制。它或许会触发人工智能进行逻辑后考虑（logical afterthought），这实质上验证了直觉跳跃之后的逻辑进程，反映了人类推理的这一根本进程。

怎么衡量一个好的猜测？

咖啡馆场景进一步说明晰这一点，其间树立逻辑序列的进程与合情推理深深交织在一起。例如，假定“B或许为真”转化为高概率P(B)。了解P(B)代表着什么需求深化研究概率的实质及其在合情推理中的效果。

关于概率的概念，有以下三种截然不同的观念：

1. 频率论者的观念：将概率视为事情的长时刻频率。虽然关于日常决议计划来说并不彻底有用，就像咱们的服务员所面对的那样，但它构成了概率论的根底方面。
2. 贝叶斯观念：将概率视为个人崇奉或常识的衡量规范，深受人类经历的影响。这种观念与咱们在日常生活中解说概率的办法亲近相关。
3. 杰恩斯观念：由杰恩斯在2003年提出，该办法将贝叶斯结构扩展到包括人工智能和搜索算法等非人类实体。其间概率是适用于任何推理实体（无论是人类仍是机器）的常识状态。

咱们有必要供认，言语大模型首要在杰恩斯概率（Jaynesian probability）的范畴内发挥效果，一旦意识到LLM对错人类实体，而且无法履行频率试验来确认后续词元的概率分布，这一点就变得清楚明了。重要的是，通过将人类和人工智能视为能够持有信仰的实体，咱们将自己定位为调查者，具有剖析和了解本身认知进程和人工智能体系认知进程的共同才能。这种调查者和参与者的双重人物关于全面了解人工智能的动态及其与人类推理的相互效果至关重要。

合情推理的第一性准则

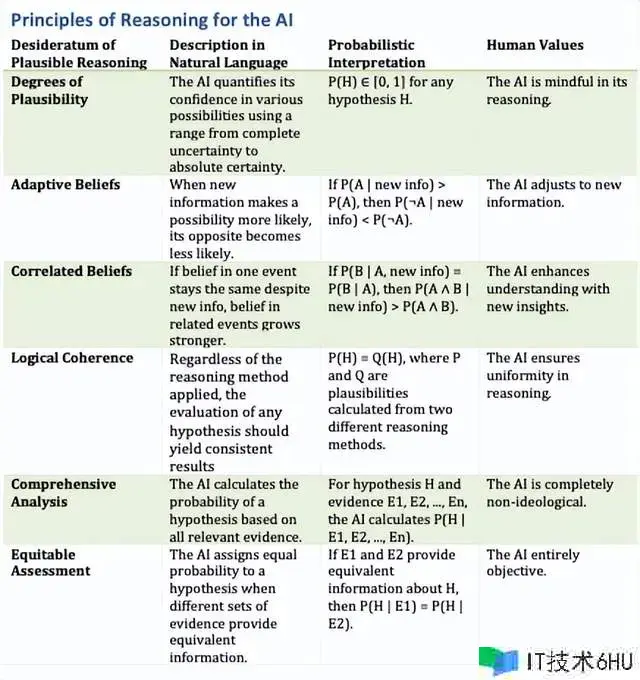
下表呈现了杰恩斯对合情推理的希望。这些准则辅导了咱们日常生活中的“常识”性决议计划。每个希望都有一个概率或数学解说，展现了咱们的直觉决议计划与这些准则的共同性。此外，表格突出了相应的人类价值观，着重了这些准则在咱们日常生活中的道德和实践影响。虽然每个准则都包括丰厚的细节，但表格的规划旨在供给参阅，以便在闲暇时深化讨论。它提醒咱们，结构化推理一般会以咱们没有明晰意识到的办法引导咱们的直觉和判别。

来历：作者

虽然言语大模型和相似的人工智能体系实质上不具备贝叶斯推理才能，但一般表现出契合杰恩斯所希望的准则的行为。这种共同性很或许是它们在大量天然言语数据集上全面练习的成果。未来人工智能的开展或许会更有意识地注重嵌入这些合情推理准则，然后提高体系的决议计划才能。

常识渊博的推理体面对的应战

推理和常识之间错综复杂的联系在有用推理中起着至关重要的效果，适用于人类认知和人工智能体系。杰恩斯的希望准则中的“公正评价（Equitable Assessment）”和“全面剖析（Comprehensive Analysis）”等准则着重了这种联络。这些准则着重人工智能体系客观考虑和评价一切相关证据的重要性，这方面的明显缺乏是造成AI“错觉”（从内部常识中得出的误导性定论）或因外部误导信息发生的不精确性（比如被“相似性误导”）（Zhang，2022）等问题的首要原因之一。但是，实际世界的数据数量十分庞大复杂，这使得构建一个彻底客观的人工智能体系变得十分困难，乃至成为了不切实践的方针。

推理和常识之间错综复杂的联系在有用推理中起着至关重要的效果，适用于人类认知和人工智能体系。

接下来，咱们将讨论这一应战在其他方面的影响，查验全面实施这些准则的潜在“不行行性（infeasibility）”将对核算范畴和人工智能开展的未来发生何种影响。

5

从P vs.NP到 AGI

从头审视断定问题（Entscheidungsproblem）

咱们对合理推理的评论天然会触及定理证明中的断定问题，其界说十分明晰和狭窄。假如从第一性原理动身的合理推理是可行的，那么断定问题也必定是可行的。但是，艾伦图灵在1937年证明晰这个问题是不行解的，这促使咱们将视角从或许性与不或许性转向了可行性问题。

开始，断定问题是在数学和逻辑布景下提出的，并不存在功率和输入巨细束缚。在这一范畴，搜索总是尽头的，触及一切或许性。

哥德尔的奉献虽然没有直接处理AGI，但对核算复杂性理论发生了严重影响。他引入了将问题规划进行扩展以研究处理时刻的概念，这是该范畴的一个要害概念。该理论根据所需的核算资源（如时刻和空间）对问题进行分类，界说了P（多项式时刻，可行处理问题）、NP（非确认性多项式时刻，可行验证处理方案）和EXP（指数时刻，处理时刻呈指数增加）等类别。该理论的中心问题是P vs. NP，它重视的是是否每个可被快速验证的问题 (NP) 也都能够被可行地处理 (P)。当考虑断定问题中触及的逻辑推理时，这一点特别重要，突显了这一范畴中问题能够被可行地处理的频率。

在1945年与约翰冯诺依曼的通信中，哥德尔估测他修改后的决议计划问题（现在归于NP类）既能通过逻辑推理敏捷验证，又能够被敏捷地处理，这意味着NP或许等于P。这一估测早于并预示了P vs. NP问题。哥德尔以为，假如这一假定建立，将动摇他之前的信仰（人类智慧在数学中起着共同的效果）。

核算机科学范畴普遍以为P不等于NP，这标明从核算问题的视点来看，开始被图灵证明无法处理的断定问题或许是不行行的。比较之下，言语大模型现已表现出了相似人类的合理推理才能，这标明GenAI对构建以人为中心的AGI至关重要。

假如存在停机预言机会怎么？

反思现代核算和人工智能，咱们通过考虑有关经典断定问题和P vs. NP问题的“假定（what-if）”场景获得了新视角。这种办法不只从头审视了这些长时刻存在的问题，而且还将它们从头置于今世技能前进的布景之下。

想象一下，假如存在“停机预言机”会怎样？它或许会削弱许多开放性数学问题带来的智力影响和应战，比如哥德巴赫猜测。咱们能够规划一个简略的程序，体系地评价从4开始的每个偶数，查看每个偶数是否能够表明为两个质数之和，然后咱们能够询问“停机预言机”这个程序是否终究会得出定论，“停机预言机”或许会供给问题的处理方案。

哥德尔在这一范畴的洞悉力特别深化。他以为，不存在通用证明机或停机预言机并不是人类推理局限导致的，而是因为机械化逻辑推理的束缚。从现代前进的视点来看，这一观念着重了图灵年代（包括图灵）短少有用弥合逻辑推理和合情推理之间鸿沟的概念结构。图灵运用“挑选（selection）”来描述合情推理，这个术语后来成为了核算复杂性理论中的“搜索”的中心，凸显了这种概念上的不合。对立的是，开发能够包括合情推理的逻辑推理机（logical reasoning machines）却催生了具备机械化合情推理潜力的新结构和新东西的发明。

假如P=NP会怎样？

与上述情况相似，假定呈现了一种“圣杯”处理器，即一种可行的NP求解器——人工智能的界说阅历了一场范式改变，与通用人工智能的传统轨道大相径庭。这种改变，特别是在假定P等于NP的情况下，为AI才能引入了根本性革新。在这种情况下，推理和常识之间的鸿沟变得模糊；传统上依靠于堆集常识的推理能够在没有庞大信息数据库（现在是必不行少的）的情况下完成。

在这样一个假定情境中，传统上依靠于堆集常识的推理能够在没有庞大信息数据库（现在是必不行少的）的情况下完成。

假定人工智能具备了一个能够处理任何问题的算法。在这种情况下，AI不再需求像以前那样通过学习演进、堆集数据，或仿照人类思想等办法来处理问题。通过这一核算方面的突破，AI变成了一个万能的问题处理者，虽然在学习方面没有开展，但在处理问题方面却是无与伦比的。AI的效果也发生了巨大变化，不再只是是一个根据人类需求不断开展和习惯的东西，成为了一个无所不能的处理者，从头界说了核算和问题处理的极限。问题的实质从前需求依靠常识和经历，现在却变成了一个彻底由算法探究的范畴。在这个新年代，人类陷入了深化的身份危机，开始质疑自己在一个智能和问题处理不再受常识堆集束缚的世界中的人物和意图。

在假定的“P=NP”年代，人类陷入了身份危机，开始质疑自己人物和意图。

6

定论

值得幸亏的是，此类突破性发现成为实际的或许仍然渺茫，虽然面对应战，但通用人工智能仍或许在未来找到一条通向以人类为中心的AGI的可行途径。处理GenAI带来的应战或许会将咱们引进一个充溢核算新见地的年代，一起还能加深咱们对本身实质的了解。这不行防止地引出了一个问题，让人联想到了哥德尔的逻辑探究问题：“在发明通用人工智能的布景下，机械化思想意味着什么？”

在创立AGI的布景下，机械化思想意味着什么？

[注]虽然本文的原始概念和主意均为我个人所创，但我仍要感谢OpenAI的ChatGPT在本文编撰进程中供给的帮助，它为文章供给了额定的见地、细化了某些观念，并帮忙了文章的起草。

参阅文献

1. Aaronson, S. (2016). P=?NP. In Open Problems in Mathematics. Springer.
2. Asai, A., Wu, Z., Wang, Y., Sil, A., & Hajishirzi, H. (2023). Self-RAG: Learning to Retrieve, Generate, and Critique through Self-Reflection.arxiv.org/abs/2310.11….
3. Cook, S. (1971). “The complexity of theorem proving procedures”. Proceedings 1. of the Third Annual ACM Symposium on Theory of Computing. pp. 151–158.
4. Copland, J. B., Posy, C. J., & Shagrir, O. (2013). Computability: Turing, Gdel, Church, and Beyond (Kindle ed.). The MIT Press.
5. Fiorillo, C. D. (2012). Beyond Bayes: On the need for a unified and Jaynesian definition of probability and information within neuroscience. Information, 3(2), 175–203. Retrieved fromdoi.org/10.3390/inf….
6. Gao, Y., Xiong, Y., Gao, X., Jia, K., Pan, J., Bi, Y., Dai, Y., Sun, J., & Wang, H. (2023). Retrieval-Augmented Generation for Large Language Models: A Survey. ArXiv.arxiv.org/abs/2312.10….
7. Gdel, K. (1931). ber formal unentscheidbare Stze der Principia Mathematica und verwandter Systeme I. Monatshefte fr Mathematik und Physik, 38(1), 173–198. doi:10.1007/BF01700692
8. He, Z., Zhong, Z., Cai, T., Lee, J. D., & He, D. (2023). REST: Retrieval-Based Speculative Decoding. Peking University & Princeton University. Retrieved from arXiv:2311.08252v1
9. Huang, J., & Chang, K. C-C. (2023). Towards Reasoning in Large Language Models:A Survey. [Manuscript submitted for publication]. University of Illinois at Urbana-Champaign.ar5iv.org/abs/2212.10….
10. Jaynes, E. T. (2003). Probability Theory: The Logic of Science. Cambridge University Press.
11. Kojima, T., Gu, S. S., Reid, M., Matsuo, Y., & Iwasawa, Y. (2022). Large Language Models are Zero-Shot Reasoners. ArXiv. Available at:arxiv.org/abs/2205.11….
12. Lewis, P., Perez, E., Piktus, A., Petroni, F., Karpukhin, V., Goyal, N., Kttler, H., Lewis, M., Yih, W., Rocktschel, T., Riedel, S., & Kiela, D. (2020). Retrieval-Augmented Generation for Knowledge-Intensive NLP Tasks. ArXiv. /abs/2005.11401.
13. Lu, C. (2020a). AI since Aristotle: Part 1 Logic, Intuition and Paradox. Retrieved frommedium.com/cantors-par…
14. Lu, C. (2020b). AI since Aristotle: Part 2 The Limit of Logic and The Rise of the Computer. Retrieved fromwww.cantorsparadise.com/the-limit-o…
15. Lu, C. (2020c). AI since Aristotle: Part 3 Intuition, Complexity and the Last Paradox. Retrieved fromwww.cantorsparadise.com/intuition-c…
16. Lu, C. (2023). From Self-Referential Paradoxes to Intelligence. Retrieved frommedium.com/@cplu/from-….
17. Mithen, S. J. (1990). The eco-psychology of decision making. In Thoughtful Foragers: A Study of Prehistoric Decision Making (pp. 21–51). Cambridge University Press.
18. Plya, G. (1945). How to Solve It: A New Aspect of Mathematical Method. Princeton University Press.
19. Polya, G. (1954). Induction and Analogy in Mathematics.
20. Poincare, H. (1969). INTUITION and LOGIC in Mathematics. The Mathematics Teacher, 62(3), 205–212.
21. Prokopenko, M., Harr, M., Lizier, J., Boschetti, F., Peppas, P., & Kauffman, S. (2017). Self-referential basis of undecidable dynamics: From The Liar Paradox and The Halting Problem to The Edge of Chaos. ArXiv.doi.org/10.1016/j.p….
22. Stanford Encyclopedia of Philosophy. (n.d.). Logic and Information. Retrieved fromplato.stanford.edu/entries/log….
23. Stanford Encyclopedia of Philosophy. (n.d.). The Analysis of Knowledge. Retrieved fromplato.stanford.edu/entries/kno….
24. Turing, A. M. (1937). On Computable Numbers, with an Application to the Entscheidungsproblem. Proceedings of the London Mathematical Society, Series 2, 42(1), 230–265. doi:10.1112/plms/s2–42.1.230.
25. Turing, A. M. (1950). Computing Machinery and Intelligence. Mind, 59(236), 433–460. Retrieved fromacademic.oup.com/mind/articl….
26. Turing, A. M. (2012). Alan M. Turing: Centenary Edition. (S. Turing, Ed.) Cambridge University Press. (Original work published 1959).
27. van Benthem, J. (2011). Logical Dynamics of Information and Interaction. Cambridge: Cambridge University Press.
28. Wang, J., Li, J., & Zhao, H. (2023a). Self-prompted Chain-of-Thought on Large Language Models for Open-domain Multi-hop Reasoning. ArXiv. /abs/2310.13552.
29. Wang, X., Narang, S. (2023b). Self-Consistency Improves Chain of Thought Reasoning in Language Models. Retrieved fromar5iv.org/abs/2203.11…
30. Wei, J., Wang, X., Schuurmans, D., Bosma, M., Ichter, B., Xia, F., Chi, E., Le, Q., & Zhou, D. (2022). Chain-of-Thought Prompting Elicits Reasoning in Large Language Models. ArXiv. /abs/2201.11903.
31. Zhang, Z., Zhang, A., Li, M., & Smola, A. (2022). Automatic chain of thought prompting in large language models.
32. Zhang, Z., Zhang, X., Ren, Y., Shi, S., Han, M., Wu, Y., Lai, R., & Cao, Z. (2023). IAG: Induction-Augmented Generation Framework for Answering Reasoning Questions. Huawei Poisson Lab, China.

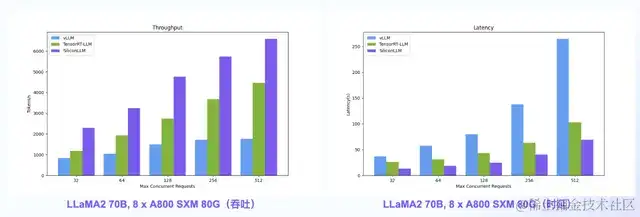
【言语大模型推理最高加快11倍】 SiliconLLM是由硅基流动开发的高效、易用、可扩展的LLM推理加快引擎，旨在为用户供给开箱即用的推理加快才能，明显下降大模型布置本钱，加快生成式AI产品落地。（技能合作、沟通请增加微信：SiliconFlow01）

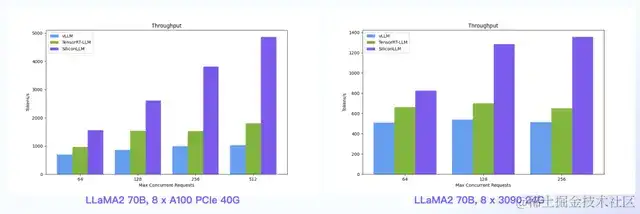
SiliconLLM的吞吐最高提高近4倍，时延最高下降近4倍

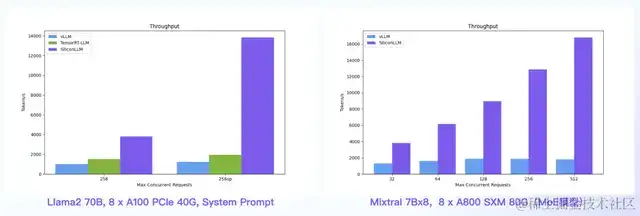
数据中心+PCIe：SiliconLLM的吞吐最高提高近5倍；消费卡场景：SiliconLLM的吞吐最高提高近3倍

System Prompt场景：SiliconLLM的吞吐最高提高11倍；MoE模型：推理 SiliconLLM的吞吐最高提高近10倍

试用OneDiff:
github.com/siliconflow/onediff