好久没翻译文章了，感觉自己的英文功底有点下降，前几篇文章都着眼于网络I/O了，这篇文章之后咱们开端亮点数据库、数据结构之类的内容。

原文链接: blog.allegro.tech/2023/11/how…

已经征得作者的同意能够进行翻译。

B-树是一种查找很多数据的结构，发明于四十年前，现在依然被用于现代的数据库。尽管已经有了一些新的索引结构，像LSM(Log-Structured-Merge-Tree)树， 在处理大多数数据库查询的时分，B-树依然是无与伦比的。

阅览本篇文章之后，你将会了解B-树怎么组织数据以及怎么履行查找查询。

译者注, LSM树并不像是B树、红黑树相同是严格的数据结构，其实是一种存储结构，现在HBase,LevelDB,RocksDB这些NoSQL存储都是采用的LSM树)

源起

为了让咱们了解B-tree，让咱们先来将目光放在二叉查找树

等等，这难道不是相同的吗？

那B-树的B代表什么?

依据维基百科， B-树的发明者 Edward M. McCreight曾经说过:

你越是考虑B-树的B代表些什么，就能越能了解B-树。

把B-树和二叉查找树混为一谈是一个十分遍及的误解，不管怎么，在我看来，二叉查找树是重塑B-树的一个很好的起点，让咱们先从一个十分简略的二叉查找树开端:

B-树怎么让你的查询更快

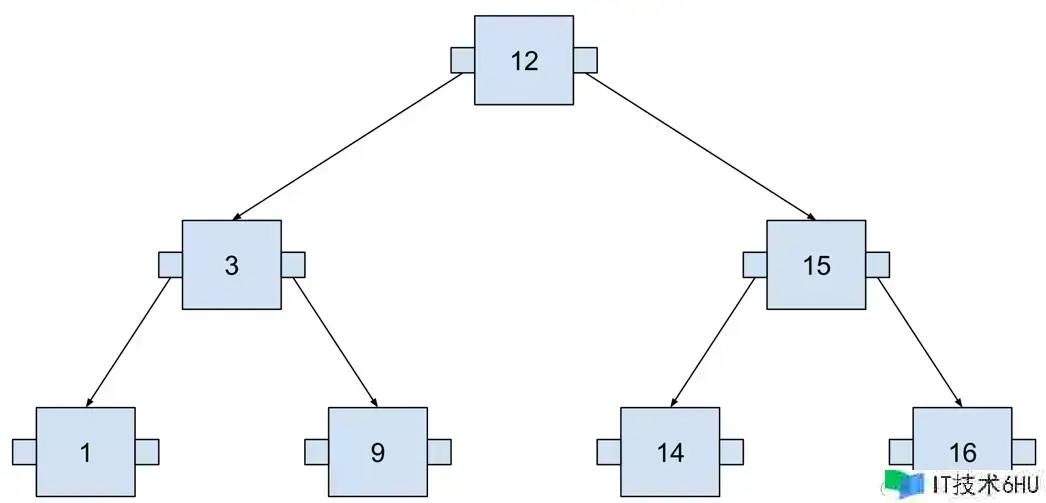
右边节点的数字总是比双亲节点要大，左边节点的数据总是比双亲节点的小。咱们再增加一些数字会变得再明晰一些。

B-树怎么让你的查询更快

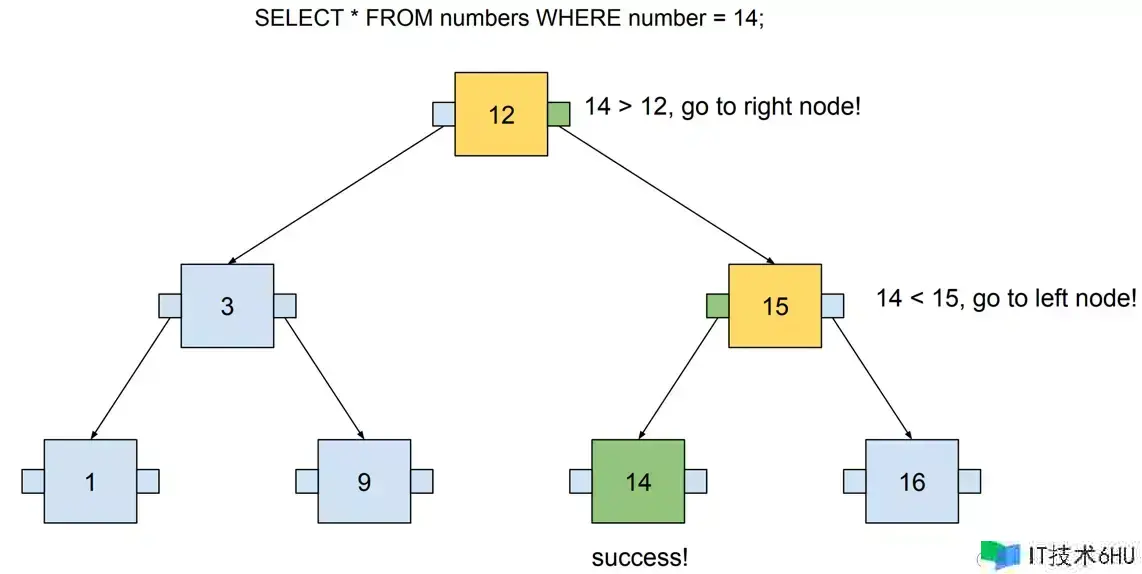
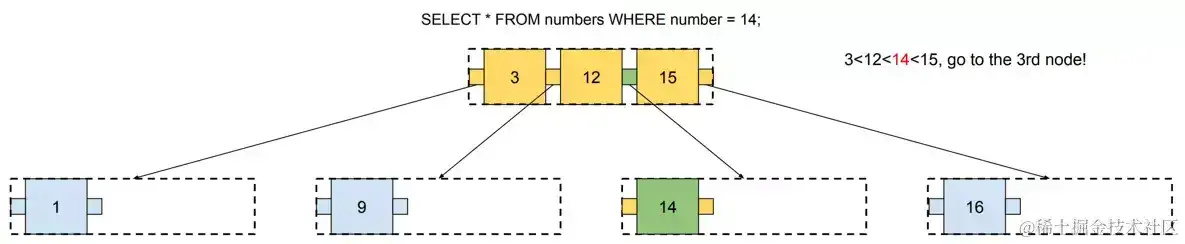
现在这颗二叉查找树包括七个节点，可是咱们最多需求拜访三个节点才能找到咱们想要找到的数字，下面示例查找14这个数字的进程，这里我运用SQL去界说查询，以便将这棵树视为实践数据库索引。

B-树怎么让你的查询更快

硬件

理论上来说，运用二叉查找树来运行咱们的查询看起来没有问题，它的查找花费的时刻复杂度是O(logn)，和B-树相同。然后，在实践中，数据结构需求工作在实践的硬件上。索引必须存储在你机器上的某个方位上。

核算机有三个方位存储数据:

  • CPU缓存
  • RAM(memory) 内存
  • Disj(存储) 磁盘

缓存彻底被CPU管理。此外，它相对较小，一般只要几兆字节。索引或许包括几千兆的数据，所以这里不适合。

数据库很多运用内存，内存有一些十分棒的长处:

  • 快速随机存取(将在下一章节介绍)
  • 容量能够十分大(（例如，AWS RDS 云服务供给可用内存为几 TB 的实例)

缺陷是断点的时分会丢掉数据，而且相关于磁盘，它适当贵重。

最终内存的缺陷便是存储器的长处，它很廉价，即使断电数据也会保留在那里。可是，天下没有免费的午餐，问题在于咱们需求谨慎对待次序拜访和随机拜访。只要在指定的条件下，磁盘读取数据才会很快。我会试着简略解说一下。

随机拜访和次序拜访

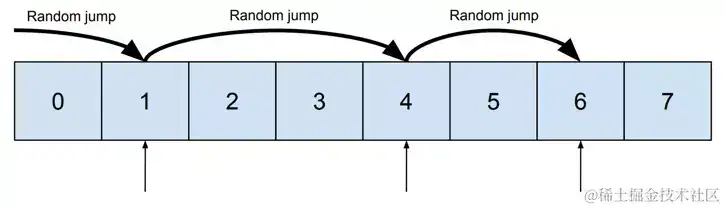
内存能够形象的了解为一排排存放数值的容器，每个容器有对应的编号。

B-树怎么让你的查询更快

现在让咱们假定咱们需求从编号1,4,6这三个容器上读取数据，这需求随机拜访:

B-树怎么让你的查询更快

然后和读编号为3,4,5的容器进行比较，它就能够按次序完结。 随机跳转和次序读取的不同能够用磁盘驱动器来解说，磁盘由磁头和磁盘组成。

B-树怎么让你的查询更快

“随机跳转”要求磁头移动到磁盘上的指定方位。“次序读取”只需求旋转磁盘，让磁头读取接连的值， 在读取兆字节的数据时，这两种拜访方法之间的距离是巨大的。运用”次序读取“能够大大的降低获取数据所需的事情。

Adam Jacobs宣布在Acm Queue上宣布的文章“The Pathologies of Big Data” ，研讨了随机拜访和次序拜访在速度上的差异。文章揭示了一些令人震惊的实践。

  • 次序拜访在机械硬盘上的拜访速度比随机拜访快几十万倍。

  • 从磁盘次序读取有或许比从内存读取更快

可是现在谁还用机械硬盘？ 那固态硬盘呢? 这项研讨显示机械硬盘上的次序彻底读取数据或许比固态硬盘更快。不过请注意，这篇文章是2009年的，而固态硬盘在过去十年得到了持久的开展。这些结果或许已经过时了。

总之，关键就在于便是尽或许挑选次序拜访。下一个章节，咱们将解说怎么将其应用到咱们的索引结构上。

优化对树的次序拜访

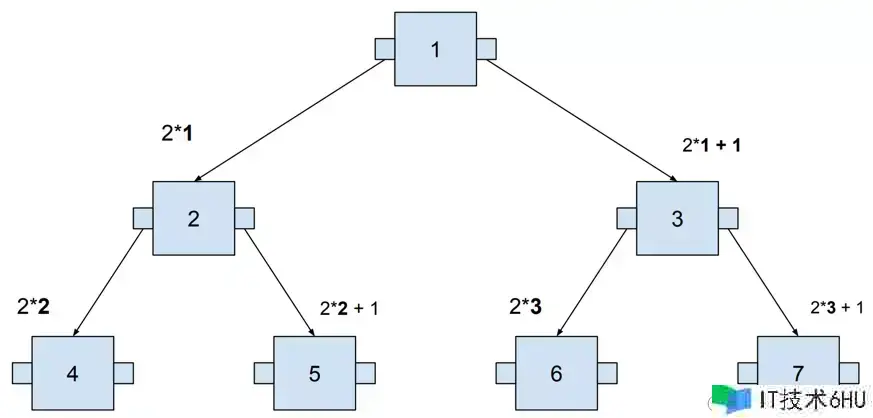
  • 二叉查找树在内存中的表明办法和堆相同

    • 父节点的方位是i

    • 左节点的方位是2i

    • 右节点的方位是2i + 1

这是依据示例核算出来的方位(父节点从1开端)

B-树怎么让你的查询更快

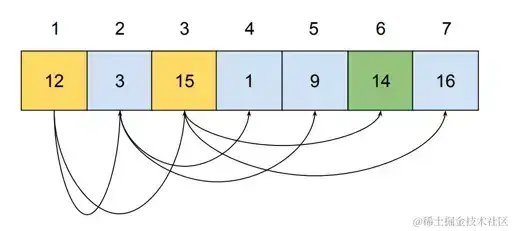
依据被核算出来的方位，节点被对齐到内存中

B-树怎么让你的查询更快

你还记得咱们前面评论的可视化查询吗?

B-树怎么让你的查询更快

这便是在内存级别的样子:

B-树怎么让你的查询更快

履行查询的时分，内存地址1,3,6会被拜访，拜访三个节点不是问题，可是，假如咱们存储了更多数据，这棵树就或许变得更高。存储超越100万个值需求一颗高度至少为20的树。这意味着必须从内存不同方位读取20个值，这会导致彻底的随机拜访。

页面

树在增高的一起，随机拜访会导致越来越多的推迟。解决这一问题也很简略: 让树变宽而不是高度增长。能够经过将多个值打包到一个节点来完成。

​ 它有以下好处：

  • 树更浅，两层而不是三层。

  • 依然有很多的空间能够容纳新的值，而无需进一步增长。

在这种索引上履行查询如下图所示:

B-树怎么让你的查询更快

请注意每次咱们拜访一个节点，咱们都需求加载这个节点一切的值，在这个比如中，咱们需求加载4个值(假如树是满的，就需求6个值)才能找到咱们需求的值。下面是这棵树在内存中的展现

B-树怎么让你的查询更快

与上一个示例相比(树的高度不断增加)，查找应当更快，咱们仅需求随机拜访两次(跳转到0和9单元)，然后次序读取剩余的值。

  • 二叉查找树的有20层

  • 只要10层的3值节点树。

单个节点的值构成一个页面，在上面的比如中，每个页面由三个值组成。页面是磁盘上一组相邻的值，因而数据库进需求一次次序拜访读取，就能一起读取整个页面，

它与实践又是怎么联系的呢？ Postgres的页面巨细只要8kb，假定20%是元数据，那么还剩余6kb。页面的一半需求存储指向子节点的指针，所以给咱们存储值剩余的空间就只剩余3kb，BIGINT的巨细是8 bytes，因而咱们能存储375个值再单个页面里边。

假定数据库有一些超级大的表有10亿条记录，那么咱们在postgres树种需求多层才能存储? 依据上面的核算，单个节点能够存储375个值，它能够只要四层的树来存储10亿个值。关于如此很多的数据，二叉查找树将需求30层来存储。

总之，在单个节点里边存储放置多个值有助于咱们能够减少树的高度。咱们因而就能从次序拜访中受益。然后B-树不只能够增加高度，也能够经过增加页面巨细来增加宽度。

平衡

在数据库中有两种根本的操作: 写和读。在上一节中咱们评论了从B-树中读取数据的问题。可是写入数据也是一个十分关键的点，向数据库中写入数据的时分，B-树需求不断更新新值。

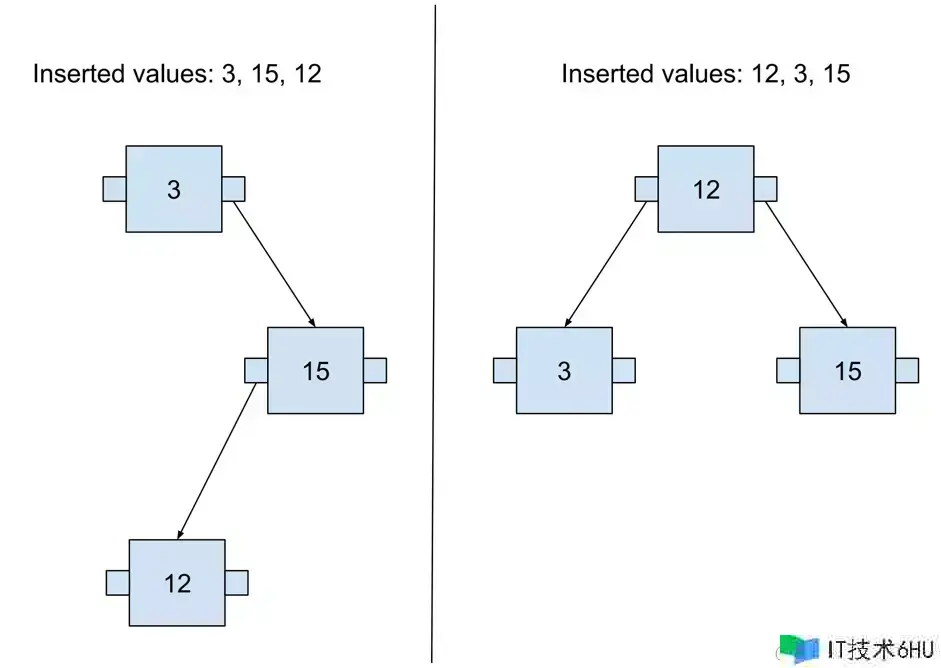
树的形状取决于增加进入树的值的次序，这在二叉树中很容易看到，假如数值增加次序不正确，咱们或许会得到不同深度的树。

B-树怎么让你的查询更快

当树在不同节点上具有不同的深度时，它被称为不平衡树，有两种方法能够将这样的树恢复到平衡状况。

  1. 重新构建这棵树，依照正确的次序增加值。

  2. 在增加新值的时分一起坚持平衡。

B- 树挑选了第二种方案，使树始终坚持平衡的特性称之为自平衡。

自平衡算法示例

构建B-树能够简略的从创立一个独自的节点开端，并不断的增加新值，直到节点里边没有闲暇空间停止。

B-树怎么让你的查询更快

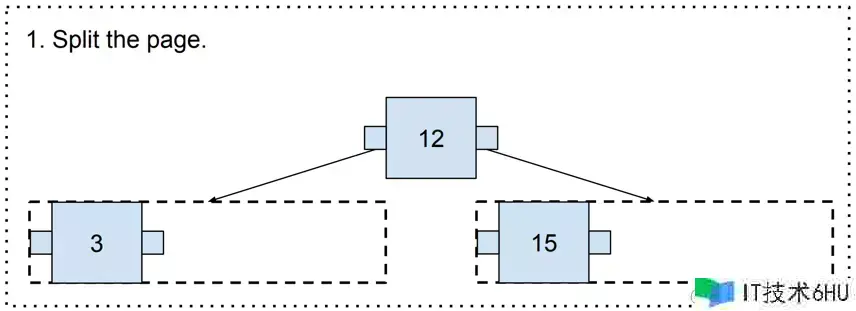
假如相应的页面没有空间，就需求进行页割裂，为了履行割裂，需求挑选一个“割裂点”，在这种情况下挑选的割裂点将会是12，因为12处于3和15的中心，割裂点将会是一个移动到上个页面的值。

B-树怎么让你的查询更快

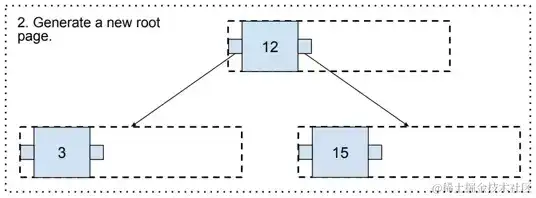
现在，咱们遇到了一个有趣的问题，即没有上层页面，在这种情况下需求生产一个新的页面，割裂点将成为新的根页面。

B-树怎么让你的查询更快

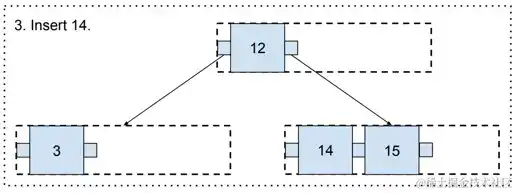
最终，3地点的页面有一些剩余空间，因而能够将14增加进去。

B-树怎么让你的查询更快

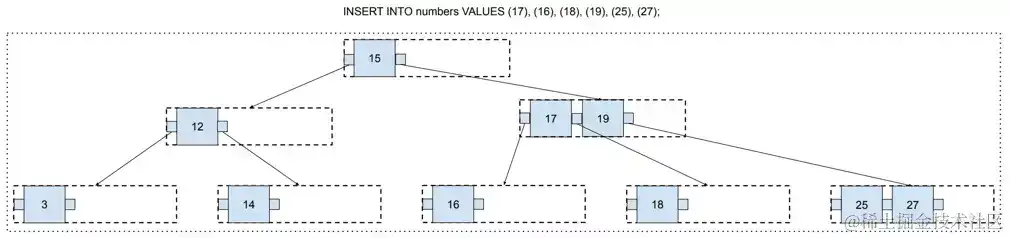
依照这种算法，咱们能够不断向B-树里边增加新值，而B树会一向坚持平衡。

B-树怎么让你的查询更快

在这一点上，你或许会有一些合理的担忧，会有很多闲暇空间没有机会被填满，例如，14、15、16位于不同的页面上，所以这些页面将永久只要一个值和两个闲暇空间。

这是因为割裂方位的挑选引起的，咱们总是将页面从中心割裂。可是，每次进行割裂时。咱们能够挑选咱们想要的任何割裂方位。

Postgres在履行页割裂的时分会履行一个算法，对应的完成能够在Postgre源代码中的bt_findsplitloc()找到完成(见参考链接)

总结一下

在这篇文章里边，你学习到B-树是怎么工作的，总的来说，它能够被简化为一颗具有两个变化的二叉查找树。

  • 每个节点包括超越一个值

  • 刺进新的值的时分，会有一个自平衡算法。

尽管现代数据库用的是B-树的某个变体(像是B+树)，它们依然基于原始概念。我的观念是，B-树的一个巨大优势是它是为在实践硬件上存储很多数据而设计的。这或许是B-树在这么长的时刻里边依然陪伴着咱们的原因。

译者对B-树和B+树的了解

我以为B-树和B+树最主要的差异在于非叶子节点是否存储数据:

  • B树: 非叶子节点和叶子节点都会存储数据
  • B+树: 只要叶子结点才会存储数据，非叶子节点存储键值。叶子节点之间运用双向指针连接，最底层的叶子节点之间形成了一个有序的双向链表。

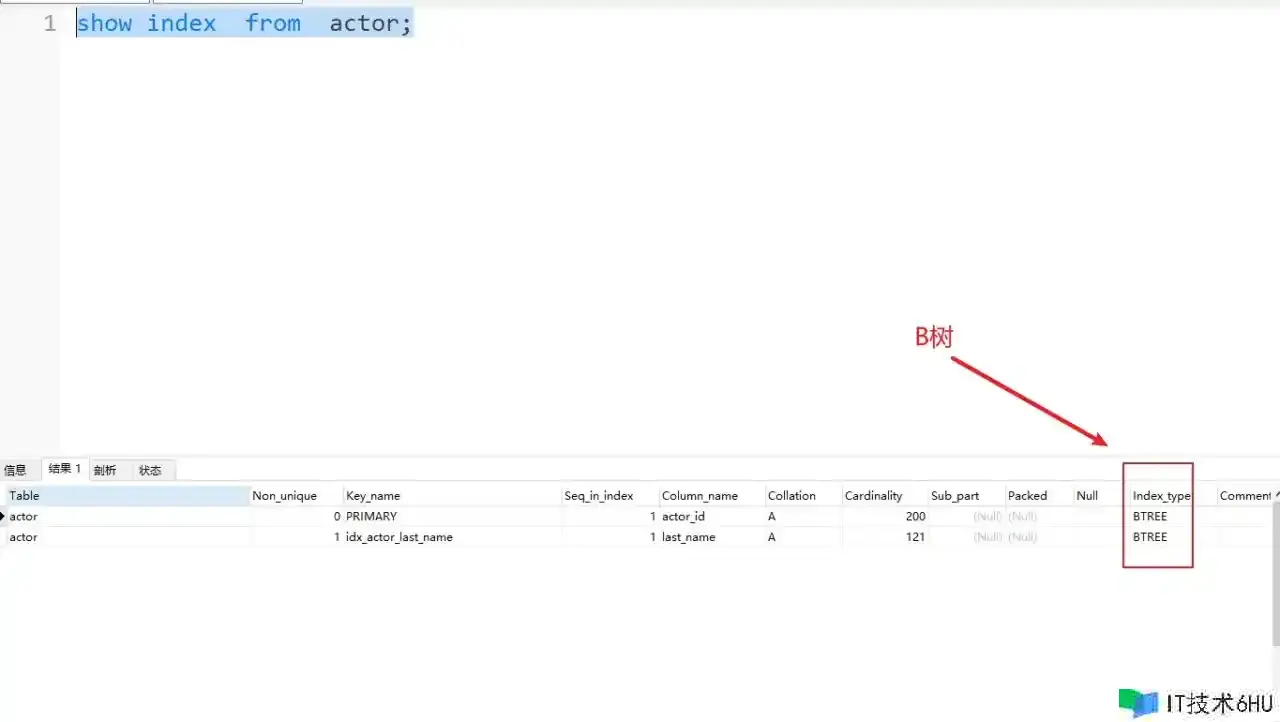
想起之前看B站UP主颜群教师讲课的视频《SQL优化（MySQL版；不适合初学者，需有数据库根底）》, 在讲MySQL索引的数据结构的时分，说MySQL用的是B数，弹幕有人说，教师讲错了吧，应该是B+树，这种认知建立在没有精确了解B-树和B+树之间的联系上，B+树是B-树的变体，也便是说B+树在B-树之上固化了只要叶子节点才会存储数据，非叶子节点存储键值这个特定。在这个意义上，B+树是B-树的一个特例，倒是没那么多的距离，比如安卓与miui，miui也对安卓进行了深度定制，可是咱们说miui是安卓体系也不错。MySQL的开发人员好像也是这么以为的，以为MySQL普通索引的数据结构还是B-树的一个变体，能够取B+树，可是说是B-树也不能算错，这一点能够经过:

// actor 是我在MySQL里边建的一张表,会输出这张表的索引信息，里边展现出了索引的数据结构是B树
show index  from  actor;

B-树怎么让你的查询更快

有些人的了解或许便是两个姓名对应两个概念便是两个不同的事物，假如A概念是从B概念衍生而来，仅仅固化了B概念的一个特点，那么说A是B好像也没什么问题，当咱们评论的再精确一些，评论到具体的完成的时分，咱们就能够发明一个概念专门为了评论问题方便，这也便是B-树和B+树之间的联系。

翻译参考资料

[1] LSM树详解 zhuanlan.zhihu.com/p/181498475

[2] 了解Mysql索引原理及特性 | 京东物流技术团队 juejin.cn/post/731162…

[3] DT讲堂-颜群的JAVA课 space.bilibili.com/326782142?s…

[4] 《SQL优化（MySQL版；不适合初学者，需有数据库根底）》 www.bilibili.com/video/BV1es…