《算法图解》是一本算法入门书，讲解了一些轻松有趣的算法。

第一章：算法简介

二分查找

二分查找算法一次排除一半的或许性，在有序列表查找时，功率比从头开始查找快许多。

大 O 表明法指出了算法的增速。大 O 表明法指出了最糟状况下的运转时刻。除了最糟状况下的运转时刻外，还应考虑均匀状况的运转时刻。

二分查找（Binary Search）是一种在有序数组或列表中查找特定元素的查找算法。它的基本思维是不断将待查找规划缩小为一半，直到找到方针元素或确认方针元素不存在为止。

二分查找的作业原理如下：

初始化： 确认查找规划的开始方位和完毕方位，一般为数组或列表的首尾元素索引。
中心值核算： 核算查找规划的中心方位的索引，即 $mi d = (s t a r t e n d) /2$ 。
比较方针值： 将方针值与中心值进行比较：

假如方针值等于中心值，则查找成功，回来中心值的索引；
假如方针值小于中心值，则更新查找规划为左半部分，行将完毕方位更新为中心值的前一个索引；
假如方针值大于中心值，则更新查找规划为右半部分，行将开始方位更新为中心值的后一个索引。

迭代或递归： 重复上述进程，直到找到方针值或开始方位大于完毕方位为止。

二分查找的时刻复杂度为 O(logn)，其间 n 是待查找规划的巨细。这使得二分查找成为一种高效的查找方法，特别适用于有序数组或列表中的查找操作。

值得留意的是，二分查找要求待查找的数组或列表有必要是有序的。假如待查找的数据量较小，能够挑选简略的线性查找算法，而关于较大的有序数据调集，二分查找一般是更优的挑选。

旅行商问题

旅行商问题（Traveling Salesman Problem，TSP）是一种著名的组合优化问题，它的方针是寻觅一条途径，使得旅行商能够经过一切给定城市一次，然后回到开始城市，而且总路程最短。

旅行商问题一般能够描绘为以下几个要素：

城市调集： 给定一组城市，一般用 N 个点表明，每个点代表一个城市。
间隔矩阵： 关于每对城市 i 和 j，有一个确认的间隔 $d_{ij}$ 表明从城市 i 到城市 j 的间隔。
方针： 旅行商需求从一个开始城市动身，经过一切的城市一次，然后回来开始城市。途径构成一个环路。方针是找到一条途径，使得总路程最短。

旅行商问题是一个组合优化问题，归于NP-hard问题，即没有已知的有用算法能够在多项式时刻内处理一切实例。因而，关于大规划的TSP实例，一般需求选用近似算法或启发式算法进行求解。

一些常用的求解方法包含：

穷举法： 关于小规划的问题，能够运用穷举法来列举一切或许的途径，并核算每条途径的总路程，从中挑选最短的途径。可是跟着城市数量的添加，穷举法的核算量会呈指数添加，变得不可行。
近似算法： 例如最小生成树法、最近邻法等，这些方法虽然不能确保得到最优解，可是在实践运用中一般能够快速给出一个较好的近似解。
启发式算法： 例如模仿退火算法、遗传算法、蚁群算法等，这些方法运用了问题的特定性质，经过迭代优化来寻觅较优解，适用于中等规划的TSP实例。

由于旅行商问题在实践运用中具有广泛的运用价值，因而研究者们一直在探索更高效的求解算法和优化方法，以进步求解功率宽和的质量。

第二章：挑选排序

数组和链表

数组是一段接连的空间，支撑随机拜访。查找简略，添加、删去费事。

链表是一段非接连的空间，只支撑顺序拜访。头部/尾部增删简略，查找费事。

挑选排序

挑选排序：每次从列表中选出最大值/最小值，将其交流到数组的头部。

第三章：递归

递归让程序更容易了解，它没有功能上的优势。实践上，运用循环或许功能更高。

递归包含基线条件和递归条件。

栈结构：先进后出（Last In First Out，LIFO）。

行列：先进先出（First In First Out，FIFO）。

运用递归或许导致调用栈占用很多的内存。处理计划能够是换成循环，也能够是换成尾递归。

第四章：快速排序

欧几里得算法

分治思维（divide and conquer，D&C）：大事化小，小事化了。不断缩小问题的规划。

欧几里得算法：曲折相除法，找最大公约数，处理分土地问题。

快速排序算法

快速排序：挑选基数，将数组分为小于基数，大于基数的左右两块区域，再对左右区域别离进行同样的操作。每次遍历一次数组，能够给基数排好序。均匀时刻复杂度 O(n $lo g$ n)，最坏时刻复杂度 O( $n^2$ )。重复排序时，从头/尾挑选基数就会导致最差状况呈现。随机挑选基数能够避免这一状况。

第五章：散列表

散列函数将输入映射到数字。散列函数的特色：

确认性：关于相同的输入，散列函数总是发生相同的输出。
散列磕碰：散列函数的输入和输出不是唯一对应联系。
不可逆性：散列函数是不可逆的，意味着无法从散列值还原出原始输入数据。
混淆特性：散列函数具有混淆特性，这意味着输入数据的细小变化会导致输出散列值的大幅变化。

散列表的增修改查都只需求常量级的时刻。散列表合适用于：

模仿映射联系。
避免重复
缓存数据

为了避免抵触，需求有：

较低的装载因子（书中写的是填装因子）
杰出的散列函数。

装载因子 = 散列表包含的元素数 / 方位总数。

它反映了散列表的被占用率。装载因子越低，磕碰的概率就越低，由于方位较多。跟着数据的填充，装载因子会不断升高。当装载因子较大时，一般就需求调整散列表的长度来避免磕碰了。一个经验规则是，一旦装载因子大于 0.7，就调整散列表的长度。

在 Java 中，HashMap 的装载因子抵达 0.75 时会进行扩容。（默认容量为 16，也就是说，填充了 12 个元素后会进行一次扩容。）

第六章：广度优先查找（breadth-first search，BFS）

广度优先查找处理两类问题：

途径是否存在
哪条途径最短

有向图：无向图的边是没方向的，即两个相连的极点能够互相抵达。有向图：有向图的边是有方向的，即两个相连的极点，依据边的方向，只能由一个极点通向另一个极点。

能够用行列来完结广度优先查找：

将一切街坊加入行列，从头开始查看。
假如这个元素满意条件，出队，查找完毕。
假如这个元素不满意条件，将其的街坊添加到队尾，持续查找。
需求一个额定的列表查看当时查看的人是否现已查看过。不然或许会呈现循环。

广度优先查找算法的运转时刻：O(V E)，V 为极点数（vertices），E 为边数（edges）

拓扑排序：多个使命之间有依赖联系，对其的排序称为拓扑排序。

拓扑排序是图论中的一个概念，用于有向无环图（Directed Acyclic Graph，DAG）的极点排序。在拓扑排序中，假如图中存在一条从极点 u 到极点 v 的有向边，那么在排序中极点 u 有必要呈现在极点 v 的前面。换句话说，拓扑排序将图中的极点排成一个线性序列，使得关于任意一条有向边 (u, v)，极点 u 在序列中呈现在极点 v 的前面。

拓扑排序可用于启动速度优化，将启动时需求履行的使命列出来，使命间的依赖联系表明出来，进行拓扑排序，然后将能并行的使命并行履行，就能进步启动速度。

拓扑排序演示：www.cs.usfca.edu/~galles/vis…

第七章：狄克斯特拉算法（Dijkstra’s algorithm)

Dijkstra 算法用于找出加权图中前往 X 的最短途径。

广度优先查找能够找出最短途径，但假如每条途径花费的时刻不一样，那么找出最快的途径就能够用 Dijkstra 算法。

Dijkstra 算法进程：

找出最廉价的节点，即可在最短时刻内抵达的节点。
更新该节点的街坊的开支。
重复这个进程，直到图中的每个节点都这样做了。（无需对结尾这样做）
核算终究途径。

由 Dijkstra 算法的进程能够看出，Dijkstra 只适用于有向无环图。

更新街坊开支时，一同记载当时抵达街坊节点的最廉价的方法的前一个节点，能够称之为父节点。终究回溯整条最短途径时，从父节点层层往上即可。

假如价格相同，将价格相同的多个节点都记载下来，回溯时是不是能够找到一切或许的最短途径？

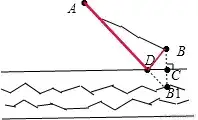
河滨挑水的问题能够用 Dijkstra 算法，或许并不是做对称线的途径最好，或许是经过 C 点最好。由于挑上水之后，桶变重了，之后的途径权重较大。

河滨挑水的问题：从 A 点动身，到河滨挑水到 B 点，走哪条路最好？

Dijkstra 不适用于带负权边的算法，由于负权边或许导致现已处理过的节点又找到一条抵达它的最短途径。

在带负权边的图中，找出最短途径能够用贝尔曼-福德算法（Bellman-Ford algorithm）

模仿，尝试找出 Dijkstra 算法不能用于带环图和带负权边的图的实质原因。

第八章：贪婪算法

每次都取部分最优解，终究获得大局最优解。

有时候，贪婪算法无法获得大局最优解，只能获得一个近似的解。在面对 NP 完全问题（Non-deterministic Polynomial，非确认多项式）时，由于现在没有快速的算法，能够运用贪婪算法获得近似解。

如旅行商问题，是典型的 NP 完全问题。时刻复杂度是 O(n!)，需求核算出一切的解，才能找出答案。

现在没有找到快速辨认 NP 完全问题的方法，一般来讲，涉及“一切组合”的问题一般是 NP 完全问题。

第九章：动态规划

背包问题。每一件物品都能够挑选装或许不装。

cell[i][j] = max(cell[i-1][j], cell[i-1][j-当时重量])

cell[i-1][j] 表明不装此物品，cell[i-1][j-当时重量] 表明装入当时物品。

当问题能够分化为互相独立且离散的子问题时，可运用动态规划。

费曼算法：

将问题写下来。

好好考虑。

将答案写下来。

第十章：K 最近邻算法（k-nearest nerghbours，KNN）

毕达哥拉斯公式：

$sqrt{(x_1-x_2)^2 (y_1-y_2)^2}$

多维空间中的间隔也是类似的。

核算 K 个最近的街坊，能够用来做分类，以此完结电影引荐体系。还能够用来做回归，以此来猜测成果。

余弦类似度：与 KNN 算法不同的是，余弦类似度不核算两个矢量之间的间隔，而是比较他们的视点。合适处理每个人的打分规范不同的场景。

运用 KNN 算法，挑选合适的特征很重要。

KNN 算法可谓进入机器学习范畴的领路人。可用于图画中的文字辨认，思路是阅读很多的图画，将文字的特征提取出来（比方曲线、点、线段），这一步称之为练习。遇到新图画时，提取图画的特征，找出它的最近街坊。

垃圾邮件过滤器运用一种简略的算法——朴素贝叶斯分类器。运用一些数据练习这个分类器，让其知道垃圾邮件中最常呈现的单词、句子（如 million，send me your password）。当收到一封新邮件时，对比其与分类器的类似度，猜测其是否为垃圾邮件。

第十一章：接下来怎么做

树形结构

二叉查找树

为了更方便地运用二分查找，能够在存储数据时就将其存储成「二分」的结构，二叉查找树（binary search tree）应运而生。

平衡二叉树

二叉查找树倾斜时，查询功率不佳，因而，平衡二叉树（Balanced Binary Tree）应运而生。

平衡二叉树是一种通用的概念，它指的是一棵二叉查找树，其间任何节点的左右子树高度差都受到束缚，然后确保树的高度一直坚持在对数级别，然后确保了查找、刺进和删去操作的时刻复杂度为 O(log n)。

AVL 树

平衡二叉查找树的一种完结是 AVL 树，它是一种特殊的自平衡二叉查找树。得名于其发明者G. M. Adelson-Velsky 和 E. M. Landis。它在树的每个节点上维护一个平衡因子（即左子树高度与右子树高度的差），并经过旋转操作来坚持树的平衡。AVL树的特色是关于树中的每个节点，其平衡因子的肯定值不超越1。

红黑树

红黑树也是一种自平衡的二叉查找树，它经过在每个节点上添加一个额定的位来存储节点的色彩（赤色或黑色），而且满意一组红黑树性质，以确保树的高度坚持在对数级别，然后确保了查找、刺进和删去操作的时刻复杂度为 O(log n)。这些性质包含：

每个节点要么是赤色，要么是黑色。
根节点是黑色。
每个叶子节点（NIL节点，即空节点）都是黑色的。
假如一个节点是赤色的，则其两个子节点都是黑色的（即不存在两个相连的赤色节点）。
从任一节点到其每个叶子节点的一切途径都包含相同数量的黑色节点（即，途径中的黑色节点数相等）。

红黑树并不是肯定平衡的，而是经过遵从这些性质来坚持相对平衡。

扩展树（Splay Tree）

扩展树（Splay Tree）是一种自调整的二叉查找树，它经过一系列的旋转操作来调整树的结构，以坚持最近拜访的节点处于树的根方位，然后进步了拜访部分性，而且能够在实践运用中获得较好的功能表现。

扩展树的特色包含：

自调整性： 扩展树在每次拜访或许刺进节点时会对树进行从头平衡，将最近拜访的节点移动到根方位。这样做的好处是，被频频拜访的节点会被置于靠近根的方位，然后进步了对这些节点的拜访速度。
部分性： 扩展树经过频频地进行部分调整，能够将频频拜访的节点调集在一同，构成了部分性，使得对这些节点的拜访更加高效。
简略性： 扩展树的完结相对简略，不需求维护额定的平衡因子或色彩标记等信息，只需经过基本的旋转操作来完结自调整。

虽然扩展树在理论上具有一些长处，可是在实践运用中，它的功能并不总是优于其他平衡树结构，如AVL树或红黑树。这是由于扩展树在最坏状况下或许导致树的高度变得很大，然后影响了其功能。然而，关于特定的运用场景，扩展树仍然或许是一种有用的挑选，尤其是关于需求频频拜访最近拜访节点的状况。

B 树

B树是一种多路查找树，用于处理磁盘I/O功率问题。它具有一个特定的阶（order），其间每个节点能够拥有多于两个子节点。
B树的节点能够容纳很多的键值对，适用于需求频频读写很多数据的场景，如数据库体系中的索引结构。

B 树

B 树是B树的一种变体，与B树比较，它具有更好的查找功能和规划查询功能。
B 树的一切数据都存储在叶子节点上，非叶子节点仅包含键值和指向子节点的指针，这样的规划进步了规划查询的功率。

B*树（B-star tree，读作B星树）

B*树是B树的另一种变体，旨在削减B树割裂的频率，然后进步刺进和删去操作的功能。
与B树比较，B*树答应非叶子节点更少的键值，而且具有更大的节点巨细，以削减树的高度。

反向索引

查找引擎的简略完结：将要害字映射到包含它的网页。当用户查找要害字时，将映射成果呈现给用户。这种数据结构被称为反向索引。

傅里叶变换

傅里叶变换（Fourier Transform）是一种数学东西，用于将一个函数（一般是一个时刻域上的信号）转换成另一个域（频率域）的表明。它是以法国数学家约瑟夫傅里叶的姓名命名的，他在19世纪初提出了这个概念。

傅里叶变换的基本思维是，任何一个周期性信号（甚至是非周期性的信号，经过周期扩展）都能够分化成多个不同频率的正弦和余弦函数的叠加。这些正弦和余弦函数的振幅和相位描绘了原始信号在频率域中的成分。

傅里叶变换有两种常见的方法：接连傅里叶变换（Continuous Fourier Transform，CFT）和离散傅里叶变换（Discrete Fourier Transform，DFT）。

接连傅里叶变换（CFT）适用于接连时刻信号，它将一个接连函数转换为一个接连函数。
离散傅里叶变换（DFT）适用于离散时刻信号，例如在数字信号处理中常见的数字信号。离散傅里叶变换是经过将信号分红离散的时刻点来进行核算的。

傅里叶变换在许多范畴中都有广泛的运用，包含信号处理、图画处理、通讯、音频处理、量子力学等。它能够用来剖析信号的频谱特性，去除噪声，滤波，紧缩数据等。傅里叶变换的逆变换能够将频域表明的信号从头转换回时刻域表明。

简略来说，它能够将一个信号分化成不同频率的成分。

比方，假如你有一段音乐，傅里叶变换能够告知你这段音乐中有哪些频率的声音成分，以及它们的强度（即振幅）和相位（即音调）。这关于了解信号的特征（音乐辨认）、去除噪声、紧缩数据（去掉不重要的音符）等都十分有用。

并行算法

并行算法在处理海量数据时，能够获得一些功能进步。并行算法规划起来很难，要确保他们正确作业并完结希望的速度进步也很难。而且，速度的进步不是线性的，也就是说，两个内核无法把算法速度进步一倍。由于需求考虑并行性管理开支和负载均衡的问题。

以并行快速排序算法为例：（排序并不类似于十月妊娠，即便十个人来也需求十个月才能完结。排序是能够并行的，十个月的使命能够让十个人用一个月完结。）

并行快速排序的基本思维是运用多个处理单元一同处理待排序数据的不同部分，然后进步排序的功率。

一种常见的并行快速排序的完结原理：

区分阶段： 类似于串行版本的快速排序，首要挑选一个基准元素，然后将待排序数据分割成两部分，小于基准元素的部分和大于基准元素的部分。这个进程是并行的，能够由多个处理单元一同处理不同部分的数据。
排序阶段： 区分完结后，每个处理单元别离对其担任的部分进行递归排序。这些排序操作也能够并行履行，每个处理单元独立地对其部分进行快速排序。
兼并阶段： 在一切处理单元都完结了排序后，需求将各个部分兼并起来。这一阶段的完结能够选用串行或许并行的方法，取决于详细的并行框架或算法。

并行快速排序的首要应战之一是怎么有用地区分和兼并数据，以及怎么处理不同处理单元之间的负载平衡问题。一般，各种并行快速排序算法会选用一些技能来处理这些问题，例如动态负载平衡、使命分配策略、部分排序和兼并等。

并行快速排序经过一同运用多个处理单元来加速排序进程，能够在必定程度上进步排序的功率，特别是在大规划数据的排序场景中。并行快速排序的时刻复杂度为 O(n)。

分布式算法

分布式算法是一种规划用于在分布式体系中履行的算法。在分布式体系中，多个核算节点（或许核算机）经过网络相互连接，一起完结核算使命。

MapReduce 是一种盛行的分布式算法。MapReduce算法包含两个首要阶段：Map阶段和Reduce阶段。

Map阶段： 在Map阶段，原始数据集被区分红多个小数据块，每个数据块由一个Map使命处理。Map使命将输入数据块转换成键值对（key-value pairs），并生成一系列中心键值对作为输出。每个中心键值对包含一个键和与之相关联的一个或多个值。Map阶段的输出成果被分区（partitioned）并分发到多个Reduce使命。
Reduce阶段： 在Reduce阶段，一切具有相同键的中心键值对被发送到同一个Reduce使命。Reduce使命对这些数据进行汇总处理，并生成终究的输出成果。一般状况下，每个Reduce使命发生一个输出文件，终究的成果由一切Reduce使命的输出组合而成。

概率型数据结构

布隆过滤器

布隆过滤器是一种特殊的数据结构，用于快速判别一个元素是否存在于一个调会集。它经过运用少数的内存空间和多个哈希函数来完结快速查找，常用于大规划数据的判重和过滤操作。虽然它有必定的误判率，但在需求高效判别很多数据是否存在的场景下，布隆过滤器是一种十分有用的东西。

布隆过滤器的中心思维是经过运用多个哈希函数和一个位数组来表明一个调集，然后完结高效的查找。

布隆过滤器的基本原理如下：

位数组： 布隆过滤器运用一个长度为m的位数组来表明调集，初始时一切位都初始化为0。
多个哈希函数： 布隆过滤器运用多个不同的哈希函数（一般是k个），每个哈希函数能够将调会集的元素映射到位数组中的不同方位。
刺进操作： 当一个元素要被刺进到调会集时，布隆过滤器会对该元素进行k次哈希操作，并将位数组中对应的方位设置为1。
查找操作： 当需求判别一个元素是否存在于调会集时，布隆过滤器同样对该元素进行k次哈希操作，然后查看对应的位数组方位是否都为1。假如有任何一个方位为0，则能够确认该元素必定不在调会集；假如一切方位都为1，则或许存在于调会集，但不是确切的依据。

布隆过滤器的长处是空间功率高和查询功率快，由于它只需求运用少数的内存空间，而且不需求存储实践的元素信息，只需求存储哈希值的方位。可是，布隆过滤器也有必定的缺点，即存在必定的误判率（false positive），即有些元素被判别为存在于调会集，但实践上并不存在。

布隆过滤器在实践运用中常被用于缓存、网页爬取、拦截垃圾邮件、数据过滤等场景，尤其是在需求快速判别一个元素是否归于一个大规划调集的状况下，布隆过滤器能够供给高效的处理计划。

HyperLogLog

HyperLogLog是一种概率型数据结构，用于对大规划数据会集的不重复元素进行近似计数。它的规划旨在供给高效的内存运用和快速的近似计数，适用于大规划数据集的基数（不重复元素的数量）估量。

HyperLogLog的基本原理是运用一个位数组和一组哈希函数来表明输入数据会集的不同元素。每个元素经过哈希函数映射到位数组的某个方位，然后依据哈希值的一部分来确认位数组中相应方位的值。终究，经过对位数组进行一些统计和核算操作，能够估量出数据集的基数。

HyperLogLog的特色包含：

内存功率高： HyperLogLog运用的内存量很小，而且与输入数据规划无关，因而适用于处理大规划数据集。
计数准确性： 虽然HyperLogLog供给的是一种近似估量，但在实践中能够抵达很高的准确度，一般能够抵达小于1%的误差率。
快速核算： HyperLogLog的核算复杂度很低，而且能够经过并行和分布式方法完结高效核算。

HyperLogLog常被用于大规划数据的去重、基数估量、流量剖析等场景。例如，在大数据处理和数据发掘范畴中，能够运用HyperLogLog来快速估量一个数据集的去重后的元素数量，而不必存储一切元素的实践值，然后节约内存和核算资源。

暗码学

SHA 算法

SHA（Secure Hash Algorithm，安全哈希算法）是一系列暗码学哈希函数的宗族，用于生成数据的固定巨细的哈希值，一般表明为40个十六进制数字。SHA算法是由美国国家安大局（NSA）规划，并由美国国家规范与技能研究所（NIST）发布的一系列规范。

SHA算法的首要特色包含：

固定长度输出： SHA算法生成的哈希值具有固定的长度，不受输入数据的长度影响。
单向函数： SHA算法是单向函数，即从哈希值无法推导出原始输入数据。这意味着即便知道哈希值，也无法恢复出原始数据。（用其存储暗码是适当安全的）
唯一性： 不同的输入数据一般会生成不同的哈希值。虽然哈希磕碰（即不同的输入数据生成相同的哈希值）是或许的，但SHA算法规划上尽量避免磕碰的发生。

SHA算法的常见版本包含SHA-1、SHA-256、SHA-384和SHA-512等。它们的差异在于输出的哈希值长度不同，以及运用的轮数和轮函数等细节。

SHA-1 生成的哈希值长度为 160 位（20 字节）。(有漏洞，已不被运用）

SHA-256 生成的哈希值长度为 256 位（32 字节）。

SHA-384 生成的哈希值长度为 384 位（48 字节）。

SHA-512 生成的哈希值长度为 512 位（64 字节）。

SHA算法在信息安全范畴有着广泛的运用，包含数据完整性校验、数字签名、音讯认证等。例如，SHA算法常被用于对暗码学散列进行数字签名、证书验证、SSL/TLS握手等场景中。需求留意的是，由于SHA-1算法存在安全漏洞，因而在许多运用中现已逐渐被更安全的SHA-256等算法所取代。

bcypt 算法

bcrypt是一种暗码哈希函数，一般用于存储用户暗码的安全散列。它运用加盐、多轮哈希等技能来增强暗码的安全性，以避免常见的哈希进犯，如彩虹表进犯。

bcrypt的首要特色包含：

加盐： bcrypt在哈希核算进程中会随机生成一个盐（salt），并将盐与暗码一同作为输入进行哈希核算。盐的引进添加了暗码的复杂度，避免了针对相同暗码的预先核算进犯。
多轮哈希： bcrypt运用多轮哈希函数（一般为12轮以上），使得每个暗码都需求经过屡次哈希核算才能生成终究的哈希值。这添加了破解暗码的难度，即便运用了高功能硬件也难以快速破解。
可配置性： bcrypt答应调整本钱因子（cost factor），以操控哈希核算的复杂度。经过添加本钱因子，能够进一步添加哈希核算的复杂度，然后增强暗码的安全性。
跨渠道性： bcrypt算法的完结一般是跨渠道的，能够在不同的操作体系和编程语言中运用。

由于上述特色，bcrypt被广泛运用于存储用户暗码等安全敏感数据的场景中，如网站用户身份验证、数据库暗码存储等。比较于一些传统的哈希算法（如MD5和SHA-1），bcrypt供给了更高的暗码安全性，能够更有用地避免暗码走漏和哈希进犯。

Diffie-Hellman 算法

Diffie-Hellman算法是一种用于密钥交流的暗码学算法，能够让两个通讯方在不安全的通讯信道上协商出一个同享的密钥，用于加密进一步的通讯内容。这种密钥交流方法是非对称加密的一种，意味着通讯两边运用不同的密钥进行加密宽和密。

Diffie-Hellman算法的基本思维是运用数论中的离散对数问题来完结密钥交流。算法的首要进程如下：

初始化参数： 通讯两边首要一起挑选一个大素数p和一个原根g，这两个参数是揭露的，但通讯两边保密的。一般p是一个很大的素数，g是一个原根（即模p时生成了整个剩下系的数）。
生成公钥： 每个通讯方挑选一个私钥（一般表明为a和b），并运用公共参数p和g生成对应的公钥。核算公钥的方法是：A方核算公钥为 $A=g^a mod p$ ，B方核算公钥为 $B=g^b mod p$ 。
交流公钥： 通讯两边将自己核算得到的公钥发送给对方。
核算同享密钥： 通讯两边运用对方发送过来的公钥以及自己的私钥核算出同享的密钥。比方，A方运用B方的公钥B和自己的私钥a核算同享密钥 $K=B^a mod p$ ，而B方运用A方的公钥A和自己的私钥b核算同享密钥 $K=A^b mod p$ 。由于指数运算的交流性，终究两边核算出来的同享密钥是相同的。

Diffie-Hellman算法的要害点在于，即便经过网络传输的是公钥，但由于离散对数问题的困难性，进犯者无法从公钥中推导出私钥，因而无法核算出同享的密钥，确保了密钥交流的安全性。这种密钥交流方法被广泛运用于安全通讯协议中，如SSL/TLS、SSH等。

RSA 算法

RSA算法的全称是“Rivest-Shamir-Adleman”算法，它是由Ron Rivest、Adi Shamir和Leonard Adleman于1977年一起提出的一种非对称加密算法。RSA算法以这三位作者的姓氏首字母命名。

SA算法是一种非对称加密算法，它根据数论中的大素数分化问题，被广泛用于数据加密和数字签名等安全通讯范畴。

RSA算法的基本原理如下：

密钥生成：

首要，挑选两个不相等的大素数p和q，并核算它们的乘积N（即N = p * q）。
然后，核算欧拉函数(N) = (p-1) * (q-1)。
接着，挑选一个整数e，满意1 < e < (N)，且e与(N)互质（即e和(N)的最大公约数为1）。
终究，核算e的模反元素d，使得(e * d) mod (N) = 1。

加密：

加密时，将明文音讯M转换为整数m，且满意0 ≤ m < N。
然后，运用公钥(e, N)对m进行加密，得到密文c，核算公式为： $c=m^e mod N$ 。

解密：

解密时，运用私钥(d, N)对密文c进行解密，得到原始音讯m，核算公式为： $m=c^d mod N$ 。

RSA算法的安全性根据大数分化的困难性，即在已知N的状况下，要从N中分化出p和q，以便核算出私钥d，是一种困难的数学问题。现在，RSA算法的安全性依赖于大素数的难以分化性，因而在实践中被广泛运用于加密通讯、数字签名、身份认证等场景中。

需求留意的是，跟着核算能力的增强和量子核算机等新技能的呈现，传统的RSA算法或许会面对一些安全性应战，因而研究者们正在积极探索量子安全的替代计划。

线性规划

线性规划（Linear Programming，LP）是一种数学优化方法，用于求解线性束缚条件下的最优解问题。在线性规划中，方针函数和束缚条件都是线性的，因而问题能够被描绘为在多维空间中的一个多面体中寻觅最大（或最小）值的问题。

线性规划问题的解能够经过各种算法求解，包含单纯形法、内点法、对偶法等。线性规划在各种范畴都有广泛的运用，包含生产计划、资源分配、物流优化、金融出资、网络流量操控等。

一切的图算法都能够运用线性规划来完结。线性规划是一个宽泛得多的框架，图问题仅仅其间的一个子集。

Simplex算法是一种用于处理线性规划问题的常用算法，由美国数学家George Dantzig于1947年提出。Simplex算法经过在多维空间中移动然后找到方针函数在束缚条件下的最优解。

后记

《算法图解》用简略易懂的语言和图解的方法介绍了一系列常见的算法和数据结构，是一本合适初学者入门的算法入门书籍，但关于想要深入学习算法的读者来说，或许需求配合其他更深入的参考资料。

《算法图解》读书笔记