博弈论是一门很风趣的学科,本文将以博弈问题《三个枪手》为脉络,从零根底开端介绍博弈论,和咱们一同博弈论是怎么处理实际问题的。期望经过本文,让咱们都能听懂博弈论。
题目:《三个枪手》
三个小伙子同时爱上了一个姑娘,为了决议他们谁能娶这个姑娘,他们决议用枪进行一次决战。A的射中率是30%,B比他好些,射中率是50%,最出色的枪手是C,他从不失误,射中率是100%。由于这个清楚明了的现实,为公平起见,他们决议按这样的次序:A先开枪,B第二,C终究。然后这样循环,直到他们只剩余一个人。那么A榜首枪应该怎样打?谁活下来的概率最大?
****以下是初步评论进程,启发咱们思考:
论证: 每个人的方针都是活下来,为了方针寻觅最好的战略。以下开端分人评论 A: •若A开枪射杀了B,则下个开枪是C,C会100%射杀A,这不是一个好战略 •若A开枪射杀了C,则下一轮B会有50%的几率杀掉自己 •若A开枪未打中,则下一轮能够坐山观虎斗,所以A最好的战略看似是成心打空枪更好一些 B: •若A现已将C射杀,此刻B与A互相射击,B的生计率高于A •B只能挑选射杀C,由于只需C活着,都会优先射杀B C: •先消除要挟大的B,然后再杀掉A,只需自己有开2枪的机会,直接取胜
问题剖析 & 博弈论根底
不得不说,三个枪手在这种你死我亡的死斗中还能严格遵守决战次序,实在是令人钦佩。
接下来,让咱们一同剖析这个问题,并在剖析的进程中介绍一些博弈论概念。
(1)根本特征
咱们持续剖析这个状况,首要需求清晰:这是一场零和博弈, 信任咱们对这个词都不陌生。
在零和博弈中,资源总量是固定的,协作不会产生任何额定收益,任何人的收益都意味着其他人等量的丢失。
在这场决战中,咱们争斗的资源便是这一个胜者的名额,任何一人的成功就必定伴随着其他二人的失败,没有任何共赢的途径。因而这归于典型的零和博弈。
这种“不是你死,便是我活”的零和博弈归于典型的非协作博弈,其典型特点是博弈者需求绝对的利己,由于协作不会共赢的。
同时,这场决战还满足两个条件:
① 每个人都知道其他人的射中率是多少。即,每个参与者都把握了其他参与者的信息。
② 每个人举动有先后次序,且后行者能够观察到先行者所挑选的举动。
这两个条件无妨概括为:“信息透明”和“动态改动”。满足这两个条件,这种博弈被称作彻底信息动态博弈。
(2)要害——纳什均衡
从以上剖析中,咱们得出了这场博弈的三个特征:1️⃣ 绝对利己、2️⃣ 信息透明、3️⃣ 动态改动。总结:
每个人想要取胜,首要需求根据当时形势(由于局势动态改动),并结合对手的信息(由于信息透明),做出对自己最有利的决议计划(由于绝对利己)。
根据以上特征做出假定:不只一切人都会做出自己的最优决议计划,而且他们做出最优决议计划的前提,是假定其他人也会做出最优决议计划。 由于信息透明,既然一切人都知根知底,咱们就都会企图猜测其他人的决议计划,都是高手过招,谁的心眼儿也不比谁的少,谁也不觉得其他人会走一步臭棋。因而,咱们能够以为:每个人都是在“预判”其他人的最优决议计划,并以此为根底做出自己的最优决议计划。
这个假定是回答本问题的要害,只有建立了这个假定,咱们才或许核算出每位枪手的生计概率。否则,这个问题将变得彻底随机,再多的推理都没有含义。试想,假如B、C上来一通乱打,不消除对自己要挟最大的,先共同把枪口对准“小菜鸡”A,那A的生计概率,能够说是几乎没有,核算A的生计概率还有含义吗?
为了便利咱们了解,再举个小栗子:
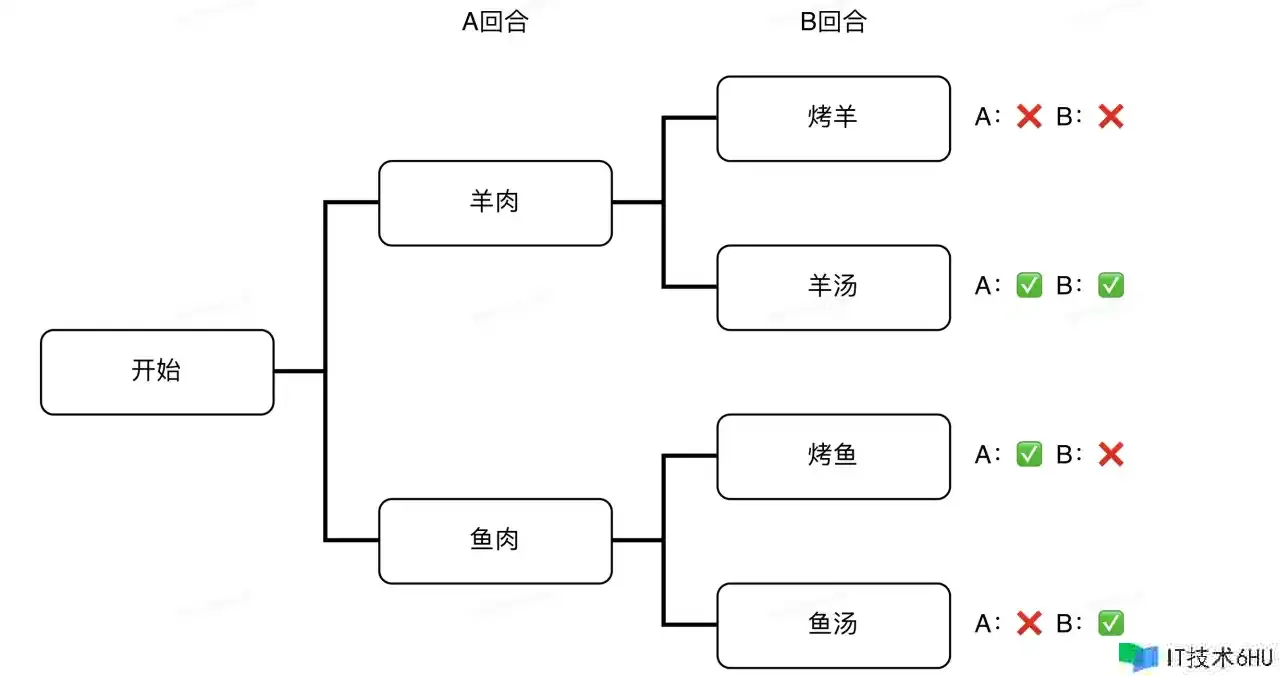
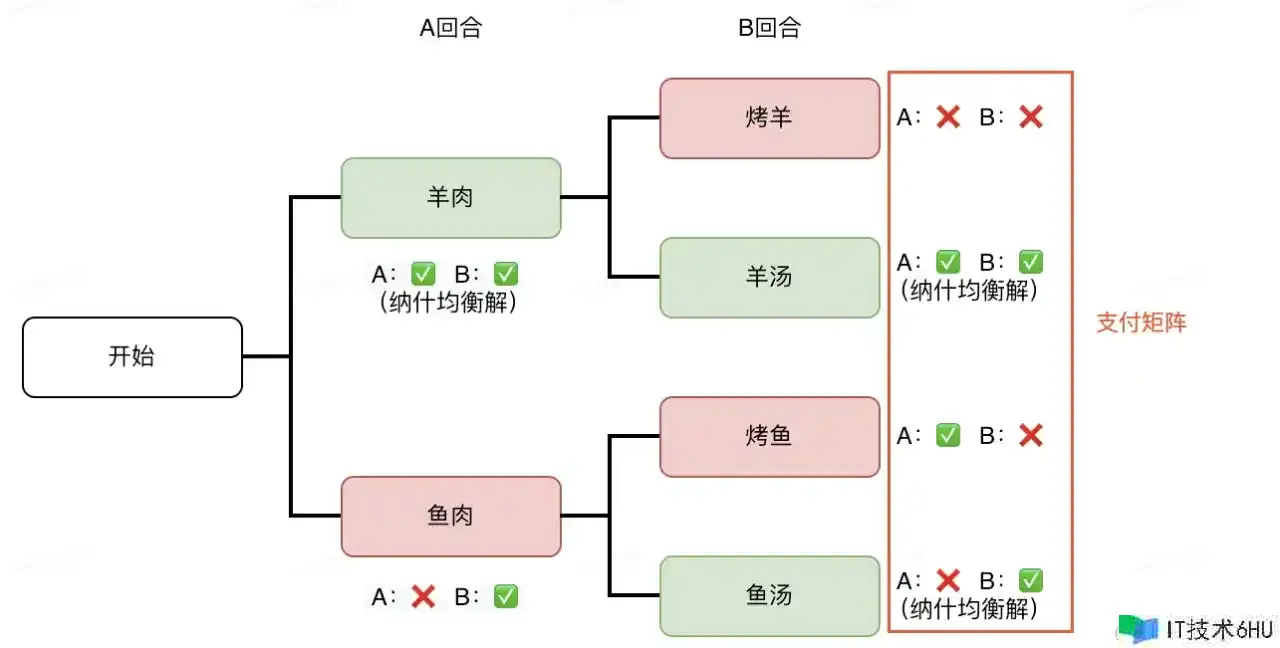
鱼羊问题: A、B二人合伙煮饭,A买肉,B下厨;A能够决议买什么肉,B能够决议怎样做。A能够买到的肉有:羊肉、鱼肉,B会的做法别离是:烤肉、肉汤。A想吃到烤鱼或者羊汤,B只想喝汤。A、B都知道对方的喜好,但都只想满足自己的口味。那么,A应该怎样决议计划才能收益最大? 剖析: 这也是一个彻底信息动态博弈问题:
彻底信息——A、B都清楚对方想吃什么;动态博弈——只有A先买完肉,B才能烹饪。
对于动态博弈问题,最好的剖析东西是博弈树。博弈树的根节点代表博弈的开端,叶子节点代表博弈的终止。咱们能够画出这场博弈的博弈树,如下:
这个博弈树呈现了两次分叉,别离代表了A、B的两次挑选,终究得到了4种成果。聪明的读者们,假如你是A,会怎样选呢?无妨用方才的假定推理:
由于A知道:B挑选做汤对B的收益更高;
所以A假定:B必定会挑选对B收益更高的决议计划——做汤(预判其他人会做出最优决议计划);
所以A推演:假如A选了鱼肉,也得不到烤鱼,只会得到鱼汤;假如A选了羊肉,能够得到羊汤,而羊汤对A的收益更高。
因而,A的最佳决议计划是挑选羊肉。A、B二人终究到达的最佳挑选是羊汤。
在鱼羊问题中,正由于A对B的挑选进行了预判,才让自己得到了最大收益。
当咱们发现,在一场博弈中,一切参与者都做到如此的“机关算尽”,在任何状况下都做出了最优决议计划,让自己得到最大收益。当每个人的收益都无法再持续扩展,这时博弈抵达了一种均衡状况,咱们称这个状况为纳什均衡。 一切参与者的最优战略调集被称为均衡解/均衡点。在纳什均衡状况下,各方的收益/胜率才是或许被核算的。一局博弈也或许存在不止一个纳什均衡解。
咱们能够把博弈看作天平,假如每个博弈者都使出了浑身解数,让成功的天平向自己倾斜,直到任何一方都无法再扩展自己的优势,到达一种“僵持”,那这便是纳什均衡状况。
比方在上面的鱼羊问题中,“羊汤”便是这个博弈的纳什均衡点。在该点,A、B两边均获得了各自的最高收益。
Tips:纳什均衡(Nash Equilibrium)和约翰纳什 纳什均衡是指这样一种战略组合,在该战略组合中,每一个博弈者都信任,在给定竞争对手战略的状况下,他挑选了最优战略。任何一位玩家在此战略组合下,单方面改动自己的战略都不会进步自身的收益。 风趣的是,纳什均衡下所到达的个人最大收益,并不必定能带来整体的最大收益,比方经典的博弈事例“囚徒窘境”,感兴趣的读者能够去看一看。 1950年,纳什均衡由22岁的美国数学家约翰纳什提出,宣布在他27页的博士论文《非协作博弈》中。以“纳什均衡”理论为中心的非协作博弈论一经发布,随即引起轰动,在经济学以及与经济学原理相关的金融、管帐、营销和政治等各个学科都掀起了巨大变革,奠定了现代主流博弈论和经济理论的底子根底。1994年,约翰纳什获得诺贝尔经济学奖。以约翰纳什为原型的电影《美丽心灵》获得了第74届奥斯卡金像奖最佳导演与最佳影片奖。
(3)子博弈的纳什均衡
在动态博弈问题中,博弈会按次序分屡次进行,在整个博弈进程中会呈现若干中心状况,这些状况源于这场博弈,由于博弈还未完毕,因而假如将中心态视为开端,也能够看作一场新的博弈,咱们把这些博弈的中心状况称为子博弈。对应到博弈树中,博弈树的每个非叶子节点都可看作一个子博弈。
怎么了解子博弈: 围棋、象棋等棋类运动是一种典型的动态博弈游戏。整场博弈始于棋局开端,而「残局」就能够视作整场博弈的子博弈。 棋类运动中的纳什均衡: 在棋类运动中,让两边都“不吃亏”的下法也归于纳什均衡。象棋中的“当头炮,把马跳”,围棋中的定式,这种几乎约定俗成的经典下法,使两边都能满足,几乎成为了两边的最优解,其本质便是纳什均衡。
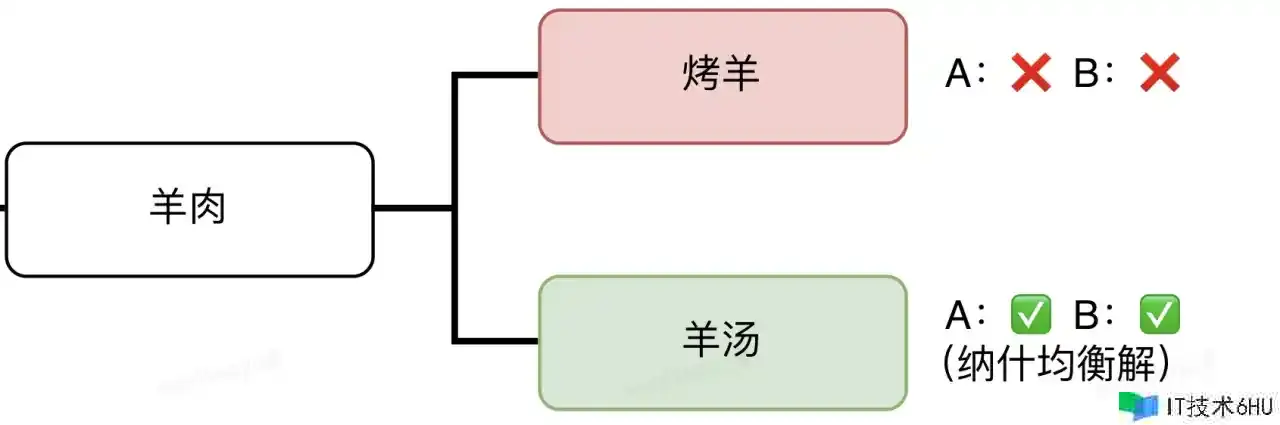
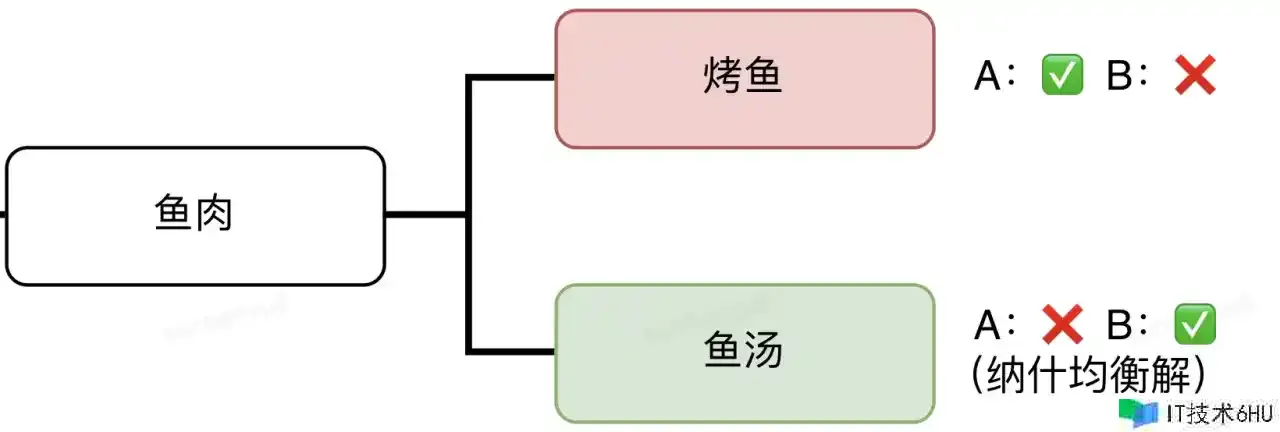
回到上文的鱼羊问题,让咱们再次从子博弈和纳什均衡的视点剖析A的最佳决议计划。当A榜首次做出决议计划后,咱们看看A的两个挑选所形成的两个子博弈:
在“羊肉”分支的子博弈中,“羊汤”决议计划对B的收益更高,B挑选该决议计划收益最大,在这一子博弈中构成纳什均衡;
在“鱼肉”分支的子博弈中,“鱼汤”决议计划对B的收益更高,B挑选该决议计划收益最大,在这一子博弈中构成纳什均衡。
(这两个子博弈是B的回合,所以只需让B的收益最大)
那么,咱们就能够以为:“羊汤”决议计划是“羊肉”子博弈的纳什均衡解;“鱼汤”决议计划是“鱼肉”子博弈的纳什均衡解。
(4)反向概括法
如上面的比如,假如一个子博弈能够确定一个唯一的纳什均衡解,那就意味着这个子博弈拥有一个让博弈者利益最大的最优解,咱们信任,只需博弈者乐意让自己的利益最大,他就必定会做出这个最优挑选。因而在纳什均衡的假定下,咱们能够用这个最优解作为这个子博弈的成果。这正是咱们之前说到的中心准则: “每个人都假定其他人也会做出最优决议计划” 。
根据这个原理,咱们能够用子博弈的最优解来作为子博弈的成果,即:
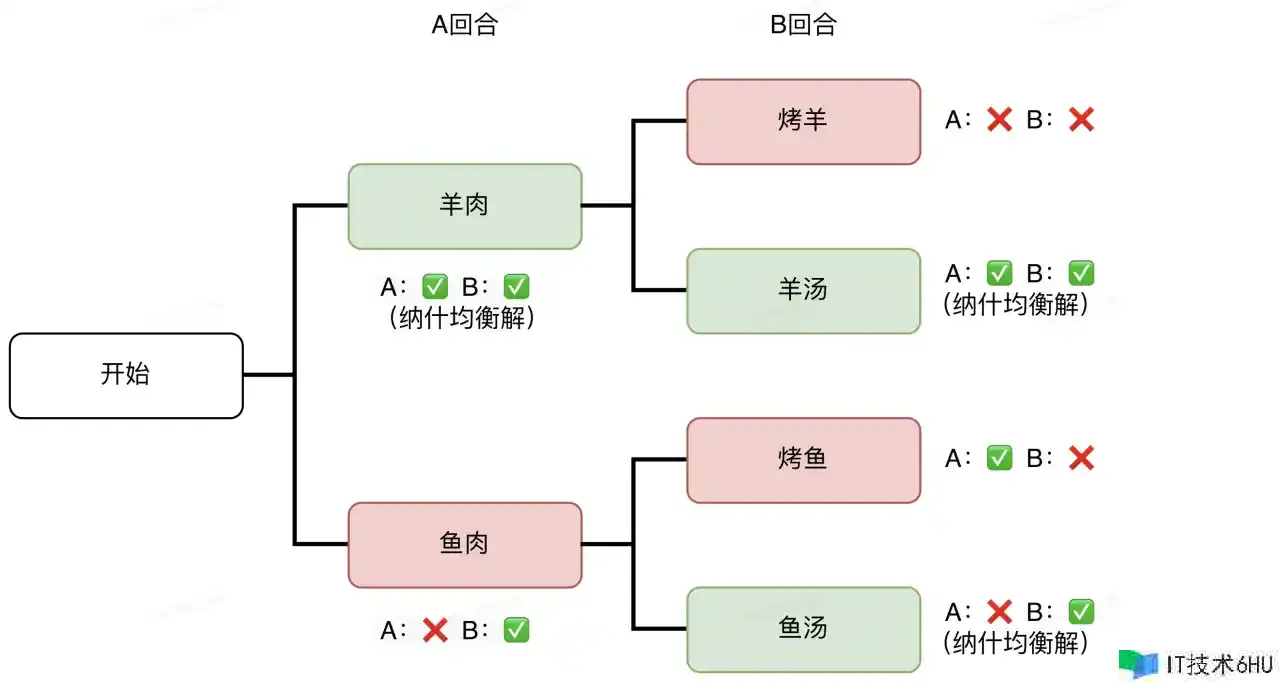
在“羊肉”节点,两边的预期收益为“ A:✅ B:✅”,在“鱼肉”节点,两边的预期收益为“ A:❌ B:✅”。
显然在这二者中,羊肉节点为纳什均衡解,因而A的最佳挑选便是羊肉。与之对应,羊汤便是整场博弈的纳什均衡解。很惋惜,鱼汤虽然是鱼肉子博弈的纳什均衡解,但不是整场博弈的纳什均衡解。 由此,鱼羊问题的整棵博弈树为:
以上,咱们从纳什均衡的视点从头推导了鱼羊问题,这也是求解彻底信息动态博弈问题的根本办法:
从博弈树的一切叶子节点开端,找出一切叶子节点的纳什均衡解,再反向推导回上一层节点,并得出上一层节点的纳什均衡解,直到博弈树根节点,终究得出整场博弈的纳什均衡解。由于终究的纳什均衡解是从子博弈中层层“精炼”而来,整个求解进程被称为子博弈精炼纳什均衡,这个根本办法被称为反向概括法。
简略了解,反向概括法是一种根据成果去反向推理的思维,经过猜测不同决议计划所带来不同成果的好坏,然后挑选最好的决议计划。
问题求解
祝贺你!读到这儿,你现已了解了博弈论的根本概念,并把握了处理博弈问题的根本办法。
接下来让咱们进入正题,试着用反向概括法处理一下「三个枪手」问题。
(1)画博弈树
剖析这类动态博弈问题的榜首步是:画出博弈树。
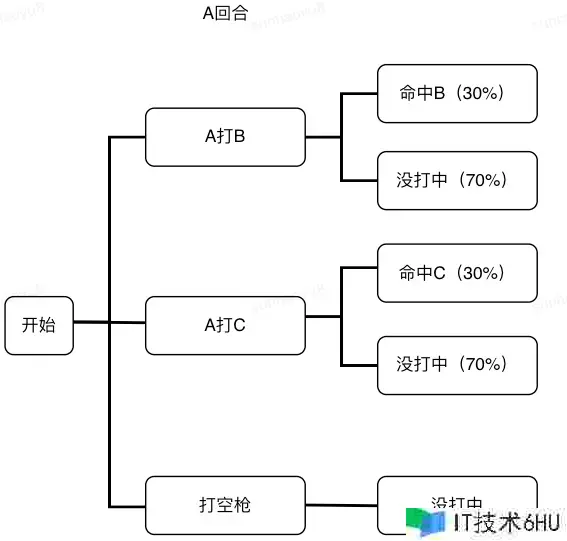
从榜首回合开端,枪法最差的A先开枪,他有三个挑选:打B、打C,还有成心放空枪。
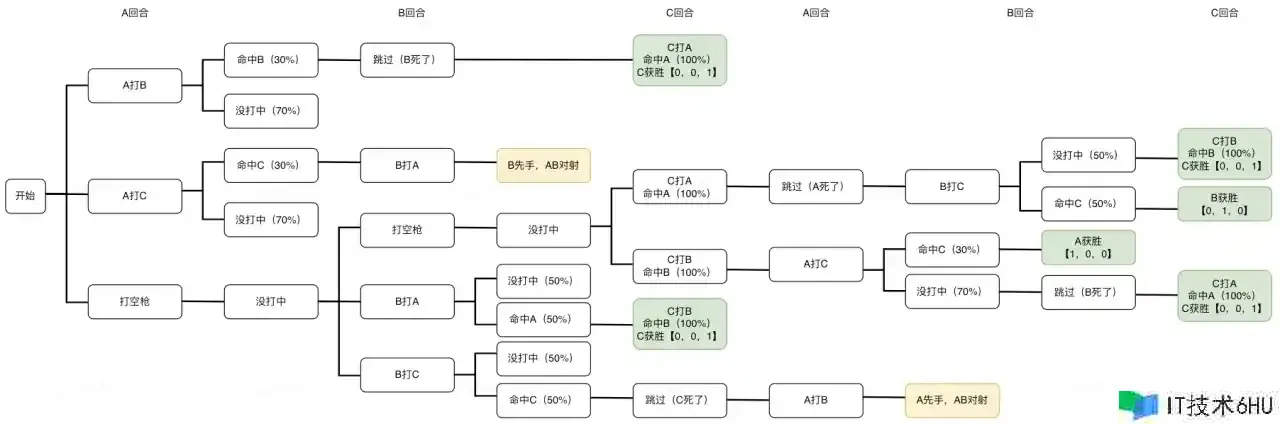
咱们发现,对A而言,状况有点不确定性:当A挑选打B或打C时,成果不确定。由于A只有30%的几率射中,而有70%的概率打不中,且没打中和放空枪的作用是相同的。因而,A的三个挑选只会带来三个或许的成果:射中B、射中C、没打中。咱们画出榜首轮的博弈树,如下图所示:
在上面的博弈树中,每个决议计划都或许导致“没打中”的局势产生,由于它们是一种状况,咱们就只打开一个这类节点。
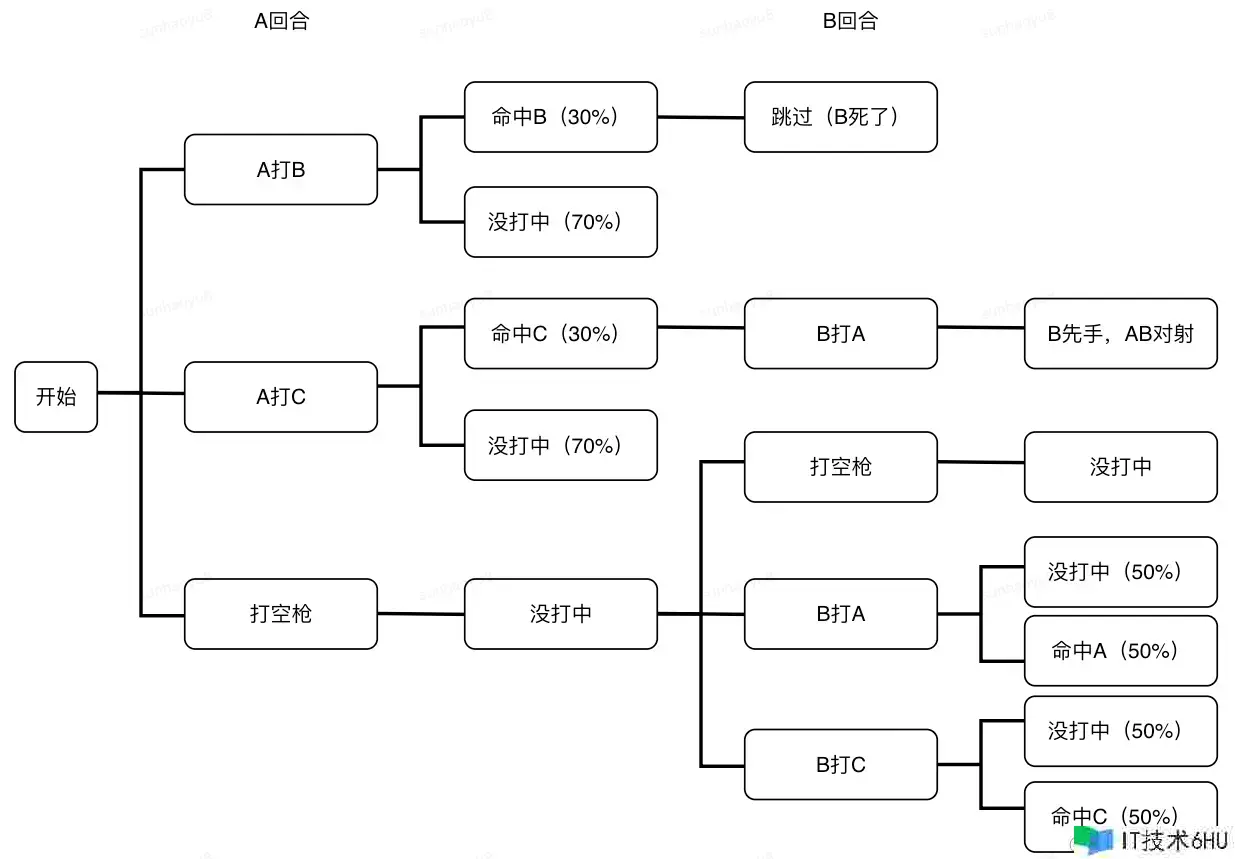
持续按照这个思路打开博弈树,让咱们看看下一回合局势会怎么发展:
如上图所示,到了第二回合,轮到B开枪。这时B会面临三种或许的状况:
(1)假如B现已被A打死了,那就只能惋惜跳过本轮,直接轮到C的回合(如榜首个分支所示);
(2)假如C现已被A打死了,那场上只剩余两个人,二人对射即可(如第二个分支所示)。弥补一句,在只剩两个人时,咱们不考虑放空枪的挑选,这显然没有含义。
(3)假如A没打中,那场上还有三个人,因而此刻B仍有三个挑选:打A、打C和放空枪(如第三个分支所示)。
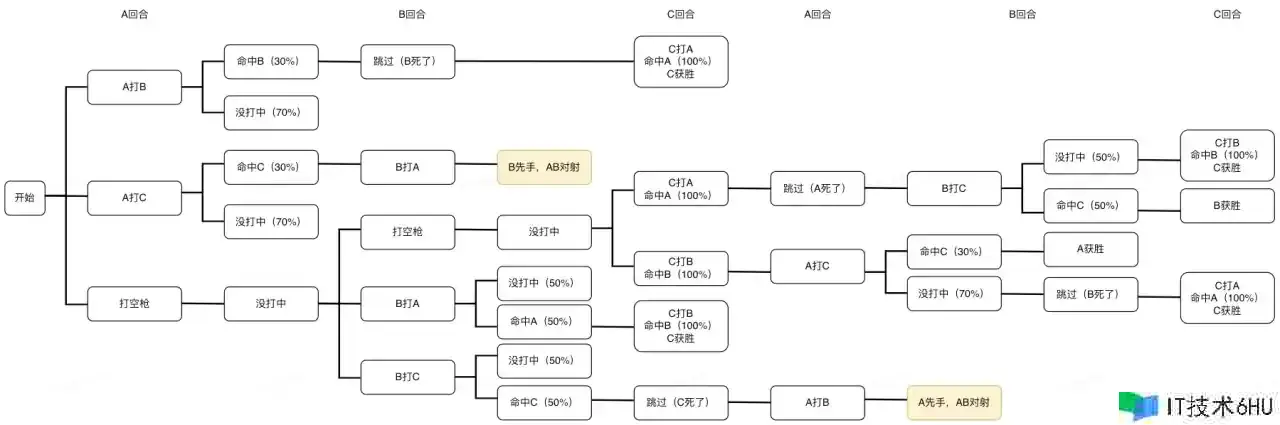
到第三回合,终于轮到弹无虚发的神枪手C进场啦!此处为了简化评论,咱们无妨排除掉C打空枪的选项。原因有二:
(1)打空枪是为了鹬蚌相争,渔翁得利,而C作为全场最强,会被其他人当作最大要挟,显然难以“坐山观虎斗”。
(2)假如C本轮放空枪,博弈局势又将回到起点(轮到A开枪,三人都存活),而只需C开枪,就必定能够筛选一个对手。对C而言,抛弃这一先手机会显然是不明智的。
那么咱们就持续打开博弈树,能够看到:假如本回合场上只剩余两个人,C开枪必定会击杀对手,然后在本轮取得成功;怎么本回合三人都存活,C杀掉一个,还会剩余一个,进入后面的博弈。咱们持续将剩余的状况全部推演完毕。整棵博弈树如下图所示:
能够看到,只需C不死,最快到第三回合,也便是C榜首次开枪时,最迟到第六回合,也便是C第二次开枪时,整场博弈完毕。
有的读者会发现,这棵树上有两个被符号为黄色的节点,没有持续打开,它们是博弈进程中,C首要被筛选后呈现的特殊状况,我将它们称为【B先手,AB对射】和【A先手,AB对射】。咱们按下不表,稍后咱们详细评论这两种状况。
(2)求付出矩阵
画出了博弈树,第二部是求每个叶子节点的付出矩阵。什么叫**「付出矩阵」?这个名词其实有点难明,咱们换个叫法,它又被称为「收益矩阵」,用来描绘每位博弈者在当时节点下的收益状况**。这样是不是好了解多了。举个比如,还记得咱们的老朋友——鱼羊问题吗?最右边的一列,别离表示这个菜肴是否满足了A、B二人的胃口,它便是付出矩阵。
为什么要求付出矩阵呢?由于付出矩阵便是对当时博弈的判别,反映出当时景象对谁更有利,对谁更晦气,这样才能便利做出最优挑选。
回到枪手问题中,怎么衡量每个人的收益?这是一个零和博弈,一切人寻求的便是成为终究的生还者,那么「胜率」就成为衡量收益的标杆。求叶子节点的“胜率矩阵”也很简略,谁赢了,他的胜率便是1,败者是0。
咱们用【A,B,C】的次序,别离代表三个枪手的胜率,例如C取胜,对应付出矩阵便是【0,0,1】。咱们将付出矩阵标注到博弈树的一切叶子节点上,如图中一切绿色的节点:
(3)反向概括
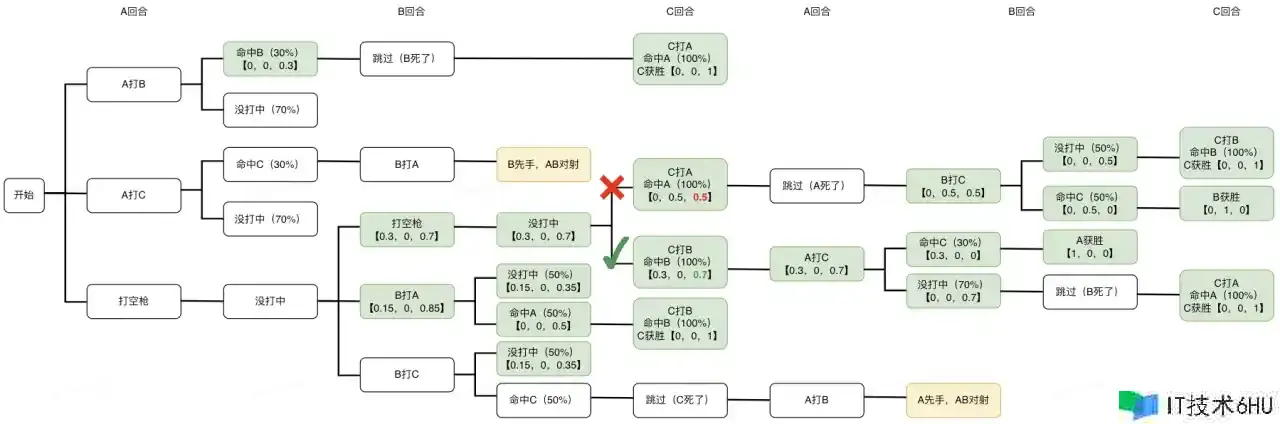
在上面的两步中,咱们现已画出了博弈树,并求出了叶子节点的付出矩阵。前两步都是准备工作,接下来便是第三步,也是求解进程中最中心的逻辑:反向概括法。在这个博弈中,有几个需求提示的规矩:
(1)概率问题:当一个挑选或许有多个成果时,这个挑选的付出矩阵是多个成果的付出矩阵的加权平均。如B挑选打C,射中率是50%,假如射中后的付出矩阵是【0,1,0】,未射中的付出矩阵是【0,0,1】,那么,这个挑选的付出矩阵便是【0,1,0】* 50% 【0,0,1】* 50% = 【0,0.5,0.5】。也便是说,这个挑选有50%的概率B取胜,有50%的概率C取胜。
(2)最优挑选:当一个人面临多个挑选时,他必定会从每个挑选的付出矩阵中,挑选他自己胜率最高的那个。这也便是他这个子博弈的纳什均衡解。
咱们能够用上面两个提示,试着反向推导一下博弈树,看看咱们得到的成果是否共同:
以上是用叶子节点反向概括后得到的博弈树,一切现已求出付出矩阵的节点被符号为了绿色。咱们注意到,在图中呈现了一个“❌”和一个“✅”,这代表一次分支挑选,被符号“✅”的分支是被选中的纳什均衡解,被符号“❌”的分支则是被筛选的分支。
让咱们看看这次挑选:这个子博弈呈现在第三回合,此刻轮到C开枪,A、B都存活,C需求挑选打A仍是打B。从图中不难看出,C假如挑选打A,自己的胜率是0.5,假如挑选打B,自己的胜率会提升到0.7,由于他先处理了更强的对手。因而C必定会挑选后者,那么这个子博弈的付出矩阵,就取这个纳什均衡解的付出矩阵。
(4)「菜鸡互啄」问题
当问题推导到这儿时,咱们发现无法进行下去了——由于咱们前面还留了两个节点没有打开,无法求付出矩阵。那就让咱们看看怎么处理这两个节点吧。
这两个子博弈是在博弈进程中,C首要被筛选后呈现的特殊状况,别离是【B先手,AB对射】和【A先手,AB对射】。此刻,由于场上只剩余A、B,因而二人的射击方针只有对方,但由于A、B二人都不能确保弹无虚发,因而射不到对方的状况理论上永远存在(一般这种状况被称作:菜鸡互啄),假如无限推演下去,博弈树只会堕入死循环,由于没有出口。这下该怎么核算两边的胜率呢?让咱们以【A先手,AB对射】为例,先剖析一下每轮状况。
设A的射中率为a,B的射中率为b,A先手,则每轮产生的状况的概率如下:
| 回合一:A | 回合二:B | 回合三:A | 回合四:B | … | |
|---|---|---|---|---|---|
| 射中的概率 | a | (1-a)b | (1-a)(1-b)a | (1-a)(1-b)(1-a)b | … |
| 未射中概率 | 1-a | (1-a)(1-b) | (1-a)(1-b)(1-a) | (1-a)(1-b)(1-a)(1-b) | … |
上表是怎样算出来的?二者只需有一方射中,游戏即会完毕。假如未射中,则在本轮未射中概率的根底上,别离乘以下个人的射中率,就会别离得到下轮的射中概率和未射中概率:
怎么核算A的胜率?A的胜率,即为A每回合射中的概率之和,即:
是不是看起来很眼熟?你没有猜错,咱们需求使用微积分了(死去的微积分忽然攻击我)。友谊建议:看到数学就头大的读者请自行跳过这部分。
上面的式子能够表示为:
咱们能够发现,这是一个幂级数求和问题。假如还没太看清,咱们令
,则原式变为:
咱们先判别敛散性:由于
,则,那么。
因幂级数
的收敛域是,因而该幂级数收敛。
根据公式
,可得:
这样,咱们就得到了A先手,A、B对射时A的胜率。咱们知道A的射中率为30%,B的射中率是50%,咱们将
,带入可得:。相应地,此刻B的胜率.
同样的公式,当转换为B先手,A、B对射时,
将,代入,可得:,。
(5)得出答案
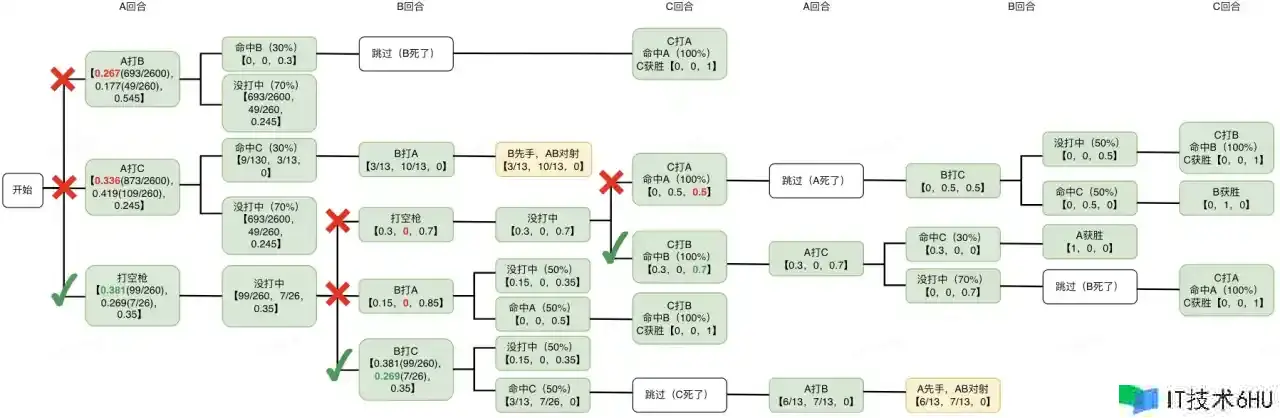
有了上一步核算出来的两个特殊子博弈中A、B的胜率,咱们能够得出:
【A先手,AB对射】的付出矩阵是【6/13,7/13,0】。
【B先手,AB对射】的付出矩阵是【3/13,10/13,0】。
持续完善博弈树,并完结后续的反向概括进程,终究得到的成果是:
咱们经过反向概括法得到了A榜首回合的三个挑选的付出矩阵,比较三种挑选下A的胜率:
A打B——26.7%;A打C——33.6%;打空枪——38.1%,因而咱们终于能够得出这个问题的答案:A的最优战略是打空枪,生计概率是38.1%(99/260).
这个答案同样也论证了咱们一开端的预期——A最好的战略看似是成心打空枪更好一些。风趣的是,这场博弈中,A、B、C的胜率别离为38.1%、26.9%和35%(纳什均衡状况下),看来枪法最差的A生计下来的概率果然也是最高的呢!当然,个人以为,他之所以能拥有最高胜率,首要仍是由于他能够先手啦。
以上,咱们就给出了「三个枪手」动态博弈问题的处理方案,期望经过以上回答,带咱们搞懂博弈论的根本原理。想必必定有读者有疑问:太麻烦了,莫非每次都要画一遍博弈树,手动推演一遍不成?别着急,我将给出以上问题的代码实现,请看下回分解。
扫一扫,与作者技术交流一下吧