1. 图画的卷积

1.1 卷积

卷积是一种数学运算，它将两个函数（或矩阵）结合起来，生成一个第三个函数。在图画处理中，卷积一般用于将一个滤波器与图画进行运算。

图画的滤波器是一种用于增强或按捺图画中特定特征的工具。它一般是一个小矩阵，定义了怎么对图画中的像素进行操作。

卷积在图画处理中有许多应用，包含图画滑润、图画锐化、边际检测和图画切割。

1.2 卷积的原理

在泛函分析中，卷积（convolution），或译为叠积、褶积或旋积，是透过两个函数 f 和 g 生成第三个函数的一种数学算子，表征函数 f 与经过翻转和平移的 g 的乘积函数所围成的曲边梯形的面积。

卷积可分为一维卷积、二维卷积、三维卷积和多维卷积等。

1.2.1 一维卷积

一维卷积在数学上的定义: f 和 g 是实数 R 上的两个可积函数，咱们称（f*g)(n) 为 f、g 的卷积。

其连续的定义为：

$int_{-infty}^{infty} f(tau)g(n-tau)dtau$

其离散的定义为：

$sum_{tau=-infty}^{infty}f(tau)g(n-tau)$

1.2.2 二维卷积

在图画处理中，咱们常用的是二维卷积。其原理是将一个称为卷积核(滤波器)的矩阵与图画进行滑动运算，然后得到一个新的图画。

滑动运算是指将卷积核在图画上逐一像素移动，并对每个方位进行卷积操作。

在图画的二维卷积中，如果把图画矩阵简写为 I 把卷积核 Kernal 简写为 K，则目标图画的第 (i,j) 个像素的卷积值为：

$sum_{m}displaystyle sum_{n} I(m,n)K(i-m,j-n)$

其间，I 是一个二维矩阵，K 是一个大小为 mxn 的卷积核。基于卷积的可交换性，能够把上述公式改成：

$sum_{m}displaystyle sum_{n} I(i-m,j-n)K(m,n)$

与之类似的还有互相关函数(corresponding function):

$sum_{m}displaystyle sum_{n} I(i+m,j+n)K(m,n)$

它在许多图画处理库和深度学习库中，经常会用到。

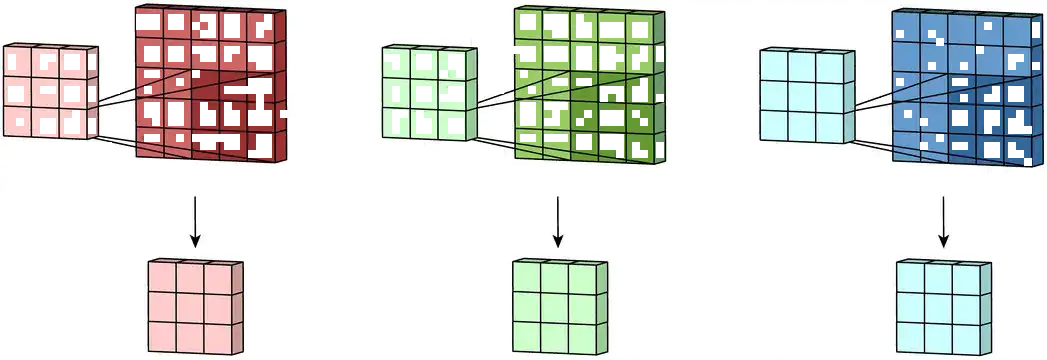
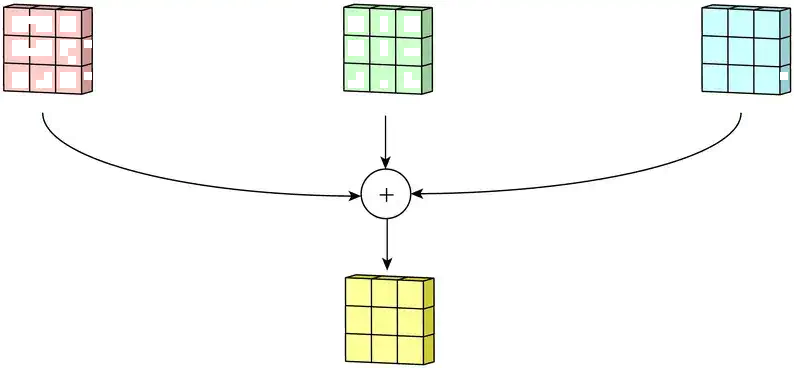
上图实质上是二维单通道的卷积，关于二维多通道的卷积如下图所示，将每个卷积核应用到每一个通道上。

然后将每个通道处理后的每个加在一起以形成单个输出通道。

1.2.3 三维卷积

三维卷积是卷积在三维空间上的推行。它将一个三维的滤波器与一个三维的输入数据进行卷积运算，得到一个三维的输出数据，以提取三维数据中的特征。主流的深度学习结构，都供给了三维卷积的完成。

1.3 卷积的性质

卷积具有交换律、结合律、分配律，以二维卷积为例它具有以下的性质：

交换律：f(x, y) * g(x, y) = g(x, y) * f(x, y)
结合律：(f(x, y) * g(x, y))* h(x, y) = f(x, y) * (g(x, y) * h(x, y))
分配律：f(x, y) * (g(x, y) + h(x, y)) = f(x, y) * g(x, y) + f(x, y) * h(x, y)

2. 图画滤波

2.1 图画滤波

图画滤波是一种图画处理技能，用于增强或按捺图画中的特定特征，它能够看作是卷积的一种特殊情况。图画滤波能够用图画卷积来完成，但是图画卷积不一定是图画滤波。

在 OpenCV 中，供给了丰富的图画滤波函数，能够满足各种图画处理需求。常用图画滤波函数包含：

均值滤波: blur()、boxFilter()
高斯滤波: GaussianBlur()
中值滤波: medianBlur()
双方滤波: bilateralFilter()
非线性滤波: fastNlMeansDenoising()
边际检测滤波: Sobel()、Scharr()、Laplacian()
形态学滤波: erode()、dilate()、morphologyEx()
频域滤波: dft()、idft()

下面的例子，别离展现了原图经过均值滤波、高斯滤波、中值滤波和双方滤波之后的作用图。特别是双方滤波，对原图中的美人进行了美颜和磨皮。

#include <opencv2/opencv.hpp>
#include <opencv2/core.hpp>
#include <opencv2/highgui.hpp>
#include <opencv2/imgproc.hpp>
using namespace std;
using namespace cv;
int main() {
    Mat src = imread(".../girl.jpg");
    // 均值滤波
    Mat blurred_image;
    blur(src, blurred_image, Size(15, 15));
    // 高斯滤波
    Mat gaussian_blurred_image;
    GaussianBlur(src,gaussian_blurred_image, Size(15, 15), 0);
    // 中值滤波
    Mat median_blurred_image;
    medianBlur(src, median_blurred_image,15);
    // 双方滤波
    Mat bilateral_filtered_image;
    bilateralFilter(src, bilateral_filtered_image,15, 80, 80);
    imshow("Original Image", src);
    imshow("Blurred Image", blurred_image);
    imshow("Gaussian Blurred Image", gaussian_blurred_image);
    imshow("Median Blurred Image", median_blurred_image);
    imshow("Bilateral Filtered Image", bilateral_filtered_image);
    waitKey(0);
    return 0;
}

OpenCV 还供给了自定义的滤波器 filter2D() 函数，在该系列的第九篇文章中，从前介绍过 filter2D() 函数。

下面的例子，展现了运用 filter2D() 函数对图画进行模糊和锐化。

#include <opencv2/opencv.hpp>
#include <opencv2/core.hpp>
#include <opencv2/highgui.hpp>
#include <opencv2/imgproc.hpp>
using namespace std;
using namespace cv;
int main() {
    Mat src = imread(".../girl.jpg");
    imshow("src", src);
    Mat blurred_image,sharpen_image;
    Mat kernel1 = Mat::ones(5, 5, CV_32F) / (float)(25);
    Mat kernel2 = (Mat_<char>(3, 3) << 0, -1, 0, -1, 5, -1, 0, -1, 0);
    filter2D(src, blurred_image, -1, kernel1);
    filter2D(src, sharpen_image, -1, kernel2);
    imshow("Blurred Image", blurred_image);
    imshow("Sharpen Image", sharpen_image);
    waitKey(0);
    return 0;
}

下面简单解释一下 filter2D() 函数：

void filter2D( InputArray src, OutputArray dst, int ddepth,
                            InputArray kernel, Point anchor = Point(-1,-1),
                            double delta = 0, int borderType = BORDER_DEFAULT );

第三个参数 ddepth: 输出图画的深度。当 ddepth 输入值为 -1 时，目标图画和原图画深度坚持一致。

第四个参数 kernel: 卷积核。

第五个参数 anchor: 卷积核的锚点。

第六个参数 delta: 卷积结果与原图画相加的值。

第七个参数 borderType: 鸿沟处理方法。

2.2 图画滤波的分类

依据滤波器在图画域和频域的操作方法，图画滤波能够分为空间域滤波和频域滤波。

2.2.1 空间域滤波

空间域滤波直接对图画中的像素进行操作，依据滤波器与图画像素之间的空间联系来计算输出像素的值。空间域滤波的计算量一般较小，但滤波作用往往比较局限。

空间域滤波按滤波器的线性特性又可分为：

线性滤波：滤波器输出与输入之间呈线性联系。

常用的线性滤波器包含：

a 均值滤波：用于去除图画噪声，具有滑润图画的作用。

b 高斯滤波：具有滑润图画和边际坚持的作用。

c 中值滤波：具有去除椒盐噪声和坚持边际细节的作用。

d 拉普拉斯滤波：用于边际检测。
非线性滤波：滤波器输出与输入之间不呈线性联系。

常用的非线性滤波器包含：

a 中值滤波：用于去除椒盐噪声和坚持边际细节。

b 双方滤波：具有滑润图画和坚持边际细节的作用。

c 自适应滤波：依据图画部分特性进行滤波，具有较好的滤波作用。

2.2.2 频域滤波

频域滤波是将图画傅里叶变换到频域，然后对频谱进行滤波，最后再将频谱逆傅里叶变换回空间域得到滤波后的图画。频域滤波的计算量一般较大，但滤波作用往往比较灵活。

频域滤波按滤波器的作用方法又可分为：

低通滤波：滤除图画中的高频成分，具有滑润图画的作用。
高通滤波：滤除图画中的低频成分，具有锐化图画的作用。
带通滤波：滤除图画中的特定频段成分，具有增强图画纹理的作用。

3. 总结

图画卷积和图画滤波是图画处理中两个密切相关的概念。它们都涉及到运用滤波器对图画进行操作，以取得新的图画。

图画卷积是图画滤波的基础，图画滤波能够经过图画卷积来完成，但图画滤波也能够运用其他方法来完成。

图画卷积和图画滤波具有广泛的应用，经过运用不同的滤波器，能够完成各种图画处理作用。

OpenCV 笔记(27)：图像的卷积与滤波

1. 图画的卷积

1.1 卷积

1.2 卷积的原理

1.2.1 一维卷积

1.2.2 二维卷积

1.2.3 三维卷积

1.3 卷积的性质

2. 图画滤波

2.1 图画滤波

2.2 图画滤波的分类

2.2.1 空间域滤波

2.2.2 频域滤波

3. 总结

作者信息

OpenCV 笔记(27)：图像的卷积与滤波

1. 图画的卷积

1.1 卷积

1.2 卷积的原理

1.2.1 一维卷积

1.2.2 二维卷积

1.2.3 三维卷积

1.3 卷积的性质

2. 图画滤波

2.1 图画滤波

2.2 图画滤波的分类

2.2.1 空间域滤波

2.2.2 频域滤波

3. 总结

相关文章

MATLAB神经网络工具箱Neural Net Fitting操作方法

HashMap的实现原理详解(看这篇就够了)

从扫码登录的原理分析QQ大量被盗事件

一桩Lombok插件引发的故障|带你学会Lombok的安装和使用

作者信息