当时在货拉拉进行的许多AB试验中,存在部分针对细分场景或是分流粒度较粗的战略点评,这些试验中试验单元少,简略随机分流会导致试验与对照的试验前误差(Pre-Experiment Bias)大。
本文档调研了业界先进的试验前误差应对技能(AA回溯、最优随机种子和方差减缩)后,在最优随机分组的基础上,进一步提出了离线分流——用户或司机在试验中的行为与试验前有相关性,能够运用历史数据,将试验方针分为差异很小的两组或多组,以进步AB试验的可靠性和干涉效应点评的准确性。
1. 试验前误差
微软在Edge浏览器的一个AB试验中,改变了一些数据的存储格式,估计不会对用户产生影响。但试验数据显现关键用户参加度方针下降,p 值为0.01,且没有其他侧面方针能够解释这种方针变化。
这类问题通常会被解释为“数据波动”,认为这个明显的试验结果是假阳性(False Positive)。常见的解决计划是重开一次试验,但在实践中,未必有机会重开试验,即便能够重开也会花费额定时刻,拖慢战略或产品功能的上线进度。
微软发现历史数据能够有效地发现和应对试验前差异(Pre-Experiment Bias),进步AB试验的可信度。下文会简略介绍微软在其试验渠道落地的三种技能:AA回溯、最优随机分组和方差减缩。
1. AA回溯(Retrospective-AA Analysis)
在试验进行或结束后,核算和查看在试验前某段时刻内试验组和对照组的方针差异,假如确实在AA回溯中观察到两个组之间的方针存在较大差异,则试验期间方针的差异更有或许是随机化引进的误差。
2. 最优随机分组(SeedFinder)
尽管试验后AA回溯能够辨认试验结果的假阳性,但它有滞后性,在试验开始后才能知道是否存在试验前误差。运用SeedFinder能够在试验前判别出试验和对照组是否存在差异。
在AB试验中,通常运用哈希函数和随机种子将用户随机分配到试验组和对照组。在试验开始前,运用很多不同的随机种子,生成很多试验方针分组计划,并核算其中各组的中心方针的差异,然后挑选一个最佳(差异最小) 的种子用于AB试验。
微软主张生成数百个种子,但最合适的数量会因挑选的产品和方针而异。屡次随机削减了与战略无关的噪声,并进步了试验作用测算的精度。
微软主张结合运用一切三种技能来进步试验结果的可信度。运用SeedFinder找到使试验前中心方针差异最小的随机分组,方差减缩能够进步方针的敏感性(更容易明显)并削减试验前差异,而AA回溯能够查看未经SeedFinder优化过的非必须方针的试验前差异。
本文在SeedFinder的基础上,结合货拉拉AB试验的实践运用场景(如定价、营销),提出了更通用的离线分流的概念。
2. 离线分流
1. 思路
方针:找到两组或多组同质的分群支撑AB试验
解法:试验期间的用户/司机行为和其历史行为有相关性,在此基础上经过随机查找或运筹优化的方法找到历史上差异最小的两组或多组
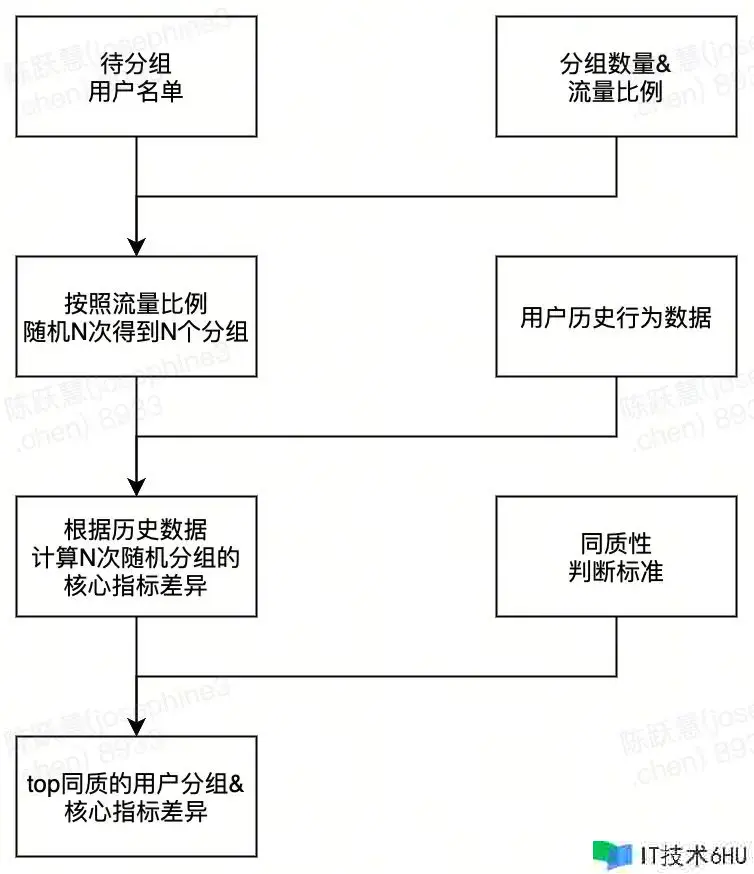
2. 流程图——以用户分流为例
以user_id分流和随机查找为例,同样也能够拓展到司机、空间分流
3. 操作流程
STEP 1 确认试验方针名单
依据实践事务场景,思考试验方针是否满意SUTVA假定(个别处理稳定性假定),例如试验方针是否存在Network Effect / Spillover Effect等,然后挑选合适的试验分流单元(支撑用户、司机、空间)。
依据AB试验需求点评的效应,按照与事务方达到共同的试验单元圈选逻辑,确认待分组试验单元名单。
STEP 2 确认分流相关参数
分组数量:将待分组试验方针名单分为几组
流量份额:子分组试验单元数量占整体试验单元数量的份额;如“对照(40%)、试验组A(30%)、试验组B(30%)”
中心方针:试验设计中关注的中心方针名称;如每个用户曩昔7天的完单量、完单流水等
历史数据切开:圈选练习日期、测验日期(可选,默许与练习日期共同)
同质性判别规范:怎么判别随机出的分组在中心方针上有无差异;如近7天试验组和对照组的人均完单GTV无明显差异(阈值取0.05)或相对差异<1%
随机种子规模:确认需求测验的随机种子的个数和规模
时空片轮播次序(仅适用于时空分流):替换轮播(每天时刻片奇数) 或 替换轮播 隔天回转(每天时刻片偶数)
STEP 3 生成试验方针分流计划
随机查找(Random Search)
运用不同的随机种子,运用与AB渠道完全相同的哈希算法,依据STEP 2中输入的分流参数,生成多个试验方针分流计划
依据同质性判别规范,运用练习日期数据,核算每个试验方针分流计划中两个或多个组之间中心方针的差异和明显性水平,并判别是否同质。 假如满意同质性规范,则保留该试验方针分流计划及同质性点评结果,供后续环节运用
运筹优化
相较于随机查找,运筹优化能够找到最优解,或者在相同的时刻内找到更优解。
输入离线分组对应的参数:
- 同质性要求: 如最小化试验和对照组某段周期(或每周、每天)的各个方针汇总差异
- 方针数量II:如I=2代表2个方针
- 时刻片粒度和数量TT:如时刻片粒度为天,T=7,代表试验和对照组一周内每天的方针类似
- 分组数量KK:如K=2,将待分组试验方针名单分为均等的2组
- 整体数据Xbar{X}:练习集的优化方针,是一个ITKI times T times K的矩阵;假定要把完单总量为500单的100个用户分为两组,我们期望两组的用户的人数和人均单持平,其实是要求两组的人数挨近50且每组人均完单挨近500 / 100 = 5,因而优化的方针应该是和整体类似
- 练习集分组数据XGX^G:XGX^G是一个ITKI times T times K的矩阵,对应着不同试验分组每个时刻点每个方针的值;依据试验方针分流计划,核算各组的方针数据,支撑遗传算法迭代
- 损失函数L(XG,X)L(X^G, bar{X}):依据练习集分组数据XGX^G和整体数据Xbar{X},核算两组或多组的中心方针差异;如MSE
运用遗传算法:
运用遗传算法,求解G∗=argminG∑i=1I∑t=1T∑k=1KL(XG,X)G^* = arg min_G sum_{i=1}^{I} sum_{t=1}^{T} sum_{k=1}^{K}L(X^G, bar{X})
-
假如运用最简略的MSE损失函数,上述数据问题变为:
G∗=argminG∑i=1I∑t=1T∑k=1K(xitkG−xitk)2G^* = arg min_G sum_{i=1}^{I} sum_{t=1}^{T} sum_{k=1}^{K} (x^G_{itk} – bar{x}_{itk})^2
-
假如考虑的多个方针的标准不同,可运用normalizaiton,如:
G∗=argminG∑i=1I∑t=1T∑k=1K(xitkG−xitkxitk)2G^* = arg min_G sum_{i=1}^{I} sum_{t=1}^{T} sum_{k=1}^{K} (frac{x^G_{itk} – bar{x}_{itk}}{bar{x}_{itk}})^2
-
假如方针中存在一些离群点,也能够运用更Robust的损失函数,如Huber loss
运筹优化履行举例:
| 城市分群 | 方针名称 | 日期 | |||
|---|---|---|---|---|---|
| 2022/7/1 | 2022/7/2 | 2022/7/3 | 2022/7/4 | ||
| 核算整体&优化方针 | |||||
| 整体 | 履行单量 | 1,000,000 | 1,200,000 | 1,100,000 | 900,000 |
| 配对单量 | 850,000 | 1,020,000 | 935,000 | 765,000 | |
| 每组方针(均分为2组) | 履行单量 | 500,000 | 600,000 | 550,000 | 450,000 |
| 配对单量 | 425,000 | 510,000 | 467,500 | 382,500 | |
| 生成城市分群 | |||||
| 城市组1 | 履行单量 | 498,000 | 598,000 | 548,000 | 448,000 |
| 配对单量 | 423,000 | 508,000 | 465,500 | 380,500 | |
| 城市组2 | 履行单量 | 502,000 | 602,000 | 552,000 | 452,000 |
| 配对单量 | 427,000 | 512,000 | 469,500 | 384,500 | |
| 点评城市分群作用 | |||||
| 城市组1与方针DIFF | 履行单量 | -2,000 | -2,000 | -2,000 | -2,000 |
| 配对单量 | -2,000 | -2,000 | -2,000 | -2,000 | |
| 城市组2与方针DIFF | 履行单量 | 2,000 | 2,000 | 2,000 | 2,000 |
| 配对单量 | 2,000 | 2,000 | 2,000 | 2,000 | |
| 整体损失(MSE) | 64,000,000 | ||||
保存该最优试验方针分流计划及同质性点评结果,供后续环节运用
STEP 4 试验设计点评
在测验日期上,输出满意同质性规范的试验方针分流计划中,两两分组之间的中心方针相对差异,并判别差异是否明显(输出p值)
展示多个试验方针分流计划,供用户挑选
3. 事例阐明
1. 试验前差异有延续性
能够检验试验前差异和试验中差异存在相关性,若相关则阐明试验前的差异或许延续到试验中
问题:将试验前的差异操控在0邻近,是否能将试验中的差异更好地操控在0邻近?
2. 发现最优分组增强试验可靠性
简略随机分流:user_id随机分流
操控试验前差异:在user_id随机分流的基础上,只挑选两组人均单量的相对差异在0.25%以内的分流(这部分分流占整体分流大约16%)
两种抽样方法经过随机模仿各得到1000种分流,分别计算两种分流方法试验中a、b两组人均单量的相对差异
相对差异 = 试验组方针/对照组方针 – 1
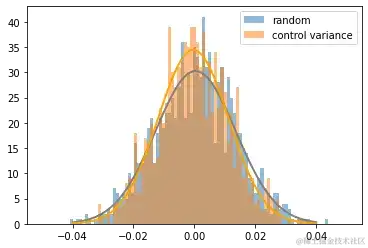
因为两组遭到的干涉相同(AA试验),故期望差异在0邻近越会集越好;越会集,阐明两组越同质,分流同质性越好
操控试验前差异能够必定程度试验中差异在0邻近的会集度,从而进步分流的同质性
左图:横轴表明试验前人均单量差异,纵轴表明试验中人均单量差异
右图:横轴表明试验中两组相对差异;纵轴表明相对差异出现的频次(大部分差异在0邻近);蓝:简略随机抽样,黄:操控试验前差异
总结
试验前误差会造成试验组和对照组之间存在差异,影响AB试验的实践作用。
本文在微软提出的SeedFinder基础上,结合运筹优化技能,提出了一种离线分流算法,在货拉拉的实践事务中取得了较好的试验作用。