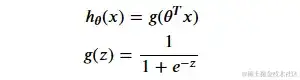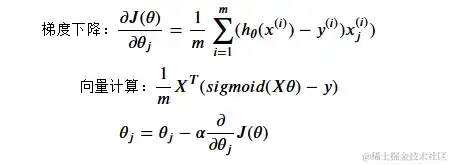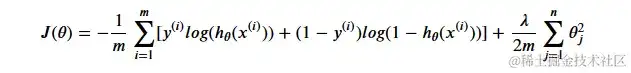温馨提示:在阅览并了解前文1.线性回归的基础上再看本文会更容易了解

1.界说，意图以及效果

界说:

逻辑回归算法是一种用于处理分类问题的机器学习算法，尽管名字中包含”回归”一词，但实践上逻辑回归是一种分类算法，而不是回归算法。逻辑回归一般用于处理二分类问题(离散值的猜测)，行将输入数据分为两个类别。它的输出是一个介于0和1之间的概率值，表明某个样本归于某个类别的概率。

意图:

逻辑回归算法依据逻辑函数（也称为Sigmoid函数）来建模输出，将线性组合的特征与Sigmoid函数结合，从而得到一个在0到1之间的概率值。在练习进程中，逻辑回归经过最大化似然函数或最小化丢失函数（比方穿插熵丢失函数）来学习模型参数，以便能够对新的样本进行分类。

效果:

逻辑回归常用于二分类问题，例如判别邮件是垃圾邮件还对错垃圾邮件、患者是否患有某种疾病等。尽管逻辑回归是一种简略的算法，但在许多实践运用中仍然十分有用，并且能够作为其他更复杂分类算法的基准。

2.算法结构

逻辑回归算法的结构相对简略而直观。让我用文字描绘一下逻辑回归算法的基本结构：

输入层：输入层接纳特征数据，每个特征对应输入层的一个节点。
权重：每个输入特征都有一个对应的权重，用来衡量该特征对终究输出的影响程度。(解说一下。这儿所谓的权重其实便是参数，有多少个特征就有多少个参数，全部的组合起来构成一个矩阵)
线性组合：输入特征和对应的权重进行线性组合，得到加权和(这儿运用矩阵进行求和核算)。
激活函数：线性组合的成果经过激活函数，一般是Sigmoid函数（也称为逻辑函数），将成果映射到[0, 1]之间，表明样本归于正类的概率。
输出层：输出层输出分类成果，一般以0.5为阈值进行分类，大于0.5为正类，小于0.5为负类。
丢失函数：经过比较模型输出和实在标签，核算丢失值，常用的丢失函数是穿插熵丢失函数。
优化算法：经过优化算法（如梯度下降）来调整模型参数，使丢失函数最小化，从而使模型能够更好地猜测样本的类别(这儿的丢失函数其实便是价值函数，经过不断梯度下降找到价值函数的最小值咱们就能够较为精确的猜测事物分类的概率，打个比方，经过梯度下降不断优化差错值后，咱们就能够经过这个模型更好地猜测该用户是否会买某件商品的或许，其间终究的输出成果只需0和1，也便是买与不买)。

总的来说，逻辑回归算法的结构包含输入层、权重、线性组合、激活函数、输出层、丢失函数和优化算法。这些组件共同效果，使得逻辑回归能够有用地进行二分类任务的猜测。期望这个扼要的描绘能协助您更好地了解逻辑回归算法的结构！

3.算法组成One-数据预备

1.读取文件，存储数据

path = 'ex2data1.txt'
# 文件路径
data = pd.read_csv(path, header=None, names=['Exam1', 'Exam2', 'Admitted'])
# 存储文件数据
data.head()
# 简化文件数据

2.提取与观测数据(注:这儿不是重点，只是经过图像的方式能让你有更直观的了解)

positive = data[data['Admitted'].isin([1])]
negative = data[data['Admitted'].isin([0])]
fig, ax = plt.subplots(figsize=(12, 8))
ax.scatter(positive['Exam1'], positive['Exam2'], s=50, c='b', marker='o', label='Admitted')
ax.scatter(negative['Exam1'], negative['Exam2'], s=50, c='r', marker='x', label='Not Admitted')
ax.legend()
ax.set_xlabel('Exam1 Score')
ax.set_ylabel('Exam2 Score')
plt.show()

这段代码是用来创立一个散点图来可视化数据会集的两个特征（Exam1 和 Exam2）和它们与是否被选取的联系。让我逐句解说一下这段代码：

positive = data[data['Admitted'].isin([1])]：这一行代码从数据会集挑选一切被选取（Admitted 为1）的数据点，并将它们存储在 positive 变量中。
negative = data[data['Admitted'].isin([0])]：这一行代码从数据会集挑选一切未被选取（Admitted 为0）的数据点，并将它们存储在 negative 变量中。
fig, ax = plt.subplots(figsize=(12, 8))：这一行代码创立了一个新的图形（figure）和一个包含单个轴（axes）的 subplot，并设置了图形的巨细为 12×8。
ax.scatter(positive['Exam1'], positive['Exam2'], s=50, c='b', marker='o', label='Admitted')：这一行代码制作了被选取的数据点，运用蓝色圆圈（marker=’o’）表明，点的巨细为 50，横坐标为 Exam1 的值，纵坐标为 Exam2 的值，标签为 ‘Admitted’。
ax.scatter(negative['Exam1'], negative['Exam2'], s=50, c='r', marker='x', label='Not Admitted')：这一行代码制作了未被选取的数据点，运用红色叉号（marker=’x’）表明，点的巨细为 50，横坐标为 Exam1 的值，纵坐标为 Exam2 的值，标签为 ‘Not Admitted’。
ax.legend()：这一行代码增加了图例，显现 ‘Admitted’ 和 ‘Not Admitted’ 对应的标签。
ax.set_xlabel('Exam1 Score')：这一行代码设置 x 轴的标签为 ‘Exam1 Score’。
ax.set_ylabel('Exam2 Score')：这一行代码设置 y 轴的标签为 ‘Exam2 Score’。
plt.show()：终究一行代码显现了制作好的散点图。

Tips:

(1).data['Admitted'].isin([1])

data['Admitted'].isin([1])这段代码是 Pandas 中的一种用法，它的效果是查看 DataFrame（数据框）中 ‘Admitted’ 列中的每个元素是否等于 1。具体来说，isin([1])办法会回来一个布尔值的 Series，其间每个元素都表明对应方位的元素是否等于 1。假如某个元素等于 1，则对应方位的值为 True，不然为 False。

在这种状况下，这段代码被用来筛选出 ‘Admitted’ 列中值为 1 的行，即被选取的数据点。这样能够方便地从数据会集提取出符合特定条件的子集，进行进一步的剖析或可视化操作。

(2).ax.scatter()

当咱们解析这段代码ax.scatter(positive['Exam1'], positive['Exam2'], s=50, c='b', marker='o', label='Admitted')时，咱们能够逐个参数来了解它的效果：

positive['Exam1']：这表明在被选取的数据会集，咱们要运用 ‘Exam1’ 列的值作为散点图中的 x 值，即被选取学生的第一次考试成绩。
positive['Exam2']：这表明在被选取的数据会集，咱们要运用 ‘Exam2’ 列的值作为散点图中的 y 值，即被选取学生的第二次考试成绩。
s=50：这个参数设置了散点的巨细为 50，表明被选取的数据点在图中的巨细。
c='b'：这个参数设置了散点的色彩为蓝色（’b’ 代表 blue），表明被选取的数据点在图中的色彩。
marker='o'：这个参数设置了散点的形状为圆圈（’o’），表明被选取的数据点在图中的形状。
label='Admitted'：这个参数设置了图例中对应这些散点的标签为 ‘Admitted’，用来区别不同类别的数据点。

综合起来，这段代码的效果是在散点图中制作被选取的学生数据点，横坐标为第一次考试成绩，纵坐标为第二次考试成绩，点的巨细为 50，色彩为蓝色，形状为圆圈，并且在图例中标记为 ‘Admitted’。这样能够直观地展现被选取学生的散布状况。

(3).fig, ax = plt.subplots(figsize=(12, 8))

这段代码fig, ax = plt.subplots(figsize=(12, 8))首要是用来创立一个新的图形（figure）和一个或多个子图（axes）方针。让我来解说一下其间的细节：

plt.subplots()是 Matplotlib 库中用于创立图形和子图的函数。在这儿，fig, ax = plt.subplots(figsize=(12, 8))创立了一个新的图形和一个子图方针。
fig是代表整个图形的方针，能够包含一个或多个子图。经过fig方针，咱们能够对整个图形进行操作，比方设置标题、保存图形等。
ax是代表子图（axes）的方针，它是实践用来制作图形元素的部分。经过ax方针，咱们能够在子图中增加各种可视化元素，比方线条、散点、文本等。
figsize=(12, 8)这个参数指定了图形的巨细，其间(12, 8)表明图形的宽度为 12 英寸，高度为 8 英寸。经过设置figsize，咱们能够控制生成的图形的尺寸，以便更好地展现数据或调整布局。

综合起来，这段代码的效果是创立一个新的图形和子图方针，图形的巨细为宽度 12 英寸，高度 8 英寸。这样能够为后续的数据可视化操作供给一个基础框架。

3.数据预备与处理

# add ones column，增加一组全1向量
data.insert(0, 'Ones', 1)
# set X(training data) and Y(target variable)
X = data.iloc[:, 0: -1].values
Y = data.iloc[:, -1].values
theta = np.zeros(3)
# 参数矩阵初始化
cost(theta, X, Y)
# 核算初始的价值，这儿的cost函数暂且看不懂没联系，下面有解说
gradient(theta, X, Y)
# 进行梯度下降求最适宜的参数矩阵，这儿的gradient函数暂且看不懂也没联系，下面有解说
# 以上大概便是简略逻辑回归的全部步骤，接下来便是独自对这几个函数进行解说

这段代码是用Python编写的，首要是用于设置练习数据和方针变量。让我逐句解说：

X = data.iloc[:, 0:-1].values: 这行代码是从数据中挑选一切行以及除终究一列之外的一切列，然后将其转换为一个NumPy数组。这儿假定data是一个DataFrame，.iloc用于经过行和列的方位挑选数据(除终究一列之外的一切列)。
Y = data.iloc[:, -1].values: 这行代码是从数据中挑选一切行以及终究一列，然后将其转换为一个NumPy数组。这儿将终究一列视为方针变量(终究一列，在分类问题中一般是由0或1构成)。
theta = np.zeros(3): 这行代码创立了一个由三个零组成的NumPy数组，用于存储模型的参数。在这儿，假定这个数组将用作线性回归模型的参数向量，其间包含截距项和特征的系数。

这些代码片段一起构成了预备线性回归模型所需的数据和参数的进程。

留意:

当数据全部预备好后X,Y,的值分别是:

X:(100,3)–>是一个100行3列的多维数组
Y:(100,)–>(100,)表明一个包含100个元素的一维数组，也能够称为一维向量。(一般默许状况下会被视为行向量而不是列向量)
:(3，)–>一个含有3个元素的数组，一般默许为行向量

必定要留意的是，这儿的X,Y,本质上都是数组而不是矩阵，但其运算和运用的时分与数组几乎并无差别，所以为了易于承受了解，本文我全选用矩阵的口吻，至于为什么是数组，由于在Python中，假如你运用的是NumPy库中的数组（numpy array），数组之间是能够进行乘法操作的。当你对两个NumPy数组进行乘法操作时，它们会履行元素等级的乘法，也便是对应方位的元素相乘。例如，假如有两个NumPy数组array1和array2，你能够经过array1 * array2来实现元素等级的乘法操作。这意味着它们的形状有必要相容，例如两个一维数组的长度有必要相同，或许关于多维数组，对应维度的巨细有必要一致。总的来说，在Python中，假如你运用NumPy库中的数组，你能够对数组之间进行乘法操作。这种元素等级的乘法能够在许多数据处理和科学核算的状况下十分有用。

4.算法组成Two-Sigmoid函数(等价于线性回归中的假定函数)

界说

Sigmoid函数是一种常用的激活函数，也称为逻辑函数，一般用于二分类问题中。别看它叫逻辑回归，其实和逻辑和回归问题没多大联系，逻辑是由于音译的原因，回归的话大概率是由于凭借了回归的思想原理。

在逻辑回归中，Sigmoid函数扮演着要害的角色。逻辑回归是一种广泛运用于分类问题的机器学习算法，它的方针是将输入特征映射到一个介于0和1之间的概率值，表明某个样本归于正类的概率。Sigmoid函数的效果是将逻辑回归模型的输出转换为这种概率值。

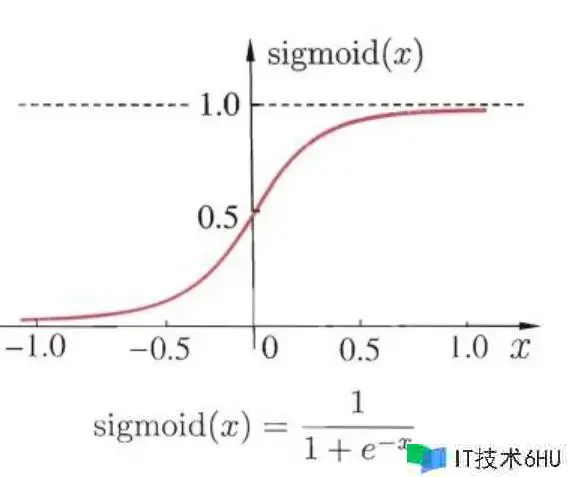
Sigmoid函数具有S形状曲线，当z趋近于正无穷大时，Sigmoid函数的值趋近于1；当z趋近于负无穷大时，Sigmoid函数的值趋近于0。这种性质使得Sigmoid函数在将实数映射到概率值时十分有用。

具体来说，逻辑回归模型会对输入特征进行加权求和，并将成果输入到Sigmoid函数中，该函数将实数值映射到0到1之间。这样，关于给定的输入特征，逻辑回归模型会输出一个介于0和1之间的概率值，表明该样本归于正类的或许性。

经过Sigmoid函数的效果，逻辑回归模型能够进行二分类猜测，将接连的实数输出转换为概率值，并依据设定的阈值来判别样本归于哪个类别。这种机制使得逻辑回归成为处理二分类问题的一种强壮东西。

代码复现

def sigmoid(z):
    return 1 / (1 + np.exp(-z))

这儿的z便是的转置乘以特征矩阵x，也便是^(T)X，在这段代码中的话没有对z进行拓宽和细节化处理，能够增加程序以及函数的灵活性

5.算法组成Three-价值函数

引入:已然咱们知道了拟合函数，知道了咱们终究的意图便是经过这个函数更好去猜测一个介于0~1的概率值，那么咱们就需求找到一组适宜的参数来最大极限地减少其间猜测值和实在值的总差错(尽管实在值不是0便是1，可是猜测值不必定总是整数的1或0)，此刻咱们就能够经过结构价值函数找出总差错值最小的那组系数。

界说以及解说:

参照前文线性回归价值函数的公式，咱们发现在逻辑回归中多了取对数的操作，也便是log()，为什么呢?这儿我只能大略的解说，总归终究的意图是为了能够使咱们终究得出来的猜测值更加精确精确，假如你想搞懂的话，引荐一篇讲的还不错的文章用人话讲了解逻辑回归Logistic regression

其次，咱们发现该价值函数分红了两段，这又是为什么?

逻辑回归中的价值函数一般是由两部分组成的，这种规划有其特定的含义和效果。在逻辑回归中，常用的价值函数是穿插熵丢失函数（Cross-Entropy Loss）。这个丢失函数在逻辑回归中被广泛运用，由于它能很好地衡量模型输出与实践标签之间的差异。

穿插熵丢失函数的两段分别是针对正类别和负类别的状况。

这种两段式的规划使得价值函数能够更好地对模型的猜测进行赏罚，当模型的猜测与实践标签不一致时，会发生较大的丢失。经过这种规划，模型在练习进程中能够更好地学习正确的分类鸿沟，进步分类的精确性。

总的来说，逻辑回归中价值函数分红两段的规划有助于模型更好地学习和调整参数，使得模型能够更精确地猜测样本的分类状况。这种价值函数的规划有助于进步模型的性能和泛化才干(提示一下，有些知识点或许定论不要求必定要搞懂，由于必定要搞懂的话就需求伴随着数学的推理进程，了解与清楚有些时分或许更为重要)。

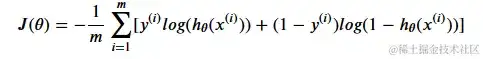
代码复现

def cost(theta, X, Y):
    first = Y * np.log(sigmoid(X@theta.T))
    second = (1 - Y) * np.log(1 - sigmoid(X@theta.T))
    return -1 * np.mean(first + second)

经过这个函数，咱们就能求出关于某组参数值所对应的价值值，然后经过比较每组值的价值值巨细来选出最适宜，差错最小，拟合效果最好的参数矩阵。那么问题来了，咱们怎么更新参数矩阵呢?便是梯度下降了。

算法组成Four-梯度下降

代码复现:

办法一

# 核算步长
def gradient(theta, X, Y):
    return (1/len(X) * X.T @ (sigmoid(X @ theta.T) - Y))
# 运用Scipy.optimize.fmin_tnc优化函数拟合最优的
import scipy.optimize as opt
result = opt.fmin_tnc(func=cost, x0=theta, fprime=gradient, args=(X, Y))
result     #(array([-25.16131862, 0.20623159, 0.20147149]), 36, 0)
# 这儿是为了输出，更直观的看看
cost(result[0], X, Y)

scipy.optimize.fmin_tnc是SciPy库中的一个函数，用于履行无束缚最小化（优化）问题的优化算法。TNC 代表 Truncated Newton Conjugate-Gradient，是一种依据牛顿共轭梯度办法的优化算法。这个函数的首要效果是寻觅使得给定方针函数最小化的参数值。在优化进程中，它运用梯度信息来迭代地调整参数值，以便找到使方针函数最小化的最优解。

scipy.optimize.fmin_tnc函数一般需求供给以下几个参数：

方针函数（一般是一个 Python 函数）
初始参数值
梯度函数（可选）
其他优化参数，如容差值、最大迭代次数等

经过调用scipy.optimize.fmin_tnc函数，能够方便地在 Python 中进行数值优化，寻觅方针函数的最小值。这个函数在处理大规模的无束缚优化问题时十分有用，尤其是当方针函数具有复杂的方式或许无法经过解析办法求解时。

办法二:

# 传统梯度下降法
theta = np.matrix(theta)
X = np.matrix(X)
Y = np.matrix(Y)
parameters = int(theta.ravel().shape[1])
grad = np.zeros(parameters)
print(X.shape, theta.shape, (theta.T).shape, (X*theta.T).shape)
error = sigmoid(X * theta.T) - Y
for i in range(parameters):
   term = np.multiply(error, X[:, i])
   grad[i] = np.sum(term) / len(X)
return grad

让我逐句来解说一下：

theta = np.matrix(theta): 将参数theta转换为 NumPy 矩阵。
X = np.matrix(X): 将特征矩阵X转换为 NumPy 矩阵。
Y = np.matrix(Y): 将标签矩阵Y转换为 NumPy 矩阵。
parameters = int(theta.ravel().shape[1]): 核算参数的数量。
grad = np.zeros(parameters): 创立一个全零数组，用于存储梯度。
print(X.shape, theta.shape, (theta.T).shape, (X*theta.T).shape): 打印出各个矩阵的形状，用于调试和验证维度匹配。
error = sigmoid(X * theta.T) - Y: 核算猜测值与实践值之间的差错。
for i in range(parameters):: 开端一个循环，遍历每个参数。
term = np.multiply(error, X[:, i]): 核算差错与特征矩阵的乘积。
grad[i] = np.sum(term) / len(X): 核算梯度的第i个元素。
return grad: 回来核算得到的梯度数组。

这段代码的意图是核算逻辑回归模型的梯度，用于更新参数以最小化丢失函数。

办法三:

# 运用Scipy.optimize.minimize拟合最优的theta
res = opt.minimize(fun=cost, x0=np.array(theta), args=(X, np.array(Y)), method='Newton-CG', jac=gradient)
res
#成果: fun: 0.20349770451259855 
#    jac: array([1.62947970e-05, 1.11339134e-03, 1.07609314e-03]) 
#    message: 'Optimization terminated successfully.' 
#    nfev: 71 
#    nhev: 0 
#    nit: 28 
#    njev: 242 
#    status: 0 
#    success: True 
#    x: array([-25.16576744, 0.20626712, 0.20150754])   (这儿便是咱们想要的theta矩阵)
cost(res.x, X, Y)

scipy.optimize.minimize是 SciPy 库中一个十分强壮的函数，用于处理多种数学优化问题，包含最小化或最大化标量函数、束缚优化、大局优化等。这个函数供给了一个统一的接口，能够经过指定不同的办法和选项来处理各种优化问题。

运用scipy.optimize.minimize能够经过指定方针函数、初始猜测值、优化办法、束缚条件等参数来寻觅方针函数的最小值或最大值。它支持多种优化算法，如共轭梯度法、BFGS 算法、L-BFGS-B 算法等，以及处理束缚优化问题的办法。

一般来说，scipy.optimize.minimize函数需求供给以下几个参数：

方针函数
初始参数值
优化办法（如 BFGS、Nelder-Mead、COBYLA 等）
束缚条件（可选）
其他优化参数，如容差值、最大迭代次数等

经过调用scipy.optimize.minimize函数，能够在 Python 中方便地进行各种数学优化问题的求解，无论是简略的无束缚优化问题还是复杂的带束缚优化问题。这个函数在科学核算、机器学习、工程优化等范畴都有广泛的运用。

办法一和办法三是凭借优化函数库，办法二是传统的梯度下降

好了，到这儿咱们应该就能得到一个拟合效果相对较好的假定函数了，接下来便是运用该函数进行猜测剖析并且核算校验一下该模型的精确率

算法组成Five-猜测剖析

由于逻辑回归不同于线性回归对接连值的猜测，所核算出来的值便是成果值，逻辑回归首要还是分类问题，需求将核算所得的成果进行恰当处理以求得到终究的成果

模型运用与猜测:

def predict(theta, X):
    probability = sigmoid(X @ theta.T)
    return [1 if x >= 0.5 else 0 for x in probability]

X为特征矩阵，theta为之前求出来的较适宜的参数组，这儿的输出值也便是每一个样本的分类成果(对应0或1两种)

算法组成Six-模型精确率

那么咱们已然运用模型猜测出了对应成果，不妨看看咱们的模型的猜测成果的精确率是多少(这儿说一下，之前的猜测不是真的”猜测”，需求咱们同时也拿到Y值实在成果，只需这样子才干判别咱们练习出来的模型准不精确)

模型精确率核算:

theta_min = np.matrix(result[0])
predictions = predict(theta_min, X)
correct = [1 if a^b == 0 else 0 for (a,b) in zip(predictions, Y)]
accuracy = (sum(correct) / len(correct))
print('accuracy = {0:.0f}%'.format(accuracy*100))

当你履行这段代码时，它做了以下几件事情：

theta_min = np.matrix(result[0])：这行代码将优化成果result中的第一个元素（一般是优化得到的参数向量）转换为 NumPy 矩阵，并赋值给theta_min。这个参数向量一般代表着优化后的最优参数值(这儿的result[0]对应的上面梯度下降的第一个办法所求出来的result)。
predictions = predict(theta_min, X)：这行代码调用一个名为predict的函数，传入theta_min和输入数据X，然后生成猜测值predictions。这个步骤用最优参数对输入数据进行猜测。
correct = [1 if a^b == 0 else 0 for (a,b) in zip(predictions, Y)]：这行代码经过遍历predictions和实践标签Y，创立一个列表correct。在这个列表中，假如猜测值和实践标签相同，则对应方位为1，不然为0。这样能够判别每个样本的猜测是否正确。
accuracy = (sum(correct) / len(correct))：这行代码核算了正确猜测的样本数量，并除以总样本数量，得到精确率accuracy。这是经过将correct列表中的1的总和除以总样本数来核算的。
print('accuracy = {0:.0f}%'.format(accuracy*100))：终究一行代码将精确率以百分比的方式打印出来。经过格式化字符串，将精确率乘以100后保存整数部分，并输出到控制台，显现终究的精确率成果。

这段代码首要用于评估一个模型的精确率，经过比较模型猜测成果和实践标签，然后核算出精确率并输出。

tips:

(1)

zip(predictions, Y)是 Python 中的一个内置函数，它承受多个可迭代方针作为参数，并回来一个将这些可迭代方针中对应方位的元素打包成元组的迭代器。

在这种状况下，zip(predictions, Y)将两个可迭代方针predictions和Y中对应方位的元素一一配对，构成一个迭代器。例如，假如predictions是[0, 1, 0]，Y是[1, 1, 0]，那么zip(predictions, Y)将生成一个迭代器，其间第一个元素是(0, 1)，第二个元素是(1, 1)，第三个元素是(0, 0)。

在上面提到的代码中，zip(predictions, Y)的效果是将模型的猜测值predictions和实践标签Y对应方位的元素配对，这样能够方便地同时遍历这两个列表，进行比较和操作。

(2)

这行代码中的1 if a^b == 0 else 0是一个条件表达式，也称为三元运算符。它的效果是依据条件a^b == 0的真假来回来不同的值。在这儿，a^b表明 a 和 b 的异或运算，即按位异或操作。(在许多编程语言中，包含Python，符号一般用来表明按位异或运算，而不是乘方运算。在Python中，运算符被用于履行位运算，对两个数的二进制位进行异或操作。假如你想进行乘方运算，应该运用**运算符，而不是。所以在这种状况下，a^b表明的是 a 和 b 的按位异或运算，而不是乘方运算。假如 a 和 b 持平，那么 a 和 b 的每一位都是相同的，因而它们的异或操作成果为 0。换句话说，假如 a 和 b 持平，那么 a^b 的值将为 0。而假如 a 和 b 不持平，那么它们的二进制表明中至少有一位是不同的。在这种状况下，进行异或操作会使得对应的位为 1。所以，假如 a 和 b 不持平，a^b 的值将不为 0。)

假如a^b的成果等于 0，那么条件a^b == 0就为真，此刻该条件表达式会回来 1；不然，即a^b != 0，条件表达式回来 0。

因而，整个列表推导式correct = [1 if a^b == 0 else 0 for (a,b) in zip(predictions, Y)]的效果是依据predictions和Y中对应方位的元素进行异或运算，假如成果为 0，则对应方位的correct列表中的元素为 1，不然为 0。这样能够依据模型的猜测值和实践标签的异或成果来判别猜测是否正确，并将成果存储在correct列表中。

拓宽

1.那么以上便是基础的模型框架了，假如你想对该模型了解的更深一点，那么还有查准率，召回率，调和平均数这几个数值能够调

# support标签中出现的次数
# precision查准率，recall召回率，f1-score调和平均数
from sklearn.metrics import classification_report
print(classification_report(Y, predictions))

关于这儿的这三个率是什么意思我后面会讲。

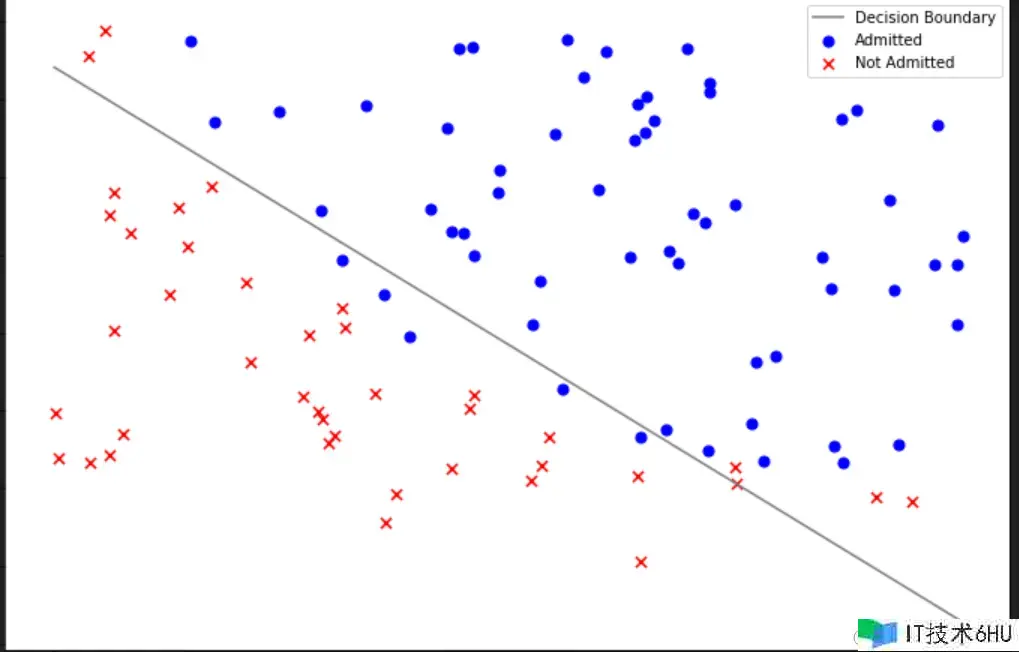
2.决策鸿沟:

coef = -res.x / res.x[2]
x = np.arange(30, 100, 0.5)
y = coef[0] + coef[1] * x
fig, ax = plt.subplots(figsize=(12, 8))
ax.scatter(positive['Exam1'], positive['Exam2'], s=50, c='b', marker='o', label='Admitted')
ax.scatter(negative['Exam1'], negative['Exam2'], s=50, c='r', marker='x', label='Not Admitted')
ax.plot(x, y, label='Decision Boundary', c='grey')
ax.legend()
ax.set_xlabel('Exam1 Score')
ax.set_ylabel('Exam2 Score')
plt.show()

咱们便是依据该样本点落在这条拟合线的左右两头来判别出终究成果的

3.特征映射

def feature_mapping(x, y, power, as_ndarray=False):
    data = {'f{0}{1}'.format(i-p, p): np.power(x, i-p) * np.power(y, p)
                for i in range(0, power+1)
                for p in range(0, i+1)
           }
    if as_ndarray:
        return pd.DataFrame(data).values
    else:
        return pd.DataFrame(data)

这段代码是一个Python函数，名为feature_mapping，用于进行特征映射。让我逐句解说它：

def feature_mapping(x, y, power, as_ndarray=False):
- 这是界说函数的行，函数名为feature_mapping，承受四个参数：x，y，power，以及一个可选的参数as_ndarray，用于指示是否将成果转换为NumPy数组。
data = {'f{0}{1}'.format(i-p, p): np.power(x, i-p) * np.power(y, p) for i in range(0, power+1) for p in range(0, i+1) }
- 这一行是一个字典推导式，用于生成特征映射后的数据。它会生成一个字典，其间键为’f{0}{1}’.format(i-p, p)，值为x的(i-p)次方乘以y的p次方，i和p的取值范围由range函数确定。
if as_ndarray:
- 这行代码查看是否需求将成果转换为NumPy数组。
return pd.DataFrame(data).values
- 假如as_ndarray为True，函数将回来data字典转换为DataFrame后的值数组。
else:
- 假如as_ndarray为False，即默许状况下，函数将回来data字典转换为DataFrame后的DataFrame方针。

这段代码首要完成了一个特征映射的进程，能够将输入的x和y映射到更高维度的特征空间中。期望这个解说能够协助你了解这段代码的功能。假如有任何其他问题或需求更多解说，请随时告诉我。

当考虑一个简略的特征映射示例时，咱们能够想象一个二维数据集，其间包含一些数据点，它们无法经过一条直线进行良好的分类。这时，咱们能够运用特征映射将这些数据点映射到一个更高维的空间，以便更好地进行分类。

假定咱们有一个二维数据集，包含两个特征：x1和x2。在二维空间中，这些数据点或许无法经过一条直线很好地分隔两个类别。可是，假如咱们将这些二维数据点经过特征映射映射到三维空间，咱们能够增加一个新的特征
x3=x12+x22
. 这样，咱们就将二维数据映射到了一个更高维的三维空间。

在这个新的三维空间中，数据点或许会呈现出线性可分的特性，即存在一个平面能够很好地将两个类别分隔。经过这种方式，咱们运用特征映射将原始数据转换为一个更适合分类的方式。

这个简略的例子展现了特征映射怎么能够协助咱们处理原始数据，并使得数据更容易分类。

简略例子:

想象一下你正在预备烤蛋糕。在配方中，你有两种质料：面粉和砂糖。现在，你想要依据这两种质料的不同份额来判别蛋糕的口感是甜蜜还是偏向面粉味。

在原始的二维空间中，你只能看到面粉和砂糖的份额，无法精确判别口感。可是，经过特征映射，你能够引入一个新的特征，比方面粉的平方加上砂糖的平方，这样就将二维空间映射到了三维空间。

在这个新的三维空间中，你能够更好地区别不同口感的蛋糕。比方，假如面粉和砂糖的平方和较大，或许代表口感更甜蜜；反之，假如平方和较小，或许代表口感更偏向面粉味。

经过这种特征映射，你在更高维度的空间中能够更好地了解和分类不同口感的蛋糕，就像在二维空间中无法做到的那样。

好了，现在咱们对大致模型已经有了基本的概念，但咱们有没有考虑过这样一个问题，当咱们经过过多次数的迭代，使得到的参数矩阵越来越精确，拟合效果越来越好，输出值越来越挨近实在值，那么当终究拟合的数据与实在值彻底持平的时分，拟合的数据确实是100%精确了，可是这样不但会形成拟合的函数歪曲，形状怪异，还会大大减少拟合函数的猜测效果和泛化才干，这便是所谓的过拟合问题了。同样的，欠拟合问题也是如此，都是由于一个适宜的迭代次数的问题，那么咱们在遇到如此问题的时分该怎么处理呢?那便是，正则化!

算法惩戒准则-正则化

1.价值函数正则化

在这儿咱们对价值函数加上正则化代码复现:

# 特征映射与数据预备
theta = np.zeros(data.shape[1])
X = feature_mapping(x1, x2, power=6, as_ndarray=True)
X.shape, Y.shape, theta.shape
# Sigmoid激活函数
def sigmoid(z):
    return 1 / (1 + np.exp(-z))
# 基础价值函数
def cost(theta, X, Y):
    first = Y * np.log(sigmoid(X@theta.T))
    second = (1 - Y) * np.log(1 - sigmoid(X@theta.T))
    return -1 * np.mean(first + second)
# 正则化价值函数
def regularized_cost(theta, X, Y, l=1):
    theta_1n = theta[1:]
    regularized_term = l / (2 * len(X)) * np.power(theta_1n, 2).sum()
    return cost(theta, X, Y) + regularized_term
# 运行正则化价值函数
cost(theta, X, Y)
regularized_cost(theta, X, Y, l=1)

regularized_term = l / (2 * len(X)) * np.power(theta_1n, 2).sum()代码解说(其他部分请看前面):

regularized_term: 这是要核算的正则化项的成果，即正则化项的值。
l: 这是正则化参数（lambda），用于控制正则化的强度。
len(X): 这儿是X的长度，表明练习样本的数量。
np.power(theta_1n, 2): 这部分核算了参数向量theta的每一个元素的平方。
.sum(): 这是对上述平方值进行求和操作。

综合起来，这行代码的效果是：

首先，核算了参数向量theta的第一个元素的平方。
然后，将这个平方值求和。
接着，将这个求和值乘以正则化参数lambda除以2倍练习样本数量len(X)。

这个核算进程是正则化项的一部分，用于在练习模型时赏罚模型复杂度，避免过拟合。正则化项一般将模型参数的平方和加入到丢失函数中，以保证模型不会过度依赖于任何一个特征，从而进步模型的泛化才干

2.正则化梯度

代码复现:

# 基础梯度下降
def gradient(theta, X, Y):
    return (1/len(X) * X.T @ (sigmoid(X @ theta.T) - Y))
# 正则化梯度下降
def regularized_gradient(theta, X, Y, l=1):
    theta_1n = theta[1:]
    regularized_theta = l / len(X) * theta_1n
#     regularized_theta[0] = 0
    regularized_term = np.concatenate([np.array([0]), regularized_theta])
    return  gradient(theta, X, Y) + regularized_term
#     return  gradient(theta, X, Y) + regularized_theta
gradient(theta, X, Y)
regularized_gradient(theta, X, Y)

regularized_term = np.concatenate([np.array([0]), regularized_theta])代码解说:

这段代码中，regularized_term = np.concatenate([np.array([0]), regularized_theta])的意图是创立一个新的参数向量regularized_term，其间包含了一个额定的零值作为第一个元素，然后将regularized_theta中的一切元素顺次增加到新向量中。

让我来具体解说一下这行代码的效果：

np.array([0]): 这部分代码创立了一个包含单个零值的NumPy数组。这个零值将作为新参数向量regularized_term的第一个元素。
regularized_theta: 这是经过正则化处理后的参数向量，其间包含了要增加到新向量中的一切元素。
np.concatenate(): 这是NumPy函数，用于衔接（concatenate）数组。在这儿，它将上述两个数组衔接起来，将第一个数组[0]作为第一个元素，然后将regularized_theta中的一切元素顺次增加到新向量中。

因而，全体来说，这行代码的效果是创立一个新的参数向量regularized_term，其间包含了一个额定的零值作为第一个元素，然后将regularized_theta中的一切参数顺次增加到新向量中。这种操作一般用于在某些机器学习算法中对参数向量进行处理或扩展。

经过这两个梯度下降，只需咱们挑选较适宜的值，就能起到对欠拟合和过拟合很好的束缚效果!

以上便是第二部分关于逻辑回归算法的全部了，假如咱们有疑惑或许文章有问题，欢迎沟通

人工智能机器学习算法总结–2.逻辑回归算法

温馨提示:在阅览并了解前文1.线性回归的基础上再看本文会更容易了解

1.界说，意图以及效果

2.算法结构

3.算法组成One-数据预备

Tips:

留意:

4.算法组成Two-Sigmoid函数(等价于线性回归中的假定函数)

界说

代码复现

5.算法组成Three-价值函数

界说以及解说:

代码复现

算法组成Four-梯度下降

算法组成Five-猜测剖析

算法组成Six-模型精确率

tips:

拓宽

算法惩戒准则-正则化

1.价值函数正则化

2.正则化梯度

作者信息

人工智能机器学习算法总结–2.逻辑回归算法

温馨提示:在阅览并了解前文1.线性回归的基础上再看本文会更容易了解

1.界说，意图以及效果

2.算法结构

3.算法组成One-数据预备

Tips:

留意:

4.算法组成Two-Sigmoid函数(等价于线性回归中的假定函数)

界说

代码复现

5.算法组成Three-价值函数

界说以及解说:

代码复现

算法组成Four-梯度下降

算法组成Five-猜测剖析

算法组成Six-模型精确率

tips:

拓宽

算法惩戒准则-正则化

1.价值函数正则化

2.正则化梯度

相关文章

8 个对前端开发者有用的工具🦄

OpenAI 发布 GPT-4，有哪些技术上的优化或突破？

java中常见的对象转换工具

Flutter iOS输入法 Bug Fix 记录

作者信息