某华为hr擅自报名机考
上周,牛客网一位同学爆料:
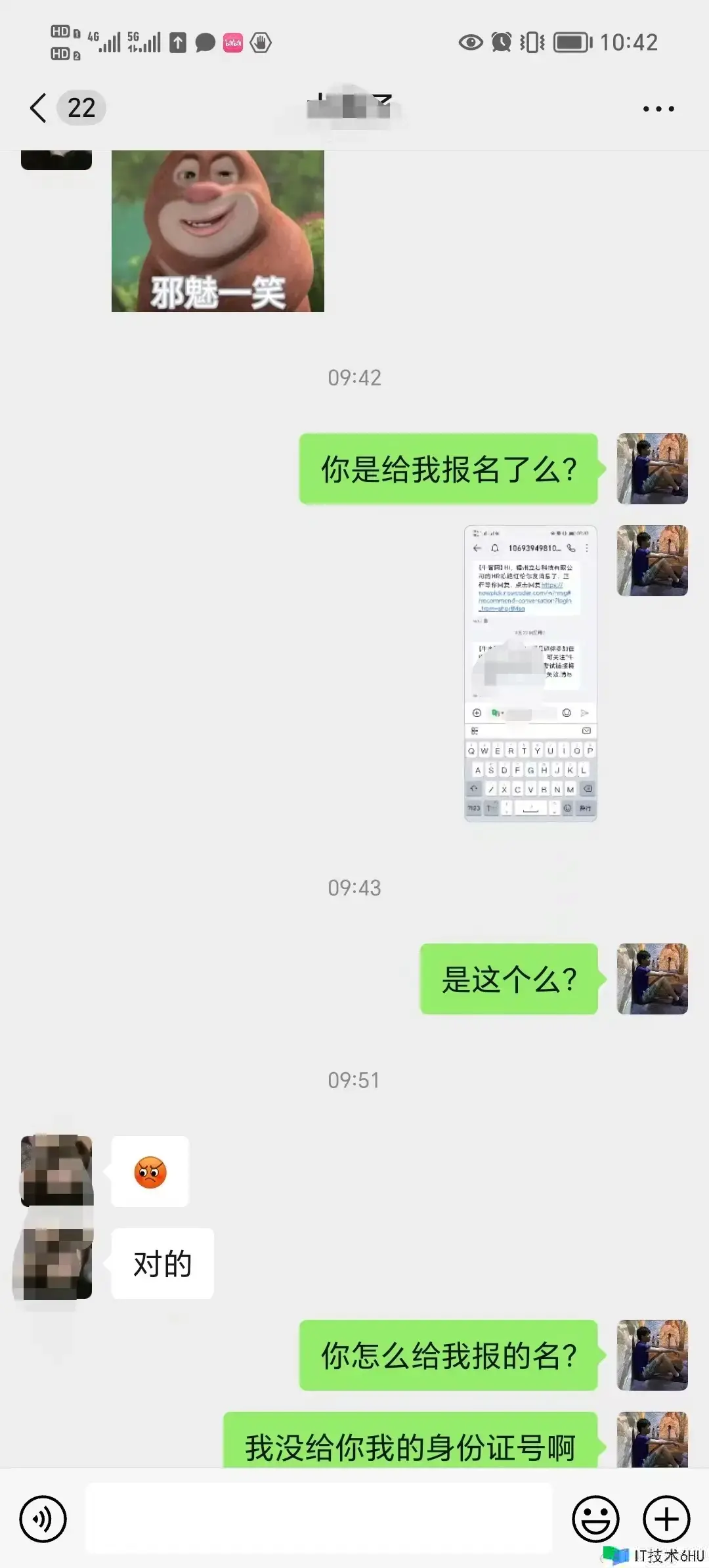
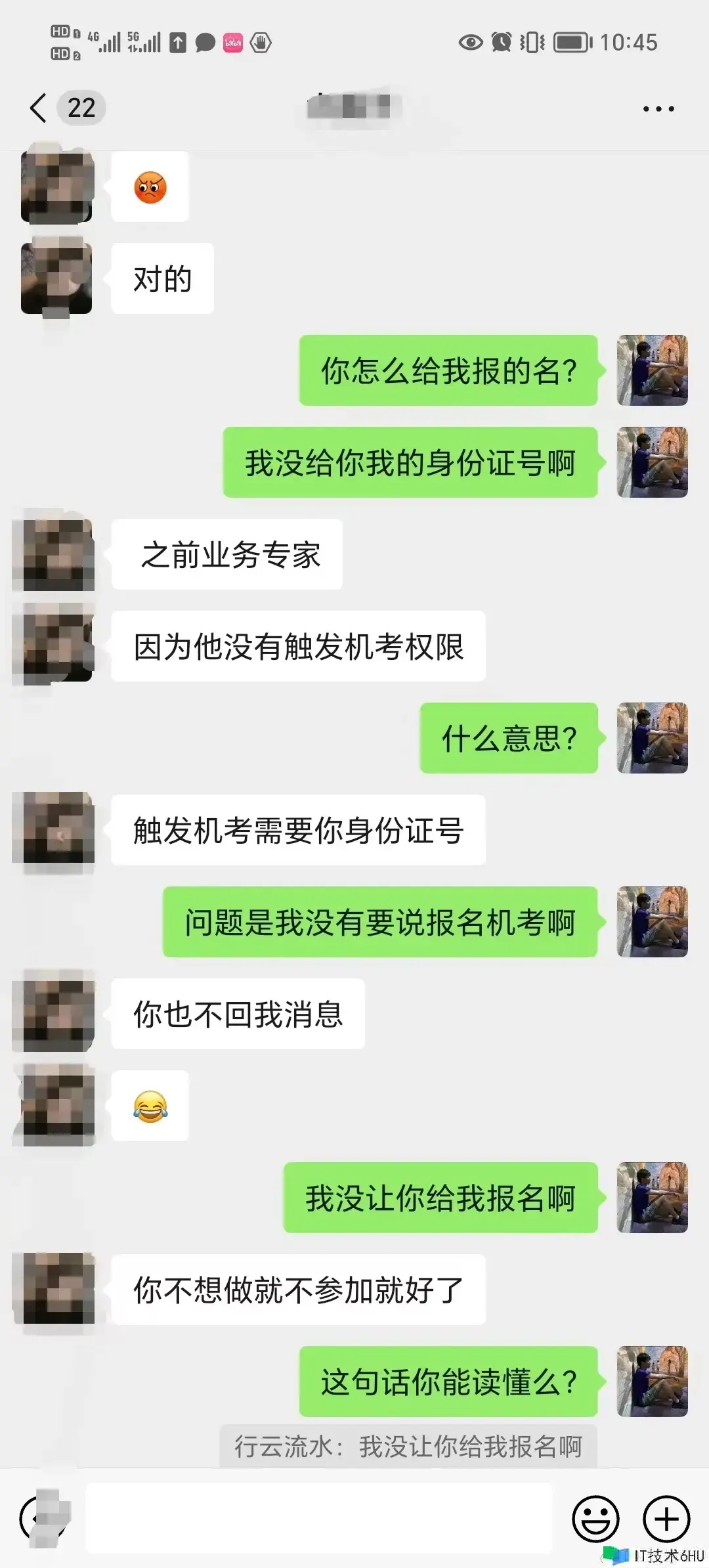
今年一月份,华为一位 HR 通过某招聘网站联系到他,然后通过该 HR 加上了业务工程师的微信。随后,该工程师在「经过他本人同意」的情况下,在系统录入了他的简历和身份证。结果,HR 在「没有和他本人沟通,也没和业务工程师沟通」的情况下,擅自在系统里触发了机考流程。
这位同学还在帖子里晒出了聊天记录截图:
在我看来,候选人生气是应该的,而且生气的原因,极有可能不是因为不想去华为,而是想去华为。
在没有与候选人沟通的情况下,HR 于情于理都不该进行这样的操作。
至少要确认给候选人定的机试时间是否合适,这是必须的。
根据帖子回复,这位同学目前正在寻求举报该 HR 的合适渠道。
关于该华为 HR 的行为,你怎么看?
…
回归主线。
来一道和「字节跳动」相关的算法原题。
题目描述
平台:LeetCode
题号:2246
给你一棵 树(即一个连通、无向、无环图),根节点是节点 0,这棵树由编号从 0 到 n - 1 的 n 个节点组成。
用下标从 0 开始、长度为 n 的数组 parent 来表示这棵树,其中 parent[i] 是节点 i 的父节点,由于节点 0 是根节点,所以 parent[0] = -1。
另给你一个字符串 s,长度也是 n,其中 s[i] 表示分配给节点 i 的字符。
请你找出路径上任意一对相邻节点都没有分配到相同字符的 最长路径 ,并返回该路径的长度。
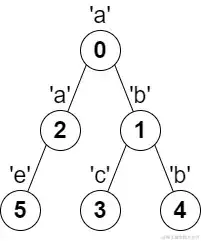
输入:parent = [-1,0,0,1,1,2], s = "abacbe"
输出:3
解释:任意一对相邻节点字符都不同的最长路径是:0 -> 1 -> 3 。该路径的长度是 3 ,所以返回 3 。
可以证明不存在满足上述条件且比 3 更长的路径。
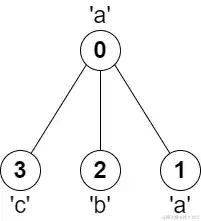
输入:parent = [-1,0,0,0], s = "aabc"
输出:3
解释:任意一对相邻节点字符都不同的最长路径是:2 -> 0 -> 3 。该路径的长度为 3 ,所以返回 3 。
提示:
- n=parent.length=s.lengthn = parent.length = s.length
- 1<=n<=1051 <= n <= 10^5
- 对所有
i >= 1,0 <= parent[i] <= n - 1均成立 - parent[0]=−1parent[0] = -1
-
parent表示一棵有效的树 -
s仅由小写英文字母组成
DFS
起始先用 parent 进行建图,随后设计 DFS 函数来求解每个节点“往下”的最长路径:将当前节点 cur 作为传入参数,返回以节点“往下”的最长路径。
这是一个由子节点最长路径推导父节点最长路径的「自下而上」的推导过程。
先来关注该
DFS的功能本身:
假设当前处理到的节点为 u,将要访问到的节点为 j。递归调用 DFS 函数拿到以节点 j 为根节点时的“往下”最大路径 t,并执行如下处理流程:
- 若节点
j和节点u对应字符相同,说明将节点j拼接在节点u后面并非合法路径,跳过处理 - 否则使用
t来更新以当前节点u为根时,最大的“往下”子路径res(该值初始值为0)
当处理完节点 u 的所有子节点,我们 res + 1 即是函数返回值(含义为在合法的最长路径本身拼接节点 u)。
再来关注
DFS过程中,如何计算问题答案:
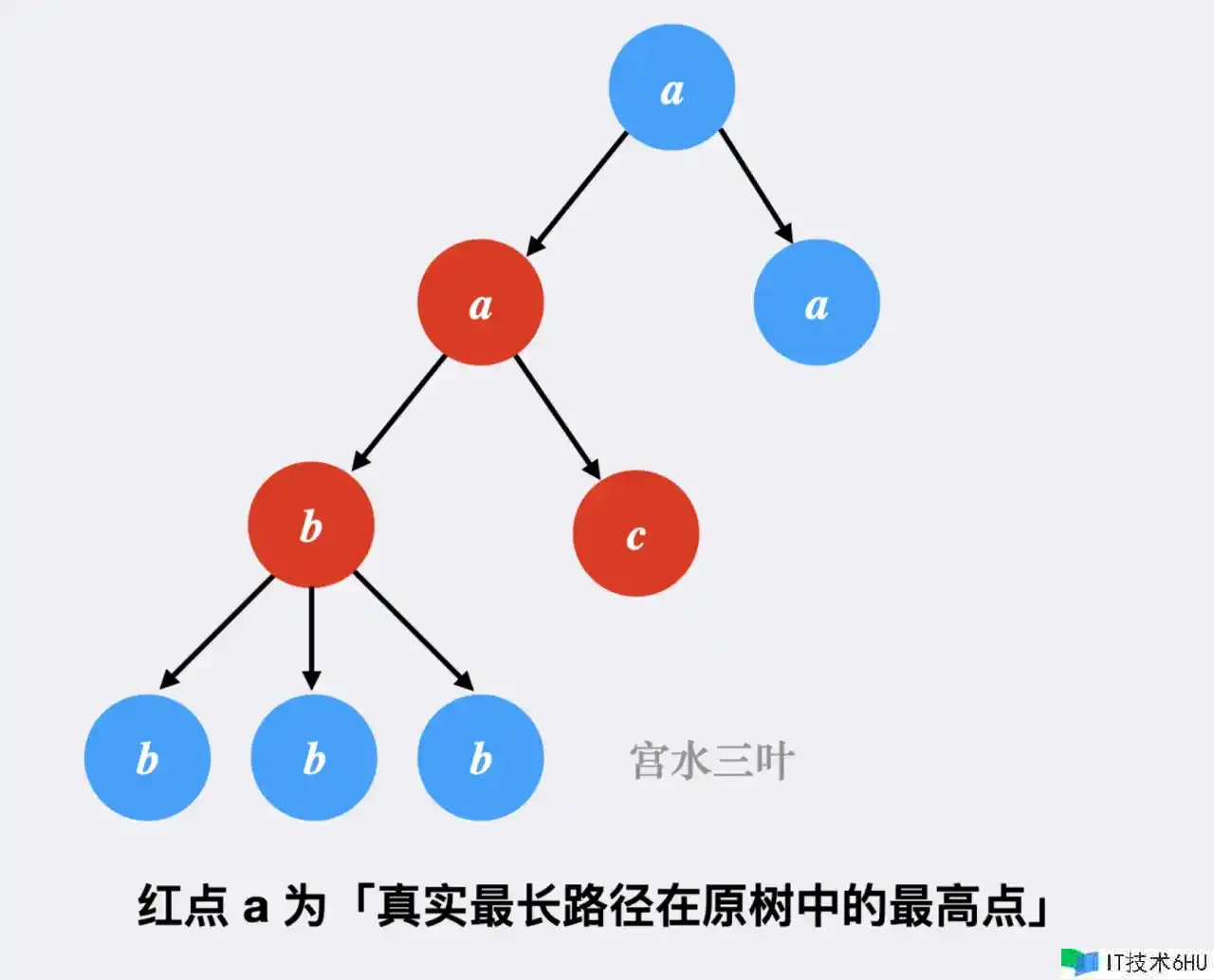
在 DFS 函数中,我们递归处理了所有节点,而在真实最长路径在原树中的最高点,自然也是被处理到的。
这引导我们可以在单次递归,处理当前节点时,使用变量 l1 和 l2 分别记录当前节点的「最大子路径」和「次大子路径」。
在处理完当前节点后,1 + l1 + l2 即是以当前节点作为路径最高点时的最大路径长度(含义为在合法「最大子路径」和「次大子路径」基础上拼接当前节点),用其更新全局变量 ans。
代码:
class Solution {
int N = 100010, M = N, idx = 0, ans = 1;
int[] he = new int[N], e = new int[M], ne = new int[M];
char[] cs;
void add(int a, int b) {
e[idx] = b;
ne[idx] = he[a];
he[a] = idx++;
}
public int longestPath(int[] parent, String s) {
Arrays.fill(he, -1);
for (int i = 1; i < parent.length; i++) add(parent[i], i);
cs = s.toCharArray();
dfs(0);
return ans;
}
int dfs(int u) {
int res = 0;
int l1 = 0, l2 = 0;
for (int i = he[u]; i != -1; i = ne[i]) {
int j = e[i];
int t = dfs(j);
if (cs[u] == cs[j]) continue;
if (t > l1) {
l2 = l1; l1 = t;
} else if (t > l2) {
l2 = t;
}
res = Math.max(res, t);
ans = Math.max(ans, 1 + l1 + l2);
}
return res + 1;
}
}
- 时间复杂度:O(n)O(n)
- 空间复杂度:O(n)O(n)
树形 DP
自然也是能够使用「树形 DP」思路来做。
只不过对于「定根树形 DP」来说,往往一遍 DFS 就能实现 O(n)O(n) 做法。例如 124. 二叉树中的最大路径和。
而「换根树形 DP」则只能通过对“方向”的拆分,用两遍 DFS 来进行求解。例如 310. 最小高度树 和 834. 树中距离之和。
在「定根树形 DP」题目中采用「换根树形 DP」做法,无论是从执行流程还是编码来说,都稍显“多余”(毕竟一次 DFS 就能以「最佳路径的最高点必然能够被处理」来得证答案的正确性),但在验证大家是否真正掌握「树形 DP」精髓来说,却有极大意义。
代码:
class Solution {
int N = 100010, M = N, idx = 0;
int[] he = new int[N], e = new int[M], ne = new int[M];
char[] cs;
int[] f1 = new int[N], f2 = new int[N], g = new int[N], p = new int[N];
void add(int a, int b) {
e[idx] = b;
ne[idx] = he[a];
he[a] = idx++;
}
public int longestPath(int[] parent, String s) {
Arrays.fill(he, -1);
for (int i = 1; i < parent.length; i++) add(parent[i], i);
cs = s.toCharArray();
dfs1(0);
dfs2(0);
int ans = 1;
int[] temp = new int[3];
for (int i = 0; i < parent.length; i++) {
temp[0] = f1[i]; temp[1] = f2[i]; temp[2] = g[i];
Arrays.sort(temp);
ans = Math.max(ans, 1 + temp[1] + temp[2]);
}
return ans;
}
int dfs1(int u) {
int ans = 0;
for (int i = he[u]; i != -1; i = ne[i]) {
int j = e[i];
int t = dfs1(j);
if (cs[u] == cs[j]) continue;
if (t > f1[u]) {
f2[u] = f1[u]; f1[u] = t;
p[u] = j;
} else if (t > f2[u]) {
f2[u] = t;
}
ans = Math.max(ans, t);
}
return ans + 1;
}
void dfs2(int u) {
for (int i = he[u]; i != -1; i = ne[i]) {
int j = e[i];
if (cs[u] != cs[j]) {
// 往上再往上
g[j] = g[u] + 1;
// 往上再往下(根据 u 的往下最大路径是否由 j 参与决定使用 最大值 还是 次大值)
if (p[u] != j) g[j] = Math.max(g[j], 1 + f1[u]);
else g[j] = Math.max(g[j], 1 + f2[u]);
}
dfs2(j);
}
}
}
- 时间复杂度:常数较大的 O(n)O(n)。相比于一次
DFS的做法来说,额外多了一次DFS,以及构建答案时对定长数组的排序操作 - 空间复杂度:O(n)O(n)
最后
给大伙通知一下 :
全网最低价 LeetCode 会员目前仍可用!!!
年度会员:有效期加赠两个月!!; 季度会员:有效期加赠两周!!
年度会员:获 66.66 现金红包!!; 季度会员:获 22.22 现金红包!!
年度会员:参与当月丰厚专属实物抽奖(中奖率 > 30%)!!
更多详情请戳 这里 。
我是宫水三叶,每天都会分享算法知识,并和大家聊聊近期的所见所闻。
欢迎关注,明天见。