三大排序算法之快排

在上一篇文章中，我对归并排序进行了详细介绍。今天，让我们来探讨另一种经典排序算法——快速排序。

快排是一种广泛采用的排序算法，在多项实验比较中，它平均表现常优于其他排序算法，如归并排序和堆排序。快速排序的核心机制是基于分治策略，通过递归地将数据集分割为较小的子集来实现排序。

该算法执行的关键步骤是区间划分过程：选择一个元素作为枢轴（pivot），将数组重组，所有小于枢轴的元素置于枢轴前，而大于枢轴的元素置于枢轴后。然后，算法递归地在枢轴的两侧子数组上重复这一过程，直至每个子集减少至只含单个元素，完成整体排序。通过这种方式，快速排序能够高效地对数据进行排序。

一、区间划分

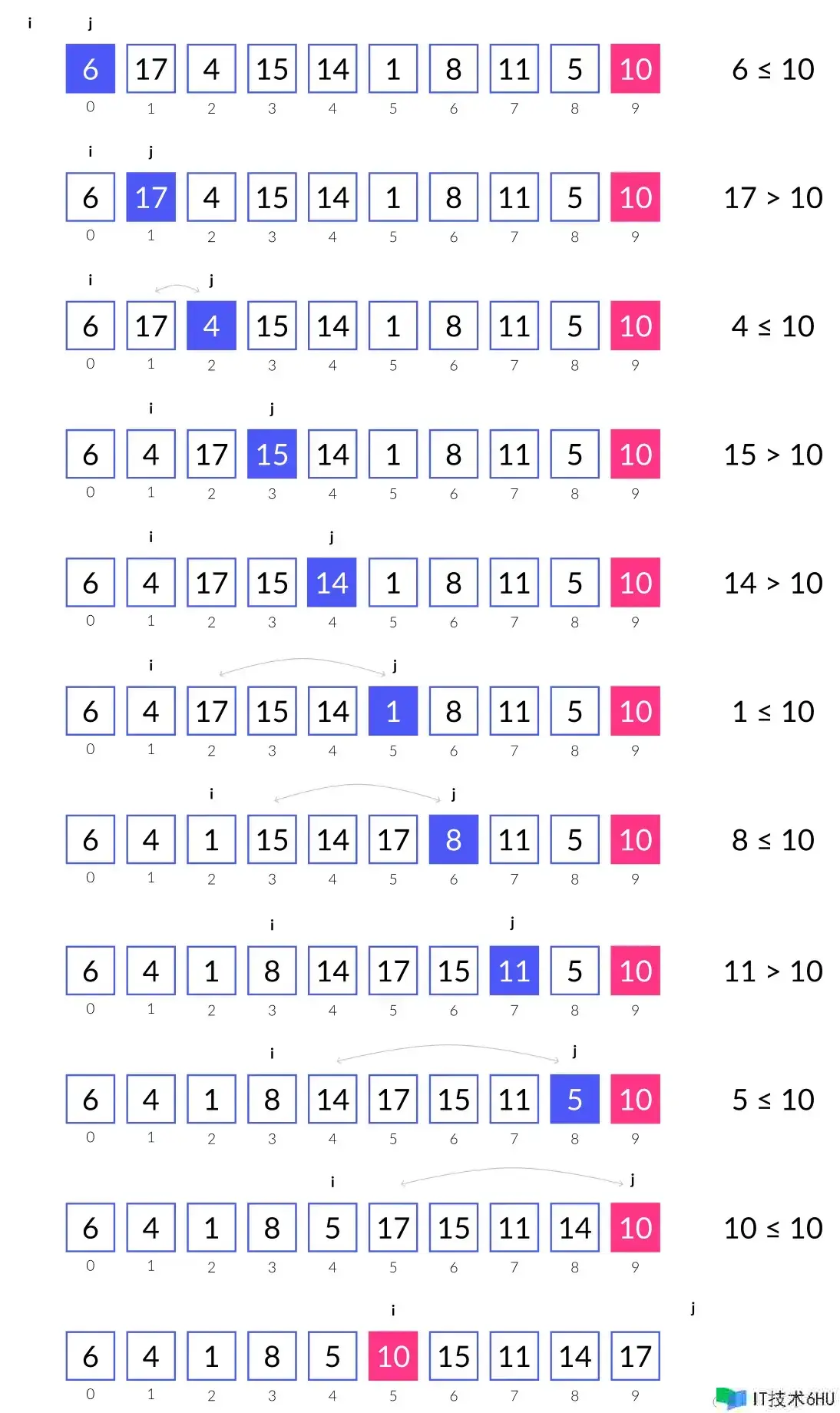
在初始步骤中，我们需要选定一个基准元素，这个元素可以是数组中的任意一项。举例来说，我们选择数组的最后一个元素作为基准。然后进行循环，每次迭代中都会将当前元素与基准进行比较。如果元素小于或等于基准，则它保留在数组的左侧；否则，该元素移至右侧。

我们首先初始化两个指针，$i$ 和 $j$。指针 $j$ 指向数组的第一个元素，而 $i$位于 $j$ 前一位置，即$j-1$。设立这两个指针后，在循环过程中将保持以下的不变性：

• 索引范围 $[left,i]$ 内的元素都不大于基准值。
• 索引范围$[i+1,j)$ 内的元素都大于基准值。

循环完成时，$j$ 将与数组右端对齐，而索引 $i$ 将数组分割为两部分。这些不变性的正确维护确保了数组能够按基准正确划分。

在每次迭代过程中，$j$ 会逐一递增，始终指向当前处理的元素。接着比较当前元素 $array[j]$ 与基准元素 $pivot$。如果当前元素小于或等于基准，则它会与 $i+1$ 位置上的元素进行交换。依据之前提到的不变性，我们可以确定 $array[i+1]$ 的值大于基准元素。因此，小于或等于基准的元素会与大于基准的元素交换位置，实现向左移动。进行这样的交换后，我们的不变性规则被打破。为了修复这一规则，$i$ 的值随后增加 $1$。

当 $array[j]$ 大于基准时，不变性规则依然成立，我们仅需继续到下一次迭代（$i$ 的值保持不变）。

经过所有迭代之后，可以观察到数组会被正确地分区。下述代码片段展示了这一逻辑过程。值得注意的是，这里会返回基准元素的索引位置。

def partition(a, left, right):
    pivot = a[right]
    i = left - 1
    for j in range(left, right + 1):
        if a[j] <= pivot:
            i += 1
            a[i], a[j] = a[j], a[i]
    return i

二、排序过程

排序算法通过递归方法执行。初始步骤中，按照前面的说明，数组被划分为两个部分。对于这两部分中的每一部分，都将重复进行递归的分区过程，直至部分中只剩一个元素需要进行划分。

相关算法的函数实现如下所示。

def quicksort(a, left, right):
    if left < right:
        index = partition(a, left, right)
        quicksort(a, left, index - 1)
        quicksort(a, index + 1, right)

三、复杂度

因为快速排序的精确渐进分析非常详细且复杂，我不想深入讨论所有细节，而是提供一个非正式的证明。

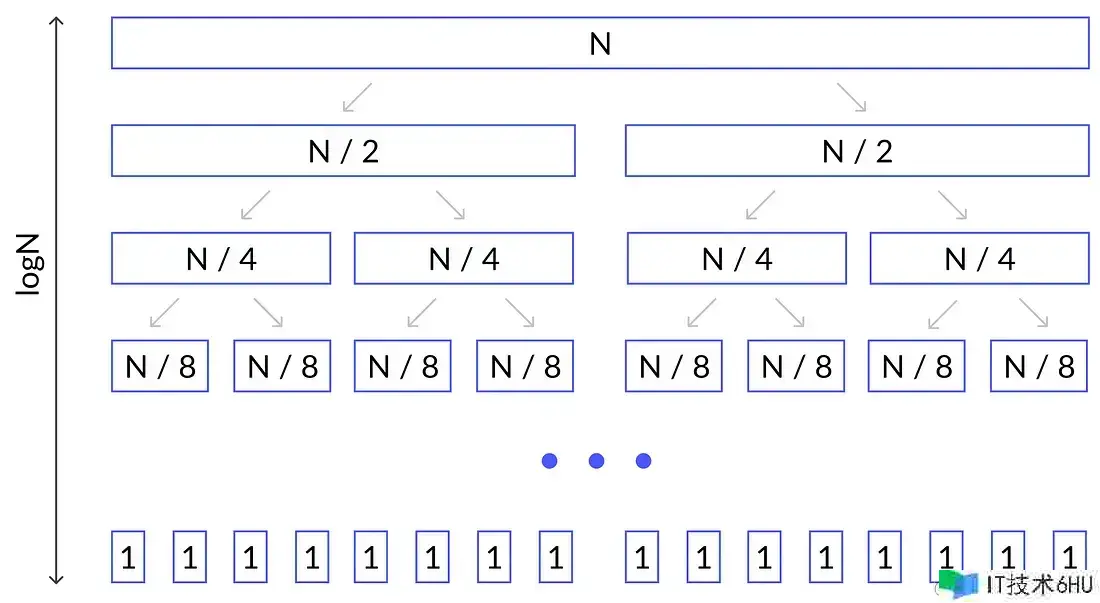
在每次分区操作中，我们会逐个检查数组中的所有元素，这样的操作复杂度为 $O(K)$，其中 $K$ 代表数组的大小。假设每次分区之后，选取的枢轴元素能将数组均匀分成两部分，我们就对这两部分分别递归地进行快速排序，直至数组缩减至仅剩一个元素待排序。这样形成的函数调用结构，与归并排序的结构相似。

区别在于，我们执行的是分区操作而不是合并操作，尽管它们的时间复杂度都为 $O(K)$。考虑到结构的相似性，我们可以推断快速排序的时间复杂度为 $O(N\ast logN)$。归并排序的渐进分析可以查看之前的博文。

在先前的证明中，我们假设了数组被等分为两个部分，但显然这种情况并非总是成立的。假设分区过程总是从其他元素中分离出仅一个元素。那么，在每次迭代中，数组的大小将会是$N-1$、$N-2$、$N-3$、…、直至 $1$，每次都需进行分区操作。我们使用等差数列求和公式来计算这种情况下的总时间复杂度：

T(N)=O(N)+O(N−1)+O(N−2)+O(N−3)+…+O(1)=O(N∗(N+1)/2)=O(N2)T(N) = O(N) + O(N – 1) + O(N – 2) + O(N – 3) + … + O(1) = O(N * (N + 1) / 2) = O(N)T(N)=O(N)+O(N−1)+O(N−2)+O(N−3)+…+O(1)=O(N∗(N+1)/2)=O(N2)

这样，我们得到了二次方的时间复杂度，这是快速排序可能面临的最坏情况。尽管如此，这种情况发生的可能性极低。

通常情况下，快速排序的时间复杂度为 $O(N\ast logN)$，性能优于其他排序算法。

设想你正在开发一个内部使用快速排序算法的系统。总是根据相同的原则选择枢轴元素（例如，在我们的例子中，我们总是选择数组的末尾元素）并不明智。如果有人识破了系统选择枢轴元素的策略，则他可以故意输入会导致最坏分区情况的数组，从而使时间复杂度达到 O(N2)O(N)O(N2)。这可能会显著降低系统的效率。因此，每次迭代最好以不同的方式选择枢轴元素。一个流行的做法是随机选择枢轴元素。

四、结论

快排是一种广泛认可且应用的排序算法。尽管在理论上，在最坏的情况下它可能展现出二次方的时间复杂度，但在实际应用中，特别是当处理大规模数据集时，它通常表现出色，相较于归并排序或堆排序等其他经典算法，快速排序在多数情况下能更有效地处理数据。这种性能优势源自其分而治之的策略，使得它在处理复杂和庞大数据时更为高效和灵活。因此，尽管存在理论上的复杂性峰值，快速排序仍是许多现实场景中的首选排序技术。