神经网络模型

我们在上一篇《神经网络(一) — 数据处理》我们详细唠叨了M-P神经元，M-P神经元它可以同时接受 $x_{1}、x_{2}、x_{i}、x_{n}$ 多个输入信号，这些信号按照 $w_{1} 、w_{2} 、w_{i} 、w_{n}$ 权重与神经元连接，神经元会将输入的信号执行加和操作： $∑1nxiwi=x1w1+x2w2+…+xiwi+xnwnsum_{1}^{n}{x_{i}w_{i}} = x_{1} times w_{1} + x_{2} times w_{2} + … + x_{i} times w_{i} +x_{n} times w_{n}$ 。

输入的公式为： $sum_{i=1}^{n}{w_{i}x_{i}}+b$ ，这里简单的提一下 $b$ ,我们称之为偏置（Bias），用来调整神经元对输入的敏感程度。偏置项会加在输入值上，并且对每个神经元都有一个独立的偏置值。它的作用是在激活函数中引入一定的灵活性，使得神经网络能够学习到更复杂的函数关系。偏置可以理解为一种偏移量，它可以使神经元在输入空间中更灵活地调整位置，从而更好地拟合数据。简单的理解就是b就是一个固定的数字，加权和 + B 趋近阈值才会触发激活函数。

得到加权和后在比对神经元内部的阈值，阈值是指在神经网络的激活函数中，用来判断神经元是否激活的一个界限值。在激活函数中，如果神经元的输入值超过了阈值，神经元就会被激活（输出为1或者对应的激活状态），否则神经元就会保持未激活状态（输出为0或者对应的非激活状态）。在神经网络中，阈值一般是一个固定的常数值，用来控制神经元的激活状态。如果大于阈值，那么就会触发神经元内部的”激活函数”使得神经元处于激活状态。

为了将图片传递给神经元，我们提取了图片像素RGB的值，然后进行了数值的整理以及归一化操作。最终得到了一组符合M-P神经元输入的数据。如果你对这段话有一丁点儿疑惑(除了神经元的激活函数没有提及过之外)，那么接下来的部分不适合你，返回《神经网络(一) — 数据处理》再阅读一边吧！

再次明确目标

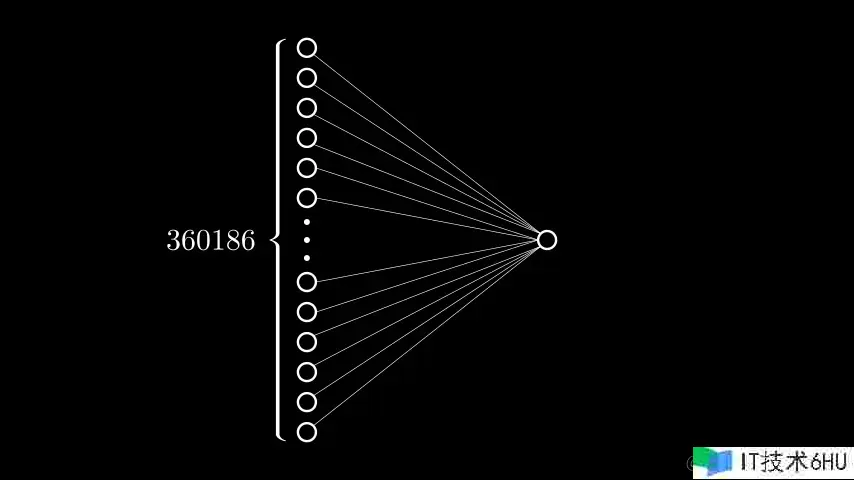
我们的目标是自己设计一个神经网络，将一张凯撒(猩猩)的照片传递给该神经网络后，输出图片的内容是否是猩猩(这是一个典型的分类任务)。先捋一下目前我们有的东西，我们有了一组长度为360186的数据(可以理解为是一个360186维的向量 )。此外我们了解M-P神经元的基本结构。除此之外没有别的了…

构建神经网络模型

如何将360186这么多个数字传给一个神经元呢？所以我们需要有个东西先接收这些数字，以我们现有的东西只有神经元和权重w。w权重只是一个数字，没有办法接收输入值。因此只有神经元可以担当此角色。所以在第一层的神经元主要工作是接收这360186个数字。所以我们需要创建360186 个神经元。此时有些同学在想

虽然看起来比较夸张，第一次就需要这么多的神经元，但是此情此景好像只好如此了，在后面的章节中我们在讨论如何改进它。

接受数据的这一层我们称之为输入层，该层的神经元不做任何的加和操作，也不做与阈值的对比操作，就是单纯的接收输入数据。输入层通过权重w与输出结果神经元相连（当前问题只是简单的二分类问题，所以我们只需要一个神经元表示即可）。那么当前结果神经元所处的层级我们称之为输出层。我们简化神经元内部结构，使用一个圆圈代表，w权重使用一条线代表，可以画出下图：

from manim import *
class Perceptron(Scene):
    def construct(self):
        # 创建16个圆圈，半径为0.5，竖向排列，位置相对圆心点左侧四个单位。
        circles1 = [Circle(radius=0.15, color=WHITE) for _ in range(6)]
        dot = [Dot(radius=0.05, color=WHITE) for _ in range(3)]
        circles2 = [Circle(radius=0.15, color=WHITE) for _ in range(6)]
        # 创建三个dot
        input_level = VGroup(*circles1, *dot, *circles2).arrange(DOWN, buff=0.2).shift(LEFT * 2)
        self.add(input_level)
        # 在input_level左侧添加一个大括号，颜色为黄色 。大括号左侧添加一个数字360186
        input_level_brace_label = BraceLabel(obj=input_level, text="360186", brace_direction=[-1., 0., 0.],
                                             color=WHITE)
        self.add(input_level_brace_label)
        # 创建一个圆圈，半径为0.15，颜色为白色，位置相对圆心点右侧四个单位。
        output_level = Circle(radius=0.15, color=WHITE).shift(RIGHT * 2)
        self.add(output_level)
        # circles1 创建 output_level之间创建连线
        line_group = VGroup()
        for i in circles1:
            temp = Line(i, output_level, color=WHITE, stroke_width=1)
            line_group.add(temp)
        for i in circles2:
            temp = Line(i, output_level, color=WHITE, stroke_width=1)
            line_group.add(temp)
        self.add(line_group)

激活函数

前面提到过，如果某一个神经元的接收的输入值的总和逼近该神经元的阈值，那么这个神经元就会处于兴奋状态。那么这个动作便是“激活函数”的效果。所谓的激活函数本质就是一个数学函数。常见激活函数如下：

Sigmoid函数：将输⼊映射到[0, 1]之间，常⽤于⼆分类问题或者作为输出层的激活函数。
Tanh函数：将输⼊映射到[-1, 1]之间，也常⽤于⼆分类问题或者作为输出层的激活函数。
ReLU函数（Rectified Linear Unit）：将负数输⼊映射为0，保留正数输⼊，常⽤于隐藏层的激活函数
Softmax函数：将输⼊映射为概率分布（输出的向量的每⼀个值都为正⽽且元素之和为⼀）。常⽤于多分类问题的输出层。

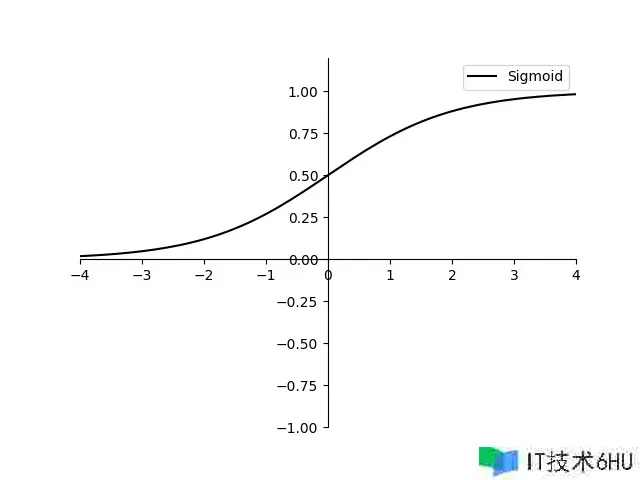
暂时不需要完全搞明白每个函数的意义，后面的章节我会一步一步带领大家认识他们。目前先认识一下SIgmoid函数：

import math
import numpy as np
import matplotlib.pyplot as plt
from PIL import Image
# set x's range
x = np.arange(-10, 10, 0.1)
y1 = 1 / (1 + math.e ** (-x))  # sigmoid
# y11=math.e**(-x)/((1+math.e**(-x))**2)
y11 = 1 / (2 + math.e ** (-x)+ math.e ** (x))  # sigmoid的导数
y2 = (math.e ** (x) - math.e ** (-x)) / (math.e ** (x) + math.e ** (-x))  # tanh
y22 = 1-y2*y2  # tanh函数的导数
y3 = np.where(x < 0, 0, x)  # relu
y33 = np.where(x < 0, 0, 1)  # ReLU函数导数
plt.xlim(-4, 4)
plt.ylim(-1, 1.2)
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.spines['bottom'].set_position(('data', 0))
ax.spines['left'].set_position(('data', 0))
# Draw pic
plt.plot(x, y1, label='Sigmoid', linestyle="-", color="black")
# plt.plot(x, y11, label='Sigmoid derivative', linestyle="-", color="blue")
#plt.plot(x, y2, label='Tanh', linestyle="-", color="black")
#plt.plot(x, y22, label='Tanh derivative', linestyle="-", color="blue")
#plt.plot(x, y3, label='Tanh', linestyle="-", color="black")
#plt.plot(x, y33, label='Tanh derivative', linestyle="-", color="blue")
# Title
plt.legend(['Sigmoid', 'Tanh', 'Relu'])
plt.legend(['Sigmoid', 'Sigmoid derivative'])  # y1 y11
#plt.legend(['Tanh', 'Tanh derivative'])  # y2 y22
#plt.legend(['Relu', 'Relu derivative'])  # y3 y33
#plt.legend(['Sigmoid', 'Sigmoid derivative', 'Relu', 'Relu derivative', 'Tanh', 'Tanh derivative'])  # y3 y33
# plt.legend(loc='upper left')  # 将图例放在左上角
# save pic
# plt.savefig('plot_test.png', dpi=100)
plt.savefig(r"./")
# show it!!
plt.show()

现在大家只需要记住他有两个特点：

它能将输入的任何数值都映射到0到1之间的数值。
它是一个连续可导的函数，这一点在函数反向求导时非常重要；

每个神经元接收的数据 $∑1nxiwi=x1w1+x2w2+…+xiwi+xnwnsum_{1}^{n}{x_{i}w_{i}} = x_{1} times w_{1} + x_{2} times w_{2} + … + x_{i} times w_{i} +x_{n} times w_{n}$ ，最终我们得出的是一个数字(与阈值的比对后也是一个数字)。但是这个数字等于什么的时候，我们才能认定这张图片是猩猩呢？我们希望最终得到的结果是一个百分比数值，那么我们就可以很好的判断出图片是否是猩猩。百分比的数值恰好在【0，1】的范围，sigmoid函数的特点正好配！！！！

停下来我们捋一下步骤，首先我们创建了两层的神经网络，输入层接收外界信号后传输给输出层，输出层是M-P神经元(这里也可以称之为“阈值逻辑单元”)

小贴士：两层的神经网络有一个比较明显的特点，他更能容易的实现逻辑与、或、非运算。一般应用在隐藏层，也可以用在输出层。此外这种特点的网络我们也可以称之为感知机。

输出层接收到输入数据后会触发激活函数，如果选取的激活函数是sigmoid函数，那么此神经元最终输出的结果属于【0，1】的结果值。如果结果趋近于1，那么可以认为图片中的动物就是猩猩。

小贴士：激活函数引⼊了⾮线性操作，使得神经⽹络可以更好地拟合复杂的⾮线性关系。如果神经⽹络只使⽤线性激活函数，那么整个⽹络将只是多个线性操作的组合，⽆法处理⾮线性数据或者学习⾮线性映射。神经元的输出可以作为后续神经元的输⼊，从⽽构成了神经⽹络的层次结构。通过在神经⽹络中连接⼤量的神经元，并通过训练来优化神经元之间的连接权重，⼈⼯神经⽹络可以在⼤量数据上进⾏学习和预测，⼴泛应⽤于机器学习和深度学习任务，如图像识别、语⾳识别、⾃然语⾔处理等。

权重参数与阈值

输入的值有了(图片向量)，输出的方式有了(sigmoid函数)。那么就差一系列的和输出层神经元的阈值。按照设计的网络模型，有多少输入值就应该有多少的权重。每个人输入的权重值应该各不相同。那么如此多的权重参数我们如何得之呢？

有一个简单的方式，那就是随机！！！我们为每个输入都随机的赋上一个权重参数。很多同学可能会想到，这么随意，模型最终的效果会好么？答案是肯定的，一定会很差。但是模型在不断的学习训练过程中会不断的更新调整这个权重参数。最终我们会得到一组完美的权重参数。也就标志着模型已经训练完毕了。那么如何调整，如何优化我们后续章节会讲到。

模型预测

输入层数据：[0.9937,0.9937,0.9937,0.9937,0.9937,0.9937,−1.0787,−1.1091,−1.1394,…,…,…,−1.0695,−1.0999,−1.1292]

权重参数(随机)：【0.14 , 1, -0.13, -0.6, -0.88, 0.33 ,…,…,…, 0.12, 0.3, 0.1, 0, -0.01, 0.1 】

偏置参数(固定)：0.2

输出神经元阈值 : 0.5

输出的激活函数：sigmoid函数

请大家记住，这里只是为了直观的体现计算过程，其实当前向量中有360186个数字。我们只是吧第一个、第二个以及第360185个、第360186个像素拿出来举例！！！！。

$∑1nxiwi=x1w1+x2w2+…+xiwi+xnwn=−0.5802629999999998sum_{1}^{n}{x_{i}w_{i}} = x_{1} times w_{1} + x_{2} times w_{2} + … + x_{i} times w_{i} +x_{n} times w_{n} = -0.5802629999999998$

$sum_{i=1}^{n}{w_{i}x_{i}}+b= -0.5802629999999998 + 0.2 = -0.3802629999999998$

$frac{1}{1+e^{-left( -0.3802629999999998 – 0.5 right) }} approx 0.2931232818094643$

也就是说当前预测图片中的动物是否是猩猩的百分比是29.3%。所以当前模型还未达到理想的状态，换句话说我们随机初始化的权重参数或者是偏置参数还需要不断的优化(阈值的取值在不同的场景中有不同的取值。通常二分类问题阈值初始状态一般为0.5)。

多层神经网络

模型的效果差固然与权重参数与阈值有关系，但是由于权重参数过于庞大，尚且不知道如何调优，那么有没有别的方案可以不用调节权重参数与阈值的前提下可以让效果好一些呢？

大家有没有想过上述的两层神经网络的学习能力有限，除了体现在随机的权重参数，阈值。有没有可能是神经元的个数或者是网络结果的层数有关系。因为在我们生物学中的神经网络中可是要比上述的模型复杂的多。所以我们需要对上述的模型进行优化：

from manim import *
class MultiLayer(Scene):
    def construct(self):
        # 创建16个圆圈，半径为0.5，竖向排列，位置相对圆心点左侧四个单位。
        circles1 = [Circle(radius=0.15, color=WHITE) for _ in range(6)]
        dot = [Dot(radius=0.05, color=WHITE) for _ in range(3)]
        circles2 = [Circle(radius=0.15, color=WHITE) for _ in range(6)]
        # 创建三个dot
        input_level = VGroup(*circles1, *dot, *circles2).arrange(DOWN, buff=0.2).shift(LEFT * 3)
        self.add(input_level)
        # 在input_level左侧添加一个大括号，颜色为黄色 。大括号左侧添加一个数字360186
        input_level_brace_label = BraceLabel(obj=input_level, text="360186", brace_direction=[-1., 0., 0.],
                                             color=WHITE)
        self.add(input_level_brace_label)
        #创建隐层6个神经元
        hidden_layer_circles = [Circle(radius=0.15, color=WHITE) for _ in range(6)]
        input_level = VGroup(*hidden_layer_circles).arrange(DOWN, buff=0.2)
        self.add(input_level)
        # 创建一个圆圈，半径为0.15，颜色为白色，位置相对圆心点右侧四个单位。
        output_level = Circle(radius=0.15, color=WHITE).shift(RIGHT * 3)
        self.add(output_level)
        # circles1 创建 output_level之间创建连线
        line_group = VGroup()
        for i in circles1:
            for j in hidden_layer_circles:
                temp = Line(i, j, color=WHITE, stroke_width=1)
                line_group.add(temp)
        for i in circles2:
            for j in hidden_layer_circles:
                temp = Line(i, j, color=WHITE, stroke_width=1)
                line_group.add(temp)
        for i in hidden_layer_circles:
            temp = Line(i, output_level, color=WHITE, stroke_width=1)
            line_group.add(temp)
        self.add(line_group)

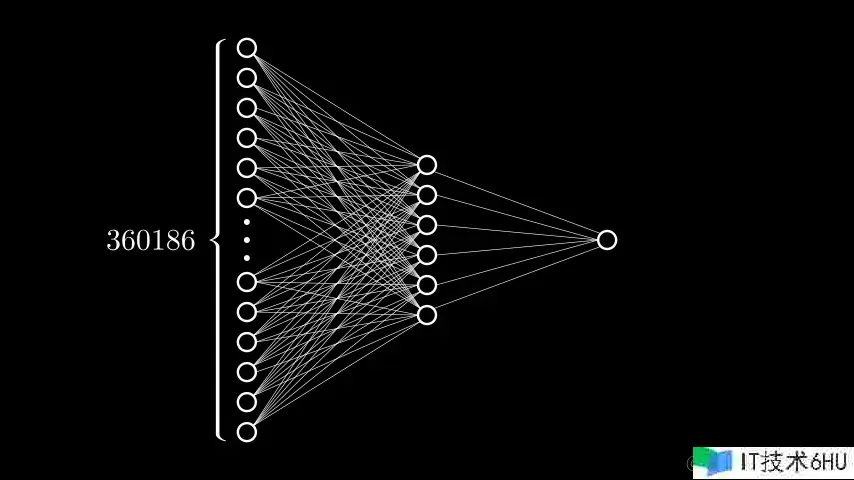
我们在上述两层的网络中又加了一层神经元(中间的六个神经元)，通常我们称之为隐层。说到隐层我们我们需要先搞定什么是隐层，隐层能做什么两个问题。

什么是隐层

在⼈⼯神经⽹络 ANN中，隐层（Hidden Layer）是位于输⼊层和输出层之间的⼀层或多层神经元的集合。作为神经⽹络中的中间层，隐层负责对输⼊数据进⾏特征提取和转换，从⽽实现复杂的⾮线性映射关系。

我们做了⼀个⾮常随意的设定：在输⼊层和中间层之间，加⼊1个隐层（Hidden Layer)。每⼀个隐层有6个神经元，然后我们让每层的每⼀个神经元都和上⼀层的所有神经元都相连，就形成了如图的⽹状结构。如果两层之间，每层的每⼀个神经元都和另⼀层的所有神经元都相连，那么我们便称之为“全连接层”（Fully Connected Layer）。后⾯我们还会陆陆续续认识卷积层、池化层、循环层、嵌⼊层和规范化层，全连接层是我们我们认识的第⼀个神经⽹络的层！
图中这么多的线，每⼀条都代表了⼀个权重，⼀共36.1866+61=2,161,122个权重参数！
图中算上输⼊层共有7个神经元，所以⼀共有7个偏置参数！
上述的这2,161,122+7个参数，在最开始都是随机初始化的，最终他们是神经⽹络在训练过程中，由模型⾃动学习得到的，⽽不是⼈为设置的。对于这些参数，我们称之为“模型参数（Model Parameters）”。与模型参数相对的是“超参数”，后⾯会讲！

隐层能做什么

我们希望隐层能够对输⼊的数据进⾏特征提取和转换，从⽽实现复杂的⾮线性映射关系。我们可能认为，⼈之所以可以认识猩猩，是因为猩猩的鼻子、眼睛、嘴巴、手指等和人类差不多，为数不多的不同就是猩猩的毛发黑而茂盛。那如果要让机器去认识，是不是也能让机器去识别、提取出这些特征呢？理想情况下，我们希望隐层可以先识别出鼻子、眼睛、嘴巴、手指、毛发这些特征，输出层对他们进⾏组装，从⽽知道这是不是只猩猩。

小贴士：常见的多层网络模型并不止一层隐层，两层、三层甚至更多的层数是比较常见的。因为隐层越多，模型对物体的特征描述就越详细，但随之而来的问题就是会导致过拟合。

隐层的存在使得神经⽹络具有强⼤的表达能⼒，能够处理复杂的⾮线性关系，并从输⼊数据中⾃动提取有⽤的特征。隐层的神经元数量、激活函数的选择以及层次结构的设计等因素都会对神经⽹络的性能和学习能⼒产⽣影响，因此在设计和训练神经⽹络时，隐层的设置通常需要经验和调优。

模型预测

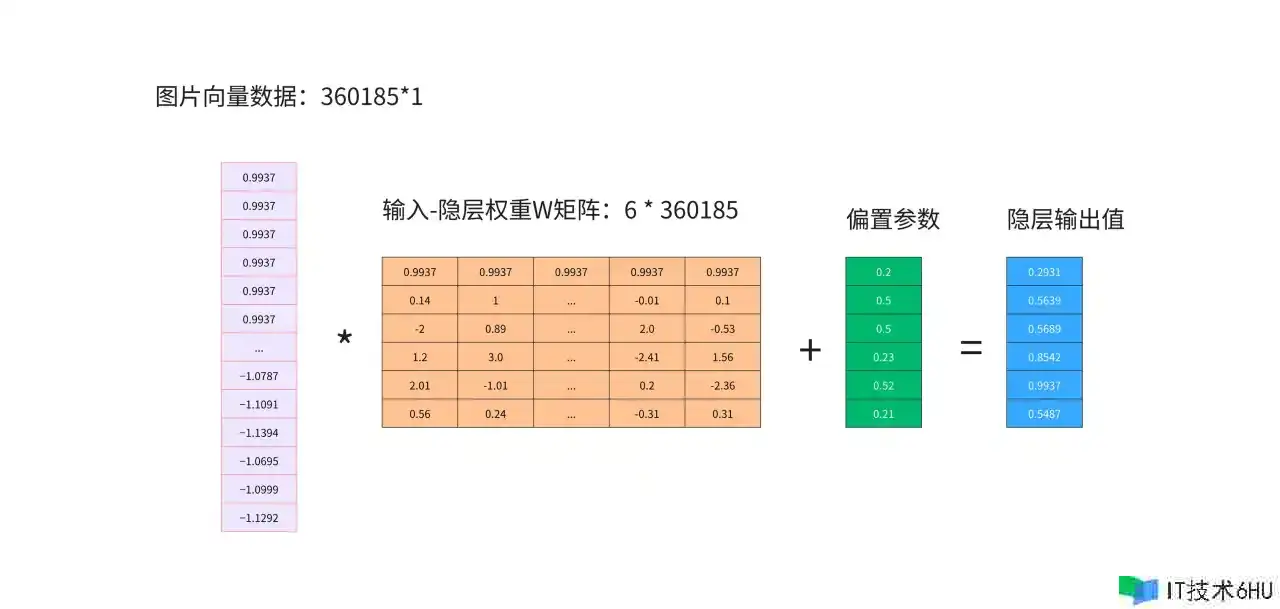
两层网络中输入层直接与输出层的一个神经元相连，而在多层网络中，输入层与隐层相连，隐层与输出层相连。隐层有6个神经元，输入层360185个神经元分别要与隐层中每一个神经元相连。所以我们需要6组隐层权重值。为了方便计算，我们将图片向量与权重参数使用矩阵的方式表示。

隐层的输出即当作输入，在以同样的方式传递给结果层神经元。

至此整个步骤如下：

输入数据—>输入-隐层w权重参数 —>隐层偏置参数—>隐层激活函数(sigmoid函数) —>隐层输出结果(下一层的输入)—>隐层-输出层w权重参数 —>输出层偏置参数—>输出层激活函数(sigmoid函数) —>输出最终结果

前向传播

介绍完神经⽹络的⼤致结构，我们就已经对前向传播这件事有⼀定的了解了！⼀张图⽚变成360185维向量输⼊给神经⽹络的输⼊层的360185个神经元们，⽽后接下来的第⼀层隐层根据它的3601856个权重和6个偏置，产⽣了6个新的输出，送给了下⼀个输出层；最后，输出层在根据⾃⼰的16个权重和1个偏置，输出1个数字。在神经⽹络的设计中，我们往往希望输出层输出的是⼀个概率分布函数，每个值都为正，⽽总和为1（这就 是⼀个Softmax层可以做的！ ）；然后对于值越大就是概率越大。这就是我们的输出。这就是前向传播！

前向传播（Forward Propagation）是⼀种在神经⽹络中进⾏信息传递的过程，它是神经⽹络训练的第⼀步。在前向传播中，输⼊数据通过神经⽹络的多个层（包括输⼊层、隐藏层和输出层）按照预定的权重和偏置进⾏计算，从输⼊层传递到输出层，最终得到神经⽹络的预测结果。

神经网络(二) — 前向传播

神经网络模型

再次明确目标

构建神经网络模型

激活函数

权重参数与阈值

模型预测

多层神经网络

什么是隐层

隐层能做什么

模型预测

前向传播

作者信息

神经网络(二) — 前向传播

神经网络模型

再次明确目标

构建神经网络模型

激活函数

权重参数与阈值

模型预测

多层神经网络

什么是隐层

隐层能做什么

模型预测

前向传播

相关文章

前端录屏+定位源码，帮你快速定位线上bug

快收藏！超强图解Docker常见命令与实战！

一个普通玩家的思考：我们离元宇宙还有多远？

修复Flutter官方Slider bug并成功合入的经历

作者信息