试玩 RealityComposerPro 中的 Shader Graph：用圆环制作一个 Meta Logo

说明

以前在写核算几何时，写到过 S04E11：李萨如曲线体网格生成，其中在一个圆环上叠加 2 个周期的正弦动摇（即 2*2），即可生成 Meta Logo 的 Mesh 网格几何体。

实际上，借用同样的思路只用编写 Shader，也能将一个圆环变成一个 Meta Logo。刚好此次 Xcode 15 中的 Reality Composer Pro 支撑了 Shader Graph 功能，让咱们能够通过拖拖拽拽就能编写好一个 Shader，那就来试玩一下吧！

准备作业

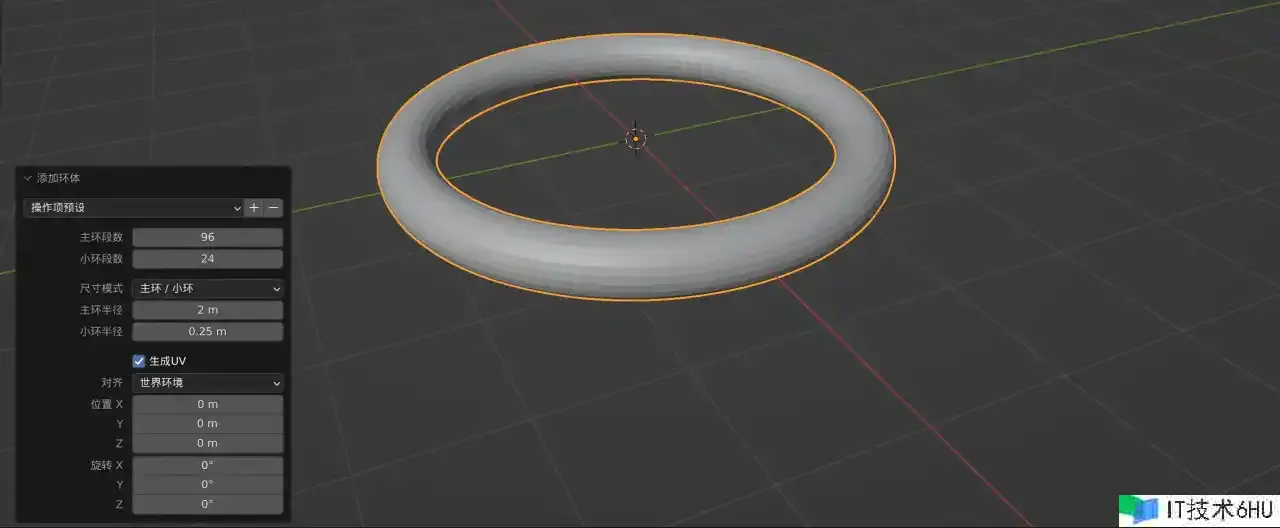
不过首先，咱们需求一个圆环体，这儿不得不吐槽一下，以前在 SceneKit 编辑器界面能够直接拖拽生成圆环体的，现在 Reality Composer Pro 却只有立方体球体等几种。这儿不得不凭借 Blender 生成一下基础的圆环体，记住将主环段数设置的略微大一些，这样变形后的几何体也会平滑。导出为 .usdc 文件即可。

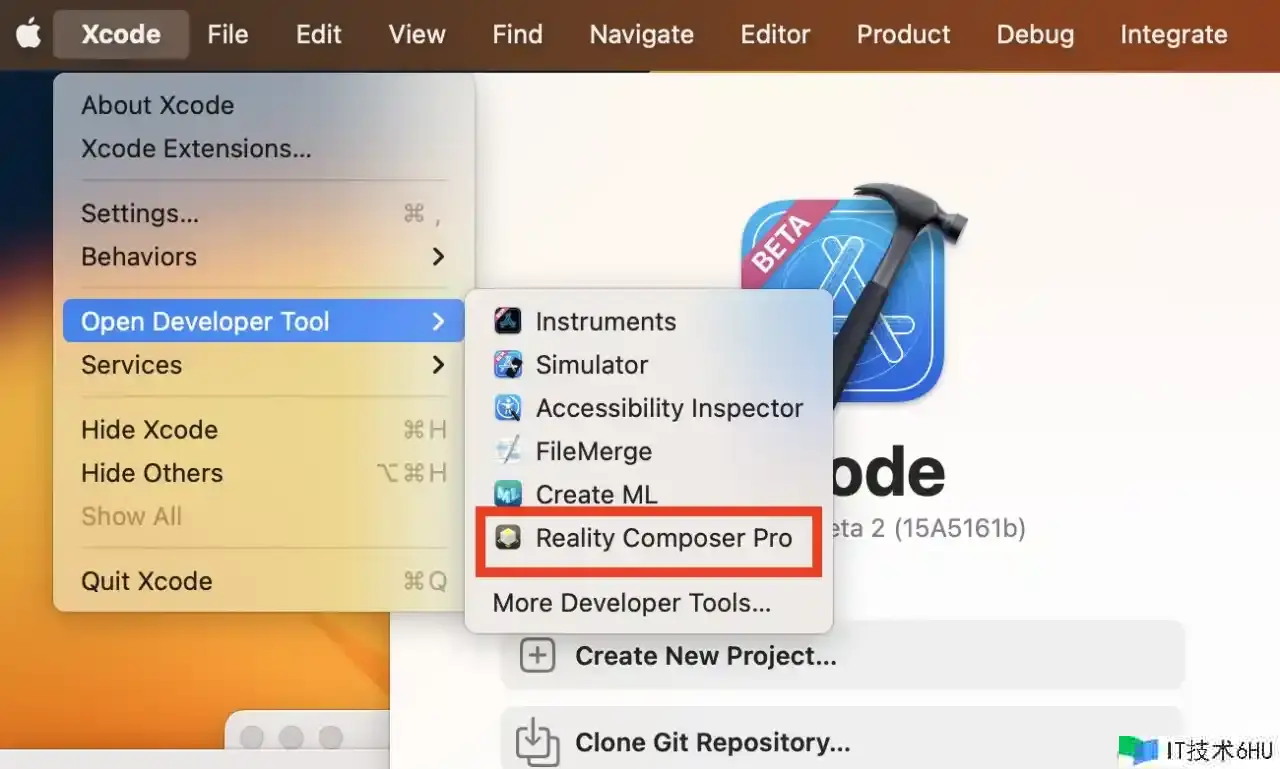
在 Xcode 中翻开 Reality Composer Pro，创立一个新的工程。

将模型导入，并拖动到 3D 场景中，由于没有原料，所以整个模型显现为紫赤色条纹，咱们需求创立一个新的原料。

将原料应用到圆环几何体上，然后选中原料，翻开 Shader Graph 面板，能够愉快地编写 Shader 了。

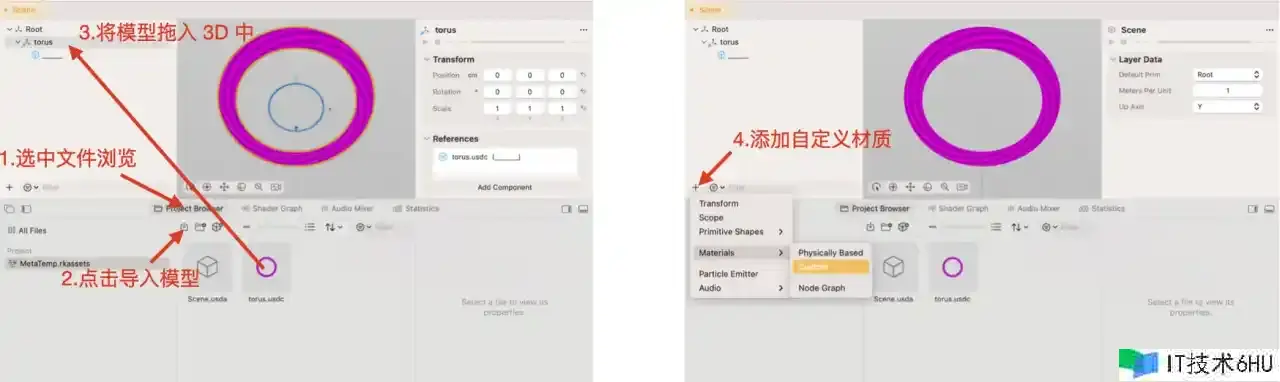
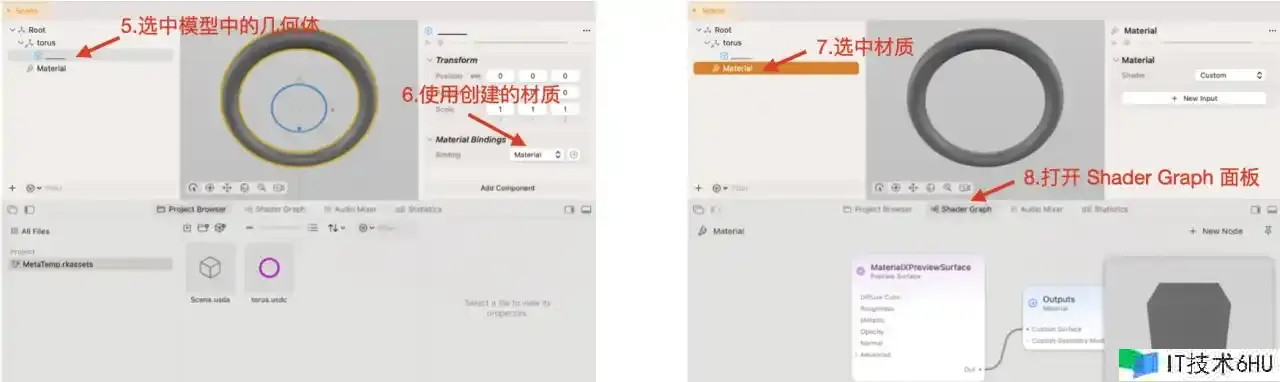
增加新的 Shader 节点的办法是：在空白处双击，或从任一输入或输出拖拽出来，即可弹出挑选面板。引荐选用拖拽方法，由于这样能够主动匹配类型，比方从输出拖拽时，输出类型是 vector3 的话，弹出界面中会筛选出能够承受 vector3 类型的节点。

别的需求提前留意的是：圆环模型大环在 XY 平面上，半径 2m，小环是绕 Z 轴旋转，半径 0.25m。要得到 Meta Logo 咱们需求编写 Shader 将圆环上的点沿 Z 轴进行偏移。

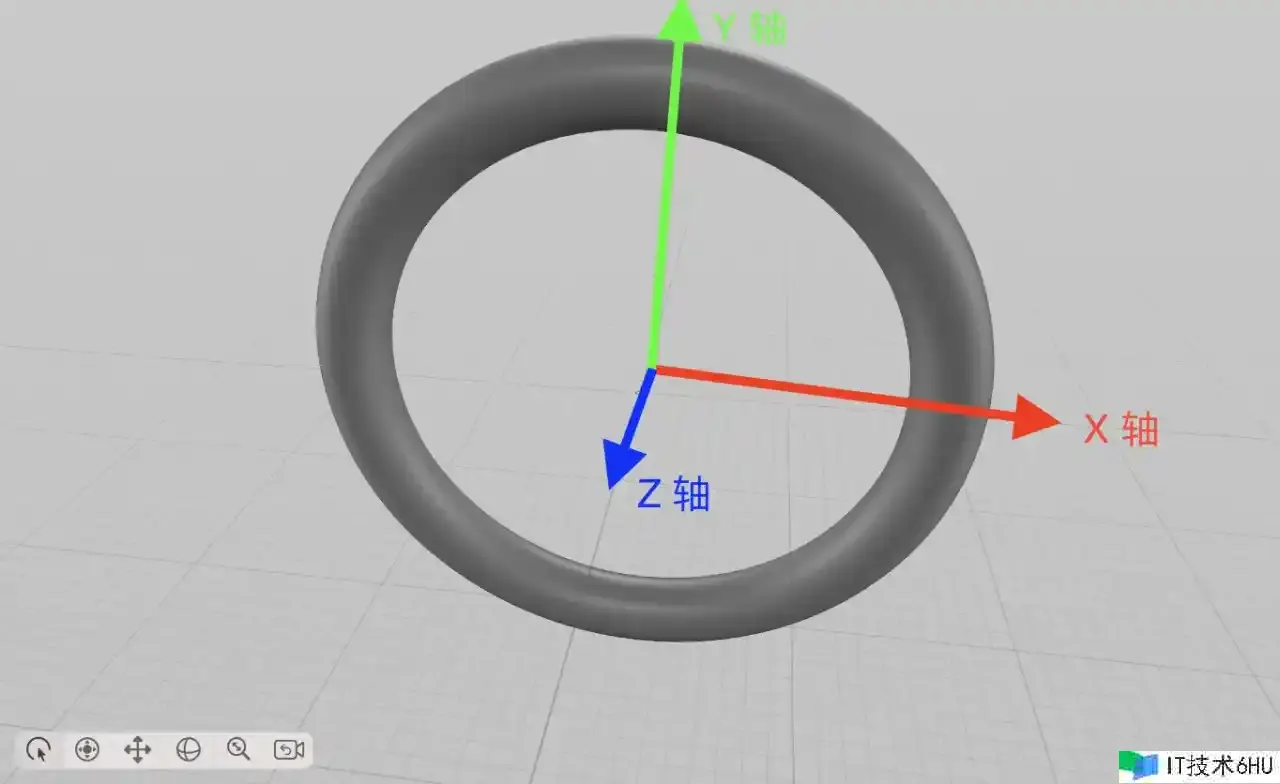
基本思路

假如直接对一切点沿着 Z 轴进行偏移的话，由于不同方位的偏移量不一致，会导致圆环变得扁平。

这时咱们就需求先沿旧法线将小环收缩成一条线并增加 Z 坐标歪曲，然后从头核算歪曲后的法线，再沿新的法线康复小环，就能让小环康复成圆形。全体流程和作用如下图所示：

接下来，咱们依照五个主要流程来解说核算的原理。

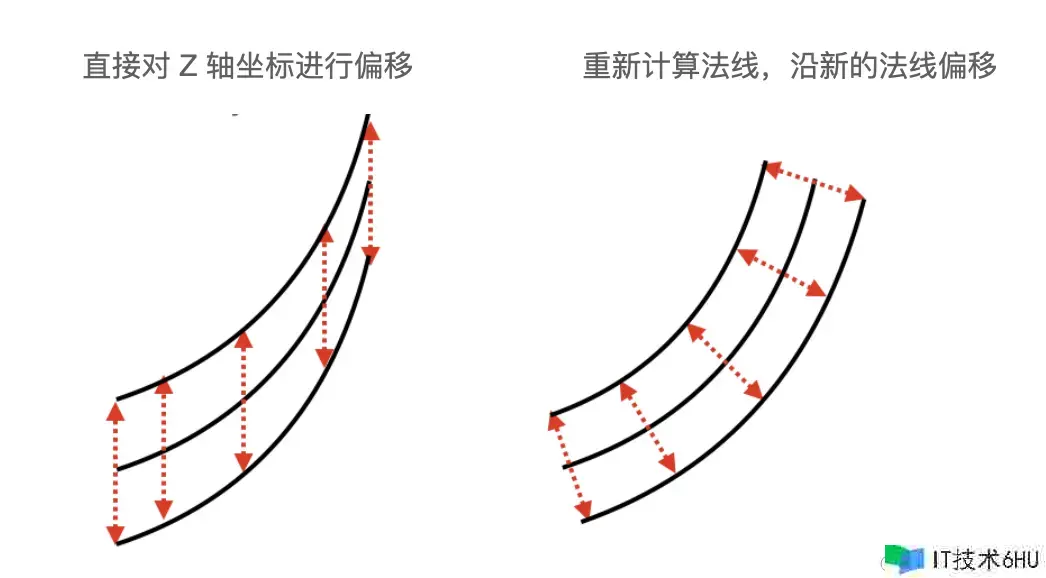
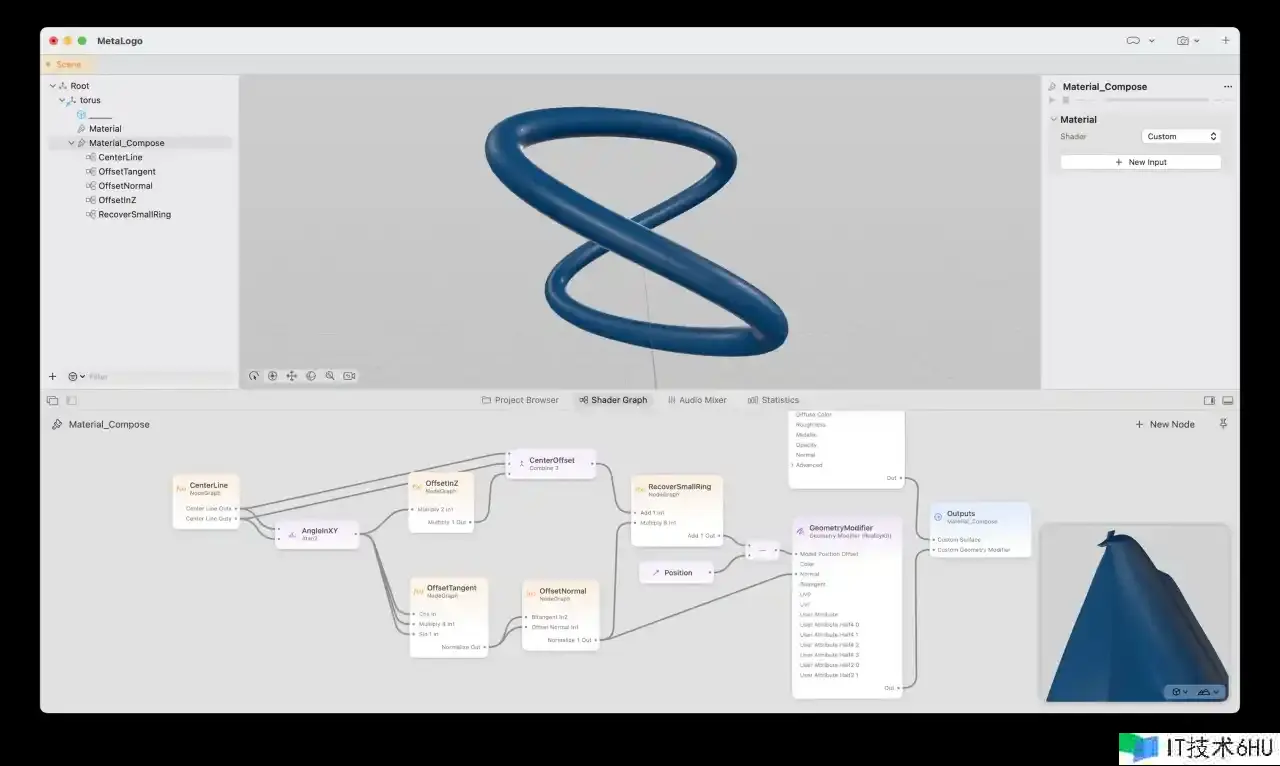
1.收缩小环

要收缩小环其实十分简单，增加一个 GeometryModifier，然后将一切的点沿法线移动 -0.25，即可将小环缩小到 0。用伪代码表达：

newPosition =  position + normal * (-0.25)

当然，假如此时直接缩小到 0 就看不到，为了便利调查能够先移动 -0.245

可是，由于最终回来的是偏移量 Position Offset，也便是将原有的点移动多少而不是每个点的具体方位，这样会导致后续核算呈现困难，所以咱们还需求做一些小的修正：先加上原始方位，得到偏移后的坐标，中间核算能够在此基础上进行，最终输出时再减去原始方位，得到最终偏移量做为输出。

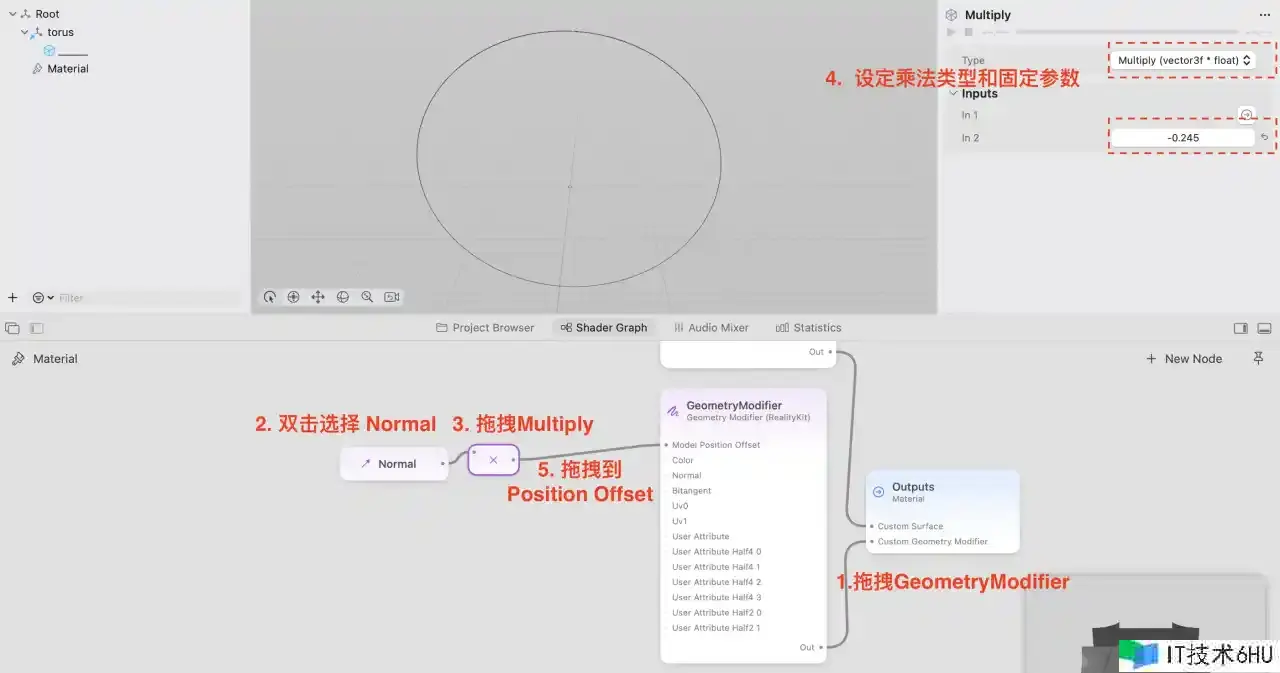
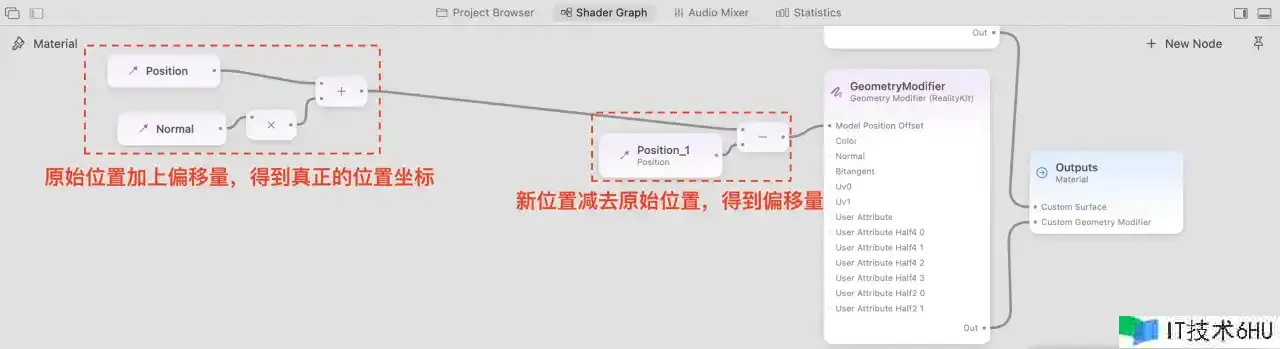
由于鄙人一步中，咱们需求对 Z 坐标进行独自操作，这时咱们就需求用到别的两个节点：Separate3 和 Combine3，前者能够将三维向量分解为三个独自的量，后者则是将三个独自的量组合为一个三维向量。

选中前面多个节点，点击右键，挑选：Compose Node Graph 来紧缩节点收拾一下，将紧缩后的命名为：CenterLine。至此，收缩小环的作业完美完成了！

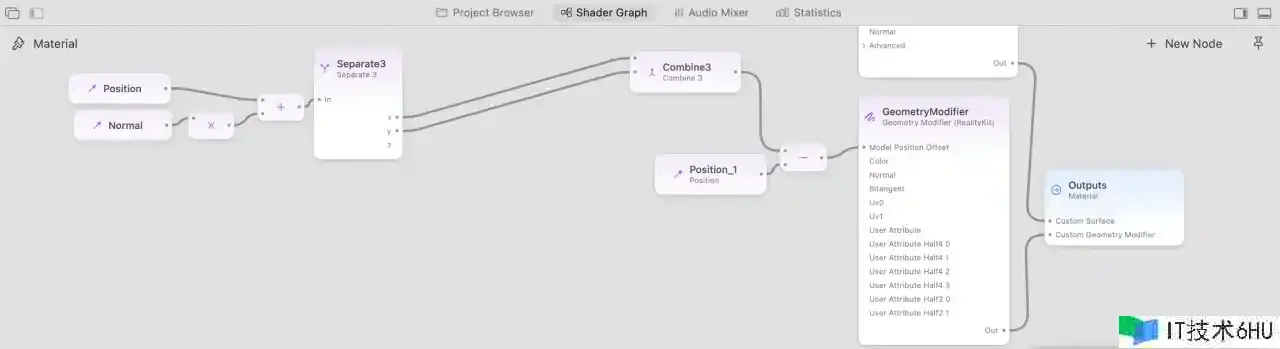
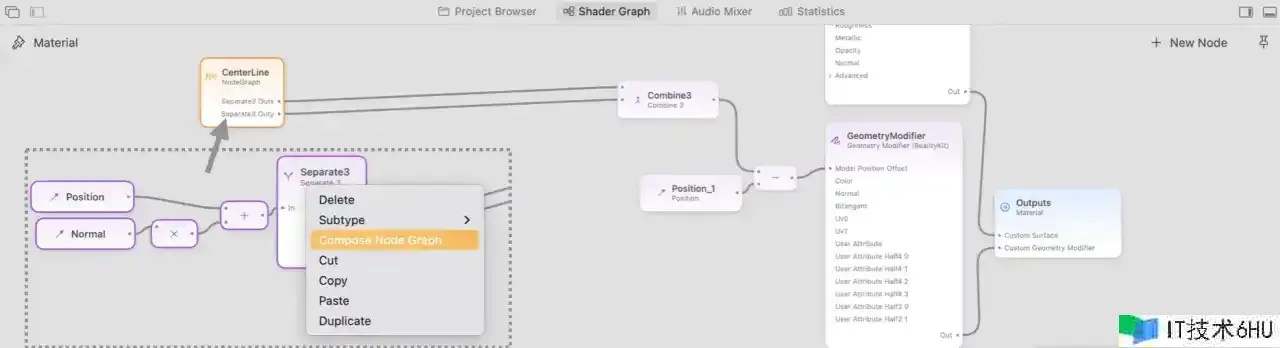
2.歪曲大环

要歪曲大环，咱们需求知道每一个点在大环上的方位，或者说视点。这儿咱们使用 atan2 函数来求夹角，将 XY 坐标输入就得到该点相对于 X 轴的夹角，输出范围为 (-,]。

接下来对 Z 坐标增加 2 个周期的歪曲，动摇起伏也是 2m，用伪代码表达便是：

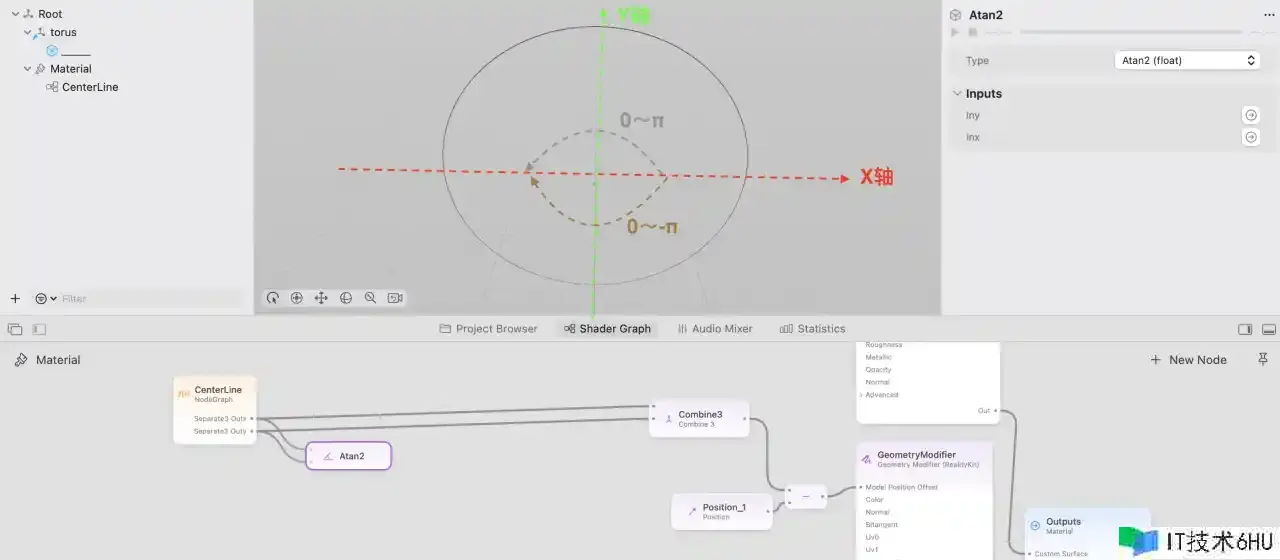
angle = atan2(x, y)
z = sin(2*angle) * 2

能够看到大环发生了明显的歪曲，滚动不同方位调查，就会发现已经和 Meta Logo 比较相似了。

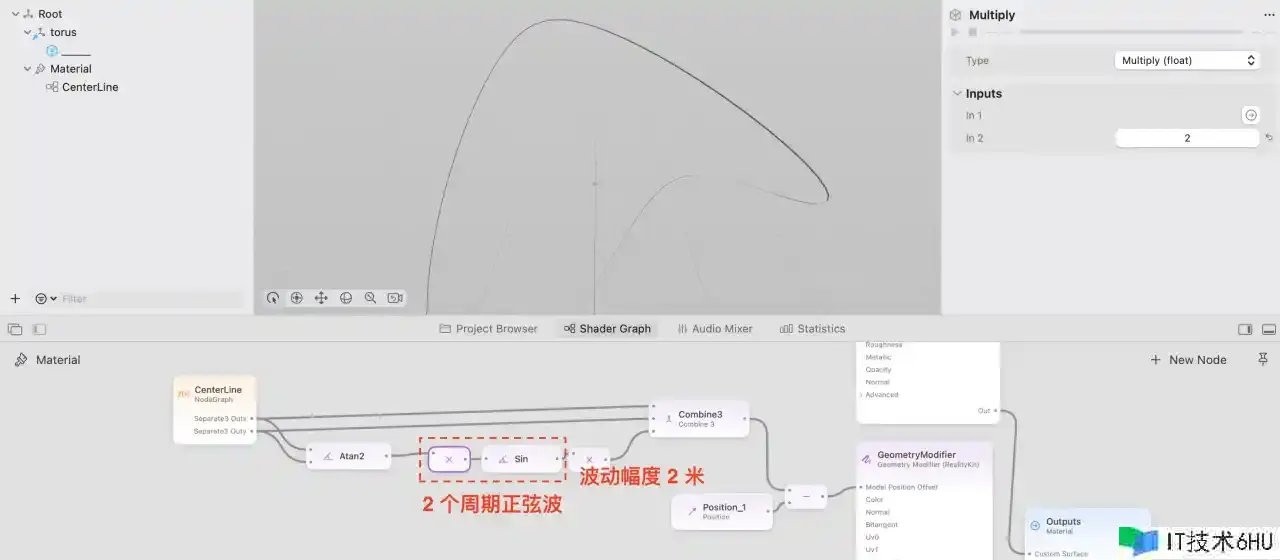
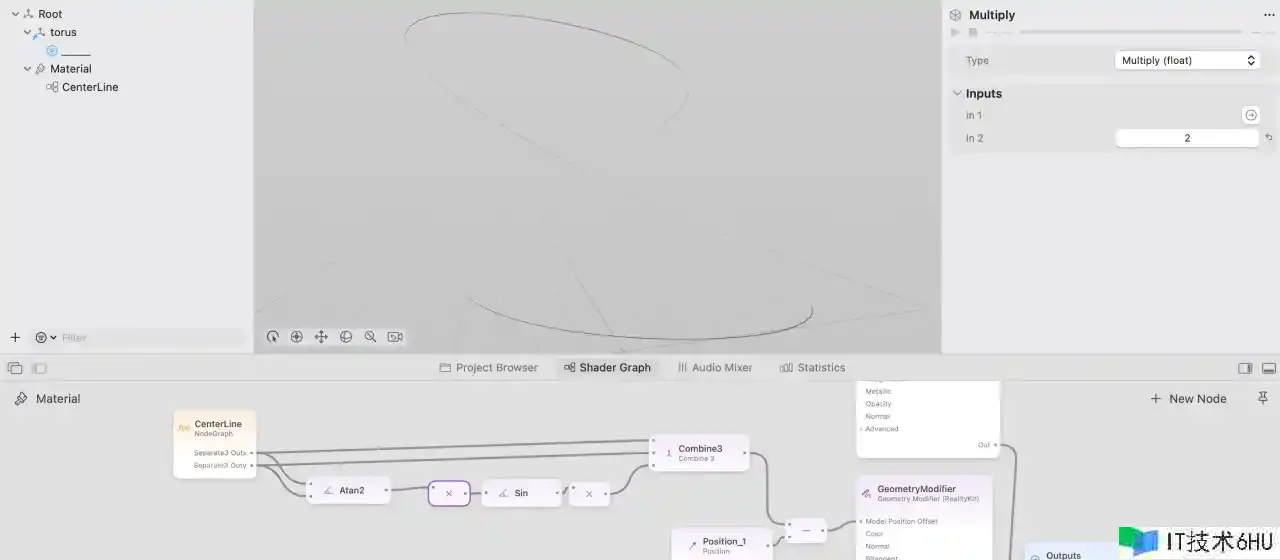
3.核算歪曲切线

要获取歪曲后的法线，需求先核算歪曲后大环的切线。这儿咱们弥补一点数学知识：假如已知一条曲线的数学表达式，要求恣意点的切线，只需求对其表达式求导即可。那么收缩后的图形的表达式为：

// 大环半径为 2 米
x = sin(angle) * 2
y = cos(angle) * 2
z = sin(2*angle) * 2
//对其求导后
x' = cos(angle)
y' = -sin(angle)
z' = cos(2*angle) * 2 //复合函数求导链式规律：f[(g(x))]' = f'[g(x)] * g'(x)，也便是说：sin'(2x) = cos(2x) * 2；sin'(3x) = cos(3x) * 3；sin'(4x) = cos(4x) * 4

最终要对求出的切线长度进行归一化 Normalize，以便后续处理，顺便将节点收拾紧缩一下，如下图：

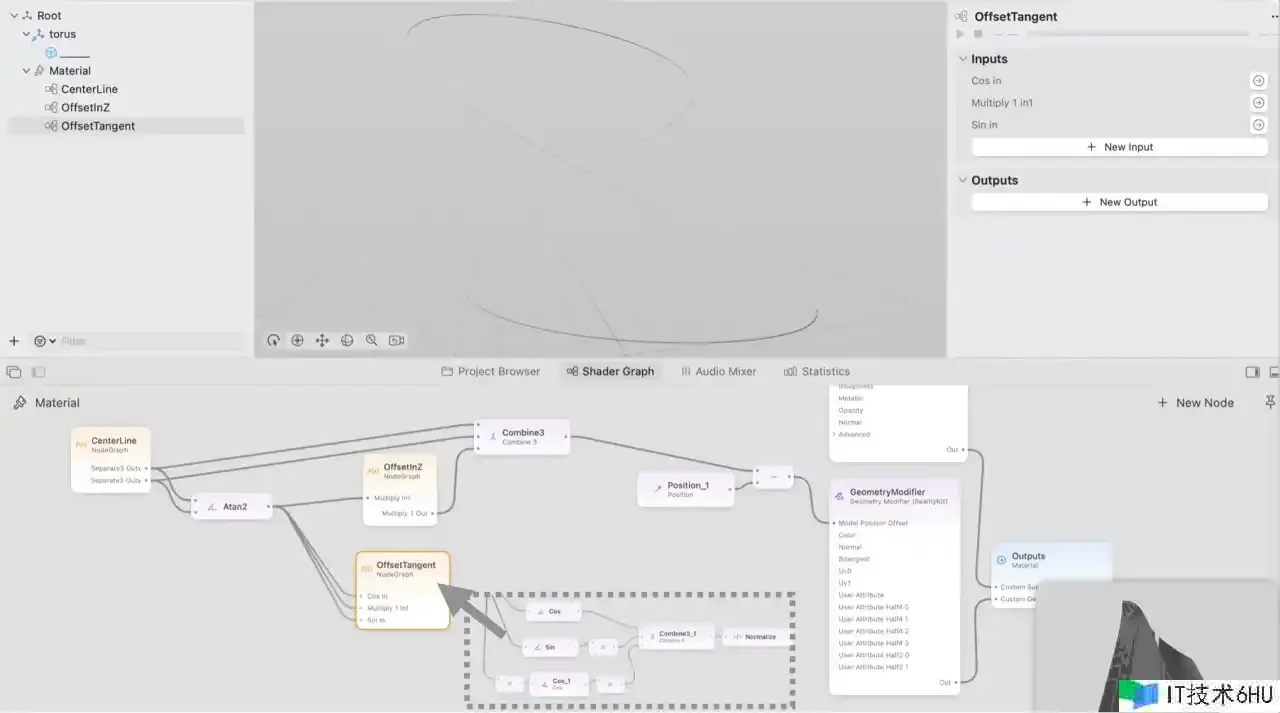
4.核算歪曲法线

咱们先用切线和旧的法线，进行叉乘得到副切线。将副切线与切线再次进行叉乘，即可得到新的法线方向。这儿需求副切线，是由于咱们歪曲 Z 坐标时，副切线不变，它实际相当于旋转轴。

这儿需求留意叉乘的次序：叉乘遵守右手螺旋规律，右手手指从第一个向量动身，向第二个向量弯曲，大拇指方向便是新向量的方向。用伪代码表明如下：

bitangent = cross(tangent, oldNormal)
newNormal = cross(bitangent, tangent)

修正 Shader Graph 如下，最终记住将求出的新法线，赋值给 GeometryModifier 的 Normal 属性，以便显现出正确的光照作用。

5.康复小环

康复小环也很简单，将挤在中心线上的点沿新的法线移动 0.25 米即可，用伪代码表达：

newPosition = centerOffset + newNormal * 0.25

还要记住，将前面的 -0.245 改为 -0.25，以便取得更完美的作用。收拾好的 Shader Graph 如下：

展开后完全版 Shader Graph 如下：

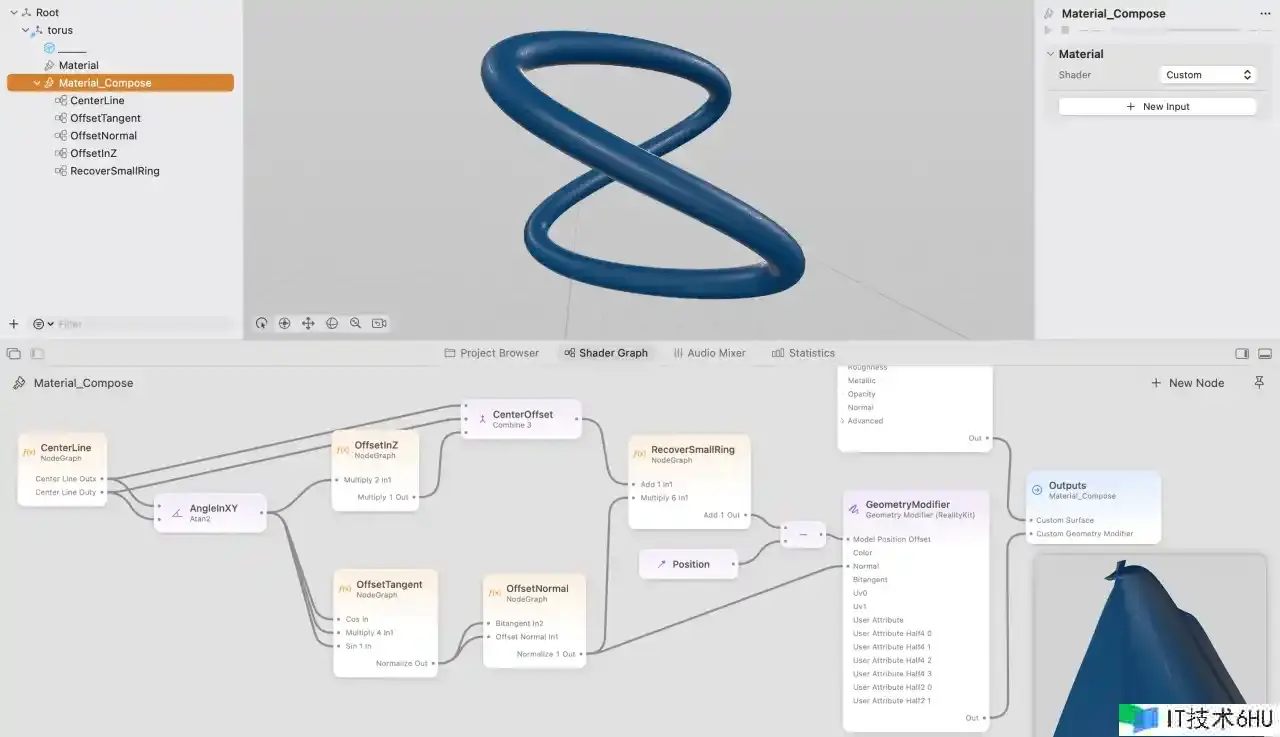
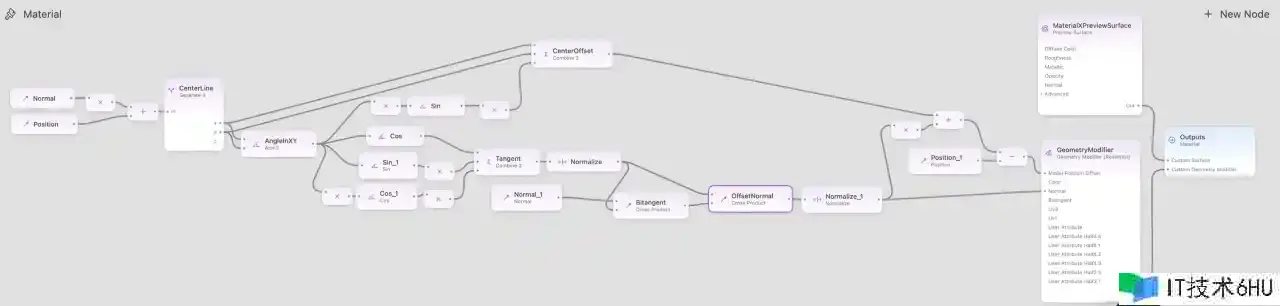
6.其他

最终，咱们选中物体，将其绕 X 轴旋转 90 度，这样看上去更像 Meta Logo 了。由于咱们的 Shader Graph 是作用在 Geometry 上，也便是模型空间坐标系，所以外部旋转并不会影响 Shader 的坐标系。

相信大家也发现了，当咱们选中物体时，显现的高亮概括仍然是原来的圆环的形状，这是由于 Shader 代码作业在 GPU 上，咱们只更改了物体的显现作用。当物体与其他物体（包括鼠标，眼动等交互操作）交互时，实际是在 CPU 上处理的物理磕碰核算，这些咱们并没有专门处理。

最终的最终，假如想要显现更多周期的动摇，只需求将下图中赤色框中倍数进行更改即可，比方改为 3个周期：

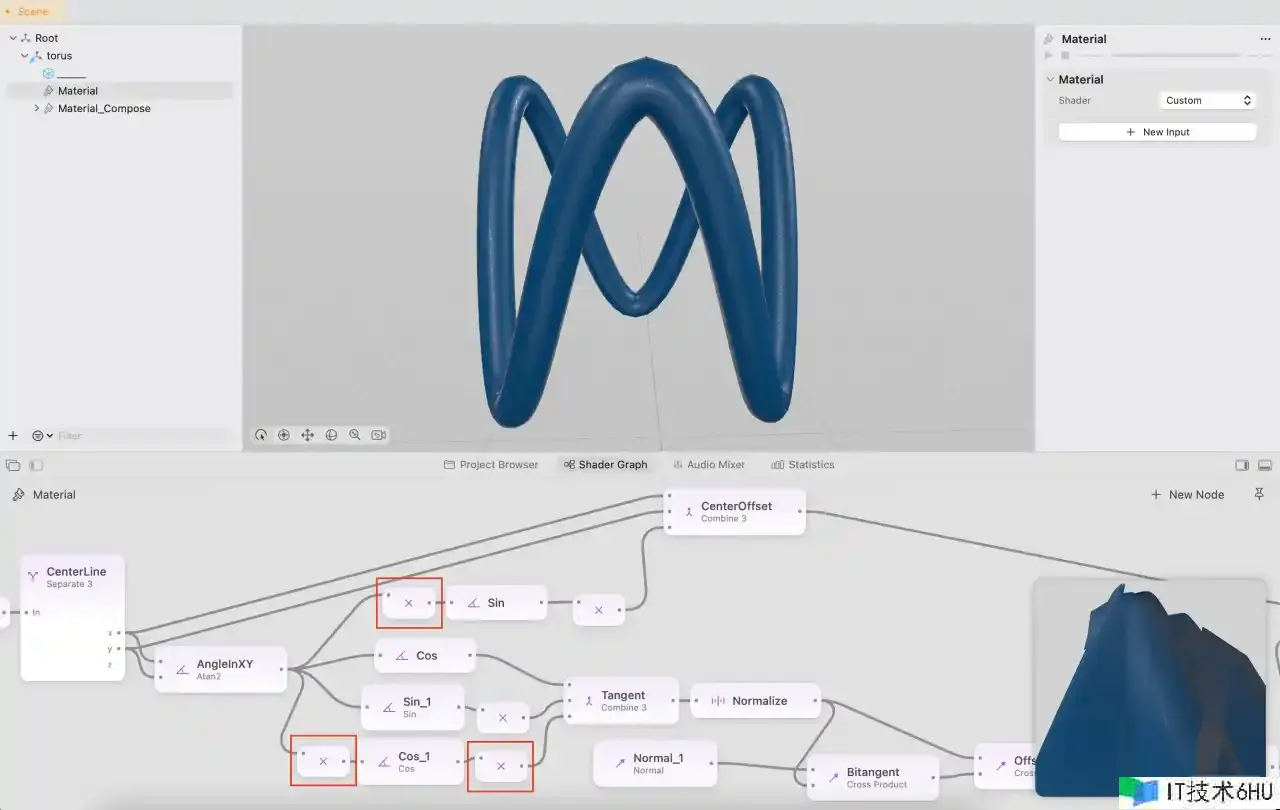
总结

此次 Reality Composer Pro 的更新十分强大，尤其是对 Shader Graph 的支撑让人惊喜，从使用者的视点，使用 Shader Graph 比直接编写 Shader 代码要容易很多，能够有用降低入门门槛。缺点方面：偶然会遇到一些类型的 bug；别的短少 Debug 功能让人编写代码时难以调试。

总之，功能强大，简练好用，引荐初学者都来试试！

本文工程代码已开源，github 地址： github.com/XanderXu/Sh…

声明：本站所有文章，如无特殊说明或标注，均为本站原创发布。任何个人或组织，在未征得本站同意时，禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益，可联系我们进行处理。