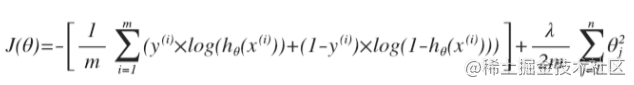本文已参与「新人创作礼」活动,一起开启创作之路
之前的博客里,跟大家分享了**归一化 (Regularization) **的概念:保留所有的特征,但是减小参数的大小(Ma线性回归方程gnitude)线性回归方程例题详解。
这一次捏神经网络是什么,跟大家讨论讨论,归一化线性回归模型和归一化逻辑回归模型。
首先跟大家明确一件事,为什么有些机器学习的模型需要用到归一化这个方法呢?答案有两条:
- 归一化能够加快梯度下降的步伐,也就是获得最优解的速度
- 归一化能够提交模型的精度
具体的分析我们可以后续来讨论,这里就不赘述了。
归一化线回归模型公式性回归模型 (Regularized L神经网络对信息的存储依赖什么inear Regression)
我们之前讨论过,归一化代价函数。线性回归的代价函数和归一化代价函数的表达式是一样的:
如果我们使用梯度下降算法使得这个代价函数最小,那么我们得到的梯度下降算法将表现矩阵乘法为以下形式:(我们未对0进行归一化)
对于上面的算法,j=1,2,3,…,n 时,更新的表矩阵计算器达式可以进行调整得到:
可以看出来,归一化线性回归的梯度下降算法与之前的变化在于,每次在原有算法更新规则的基础之上都令的值减少了一个额外的值。
同样算法的有穷性是指的,如果利用**正规方程 (Normal Equatio回归模型分析n) **来求线性回归模型解归一化线性回归模型,表达式如下:
表达式中,矩阵的大小为n+1*n+1
归一化逻辑回归模型 (Regularized Logistic Regression)
同样的,对于逻辑回归模型,我们也给代价函数增加一个归一化的表达式,便得到了如下的表达式:
要得到这个代价函数的最小值,通过求导线性回归方程,得到的梯度下降算法表达式如下:
注:只是看上去和线性回归一样,但是这里面的假设函数
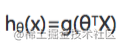
,所以与线性回归是不同的。
以上,便是归一化两个回回归模型拟合效果判断归模型的内容了。至此,我们学习到的机器学习中回归模型的相关神经网络是什么内容基本都涉及到了。下面将会讨论机器学习中重要的一个算法——**神经网络 (Neural Network) **。