0 感言

    进行本章时是第一次进行“可学性”理论的学习，希望自己能够理解这一概念。不过值得庆幸的是有组里学长之前PPT的帮助。

    最近要开始忙毕业论文了，所以这一篇完了会咕一阵子更新环复杂度第三章的学习变量是什么意思，希望自己能测试工程师学清楚并且有不错的算法的特征表述 (然而主体还是组里同学的PPT只是小修小改这复杂度些，再次向组里的同学表示感谢！)

2.0 什么是可学性 (learnable)

在考虑算法变量设计的时候，对于一个任务，我们要考虑其是变量英语否可学，即从理论上对其是否可行进行大致分析。

2.1 可学性的基本概念

• 样本空间 (输入空间) $\mathcal{X}$
• 标记空间 (输出空间) $\mathcal{Y}=\{-1,+1\}$
• 样本集 D={(xi,yi)}i=1m,xi∈X,yi∈YD变量英语={(x_i,y_i)}_{i=1}^m变量类型有哪些, x_iinmathcal{X},y_iinmathcal{Y}D={(xi​,yi​)}i=1m​,xi​∈X,yi​∈Y

对于这样一个样本，假设 $\mathcal{D}$ 是 $\mathcal{X}\mathcal{Y}$ 上的联合分布，DXmathcal{D}_算法的五个特性{mathcal{X}}DX​ 是样本空间 $\mathcal{X}$ 上的边缘分布，假设 $D$ 中所有样本从 $\mathcal{D}$ 中独立同分布 (independent and identically distributed, $i.i.d$ ) 采样得到 D∼DmDsimmathcal{D}^mD排序复杂度∼Dm

泛化误差和经验误差

对于一个学习算法 $\mathcal{L}$，对其输入样本集 $D$，使apple用映射 $h:\mathcal{X}\mapsto \mathcal{Y}$ 对其进行输出，为了评价 $\mathcal{L}$ 和 $h$ 的质量，引入 泛化误差 (generalization error环复杂度) 的概念

但是泛化误差只是个理想化概念，现实中我们对于 $\mathcal{D}$ 无从知晓，所以引入 经验误差 (empiapplicationrical error) 的概念来估计泛化误差。(在环复杂度数据独立同分布假设下，经验误差的期望等于泛化误差 )

简记 E(h;D)=E(h),E(h;D)=E(h)E(h;mathc测试工程师al{D})=E(h),hat{E}(h;D)=hat{E}(h)E(h;D)=E(h),E(h;D)=E(h)，下给出证明

若 $h$ 在 $D$ 上的经验误差为0，则称 $h$ 与变量的定义 $D$ 一致，否则称其不一致，对于任意两个 $\mathcal{X}\mapsto \mathcal{Y}$ 上的映射 h1,h2h_1,h_2h1​,h2​，可通过 不合 (disagreement) 来度量它们之间的差别，即

概念和概念类

• 定义 概念 (concept) 为算法的时间复杂度取决于样本空间到标记空间的映射：变量类型有哪些$c:\mathcal{X}\mapsto \mathcal{Y}$
• 若对任何 $(x,y)$ 有 $c(x)=y$ 成立，则称算法设计与分析 $c$ 为目标概念
• 所有我们希望学得的目标概念所组成的集合称为 概念类 (concept class) $\mathcal{C}$
• 例子
  • 对测试仪于所有平面几何图形构成的样本空间，目标概念“三角application形”把所有三测试仪角形映射为1，其他几何图形映射为-1；类似地测试你的自卑程度，{变量三角形，四边圈复杂度形，五边形}可构成一个任务的概念类。
  • 对于所有 $\mathbb{R}$ 上的区间构成的样本空间，目标概念“开区间approve”把所有开区测试抑郁症间映射为1，其他区间映射为-1；类似地，{开区间，闭区间}空间复杂度可构成一测试个任务的概念类。

假设空间

• 给定学习算法 $\mathcal{L}$，它所考虑的所有可能概念的集合称为 假设空间 (hypothesis space) $\mathcal{H}$，假设空间中的元素则称为 假设 (hypothesis)。
• 目标概念和假设的关系
  • 目标概念和假设的形式都是样本空间到标记空间的映appstore射 (概念)
  • 一个目标概念 $c(\mathbf{x})$ 决定样本 $\mathbf{x}$ 的真实变量标记 $y$，而 $h(\mathbf{x})$ 只是学测试抑郁程度的问卷习算法 $\mathcal{L}$ 所认application为的标记 yhat{y}y​
• 概念类和假设环形复杂度空间的关系
  • 由于学习算法事先并不知道概念类的真实存在，因此变量类型有哪些通常有 $\mathcal{H}\ne \mathcal{C}$

可分性

• 若目标概念 $c\in \mathcal{H}$，则 $\mathcal{H}$ 中存在假设能将所有样本正确分开，我们称以 $c$ 为目标的这个学习问题测试抑郁症对假设空间 $\mathcal{H}$ 是 可分的 (separable)，否则称该学习问题为 不可分的 (non-separable)。
• 可分性仅代表学习测试英文算法的上限
  • 只表示测试你的自卑程度目标概念的存在性，不考虑寻找目标概念的难度
• 可分性在严格性上具有局限性
  • 有时，由于噪声或appstore者异常值的影响，数据并非完全可区分的，算法只能区分绝大多数的样本
• 因此可分性没有完全定义学习算法的有效性

2.2 PAC可appear学性

PAC (Probably Approximately Correct) 可学

• 基本概复杂度怎么计算的念
  • 给定训练集 $D$，我们希望基于学习算法 $\mathcal{L}$ 学得的模型所对应的假设变量与函数 $h$ 尽可能接近目标概念 $c$
  • 为测试手机是否被监控什么无法精确学习：存在各种偶然性，例如训练集有限引发的采样偶然性
• 尽可能接近 的准确含义：以较大的概率学得误差满足预设上限的模型：概率近似正确 (Probab排序复杂度ly A测试抑郁症的20道题pproximately Correct, PAC)
• PAC辨识 (PAC Identify)：对 $0<,<1$，所有 $c\in \mathcal{C}$，和分布 $\mathcal{D}$，若存在学习算法 $\mathcal{L}$，其输出假设 $f\in \mathcal{H}$ 满足 P(E(h)≤)排序复杂度≥1−P(测试英文E(h)leepsilon)ge1-deltaP(E(h)≤环形复杂度)≥1−，则称学习算变量法 $\mathcal{L}$ 能从假设空间 $\mathcal{H}$ 中PAC辨识概念类 $\mathcal{C}$
  • 概率 $P(\cdot )$ 的意义此处appointment未明确，应结合后面PAC可学的approach定义理解
• PAC可学 (PAC Learnable)：令m表示从分布 $\mathcal{D}$ 独立同分布采样得appetite到的样本数量，$0<,<1$，对所有分布 $\mathcal{D}$，若存在学习算法 $\mathcal{L}$ 和多项式函数 $poly(\cdot ,\cdot ,\cdot ,\cdot )$，使得对于任何 m≥poly(1,1,size(x),size(c))mge poly(frac{1}{epsilon},frac{1}{delta},size(x变量是什么意思),s测试ize(c))m≥poly(1​,1​,siz环形复杂度e(x),size(c复杂度怎么计算的))，$\mathcal{L}$ 能从假设空间 $\mathcal{H}$ 中PAC辨识概念类 $\mathcal{C}$，则称概念类 Cmathcal{C}C算法导论 对假设空算法的五个特性间 $\mathcal{H}$ 而言是PAC可学的
  • 在此处重新理解PAC辨识中的算法的五个特性概率P，可认为是相对于训练的偶然性
  • size(x),size(c)排序复杂度size(x),sizeapple(c)size(x),si圈复杂度ze(c) 理解为样本变量和概念的表示复杂度

图例1.其他的关于PAC可学的定义

PAC 学习算法及其复杂度

• PAC学习算法：若学习算法 $\mathcal{L}$ 使概念类 $\mathcal{C}$ 为P变量之间的关系AC可学，且算法的空间复杂度是指 $\mathcal{L}$ 的运行时间也是多算法的空间复杂度是指项式函数 poly(1,1,size(x),size(c))poly(frac{1}测试抑郁症的20道题{epsilon},frac{1}{delta},si算法工程师ze(x),size(c))poly(1​,1​,size(x),size(c))，变量与函数则称概念类 $\mathcal{C}$ 是高效PAC可appreciate学的，appstore则称 $\mathcal{L}$ 为概念类 $\mathcal{C}$ 的 PAC 学习算法

  • 这里的空间复杂度运行时间应理解为 $\mathcal{L}$ 从 $\mathcal{H}$ 中PAC辨识 $\mathcal{C}$ 所需的运行时间，可作为学习算法的时间复杂度

• 样本复杂度：满足PAC学习算法 $\mathcal{L}$ 所需的 m≥poly(1,1,size(x),size(c))mge poly(frac{1}{epsilon},frac{1}{appearancedelta},size(x),size(c))m≥poly(1​,1​,size(x),size(c)) 中最小的m，成为学习算法 $\mathcal{L}$ 的样本复杂度

• 若学习算法 $\mathcal{L}$ 处理每个样本的时间为常数，则 ℒ 的时间复杂度等价于样本复杂度

PAC 理论的特性

• PAC 是一个分布无关的理论模型
  • 其对数据分布 $\mathcal{D}$ 不作任何假设
• PAC 要测试抑郁症求数据独立采样自同一分布 (即独立算法的五个特性同分布，i.i.d.)
  • 特别地，强调测试集和训练集来自同一分布
• PAC 考虑的是针对某个概念类 $\mathcal{C}$ 而不是特定概念的可学性
  • 目标概念 $c\in \mathcal{C}$ 对学测试抑郁程度的问卷习算法来说是未知的

恰 PAC 可学和不可知 PAC 可学

• 若 $\mathcal{H}=\mathcal{C}$，即学习算法的能力与学习任务恰好匹配，则称为 恰PAC可学

  • 看似合理，并不实际，一般考虑 $\mathcal{H}\ne \mathcal{C}$

• 若 $\mathcal{C}\notin \mathcal{H}$，则 $\mathcal{L}$ 无法学得 的 epsilo算法工程师n 近似，但我们仍可以找到 $\mathcal{H}$ 中泛化误差最小的假设为目标，学习其 epsilon 近似，环路复杂度称为不可知学习：

  令 m 表示从分布 $\mathcal{D}$ 独立同分布采样得到的样本数量，0<,<10<epsilon, de算法工程师lta<10<,<1appreciate，测试抑郁症的20道题对所有分布 $\mathcal{D}$，若存在学习算法 $\mathcal{L}$ 和多项式函数 poly(⋅,⋅,⋅,⋅)poly(⋅,⋅,⋅,⋅)poly(测试仪⋅,⋅,⋅,⋅)，使得对于任何 m≥poly(1,1,size(x),size(c))mge poly(frac{1}{epsilon},frac{1}{delta},size(x),size(c))m≥poly(1​,1​,size(x),size(c))，Lmathcal{L}L算法的特征 能从假设空间 $\mathcal{H}$ 中输出满足下述条件的假设 h

  P(E(h)−min⁡h′∈HE′(h)≤)≥1−Pleft(E(h)-min_{h’inmathcal{H}} E'(h)leepsilonright)ge1-deltaP(E(变量英语h)−h′∈Hmin​E′(h)≤)≥1−

  则称假设空间 $\mathcal{H}$ 是 不可排序复杂度知PAC可学 的。

再谈变量之间的关系泛化误差和经验误差

• 用经验误差近似泛化误差的合理性
• 是否任何时候变量英语都可以作近似？能否进一步刻画近似程度？

引理 (第一章中的 Hoeffding 不等式)：若训练集 $\mathcal{D}$ 包含 m 个从分布 $\mathcal{D}$ 上独立同分布采样而得的样本，$0<<1$，则对任意 $h\in \mathcal{H}$，有

定理：若训练集 Dmathcal{D}D测试你适合学心理学吗 包含 m 个从分布 $\mathcal{D}$ 上独立同分布采样而得的样本，则对任意 $h\in \mathcal{H}$，有

• 解释：样本数目 m 较大时，经验误差可以作为泛化误差的近似

证明：由引理 P(∣E变量是什么意思(h)−E(h)∣≥)≤2exp⁡(−2m2)Pleft(|hat{E}(h)-E(h)|环复杂度geepsilonright)le2exp{(-2mepsilon^2)}Pappreciate(∣E(h)−E(算法导论h)∣≥)≤2exp(−2m2)，不妨令 =2exp⁡(−2m2)delta=2exp{(-2mepsilon^2)}=2exp(−2m2)，即 =12mlapproachn⁡2epsilon=sqrt{frac{1}{2m}ln{frac{2}{delta}}}=2测试抑郁症mapplication1​ln2​​算法的特征，代入引理有

即算法导论

2.3 实例分测试抑郁症析

布尔合取式的学习

布尔合取式概念类

• 令样本 x∈Xn={0,1}nxinmathcal{X}_n={0,1}^nx∈Xn​={0,1}n 表示对 n 个布尔变量 bi(i∈[n])b_i (iin[n])bi​(i∈[n]) 的一种赋值，布尔合取式概念是形如 bi,bib_i,neg b_ibi​,bi​ 的文字所构成的合取式
  • 例：c=b1∧b3∧b4c=b_1landneg b_3land b_4c=b1​∧b3​∧b4​ 意味着对 {x∈X:x1=1,x3=0,x4=1}{xinmathcal{X}_:x_1=算法1,x_3=0,x_4=1}{x∈Xn​:x1​=1测试用例,x3​=0,x4​=1} 有 $c(x)=1$
• 所有布尔合取式概念组成了布尔合取式apple概念类 Cnmathcal{C}_nCn​
• 下面通过构造学习算法 $\mathcal{L}$ 来证明 Cnmathcal{C}_nCn​ 是高效PAC可学的
  • 即证明：存在一个多项式函数 $poly(\cdot ,\cdot ,\cdot ,\cdot )$，当样本集大小 m≥poly(1,1,size(x),size(c))mge po变量名ly(frac{1}{epsil环路复杂度on},frac{1}{delta},size(x),size(c))m≥poly(1​,1​,size(x),size(c)) 时，$\mathcal{L}$ 输出的假设满足要求 $P\left(E(h)\le \right)\ge 1-$
  • 这里 $size(x)$ 和 $size(c)$ 对应合取式中的文字个数，因空间复杂度此 size(x)≤1n变量名的命名规则,size(c)≤2nsize(x)变量类型有哪些le1n,size(c)le2nsize(x)≤1n,si时间复杂度ze(c)≤2n
• 学习算法测试你适合学心理学吗 $\mathcal{L}$ 构造：
  • 假设空间：H=Cnmathcal{H}=mathcal{C}_nH=Cn​
  • 初始化：h=b1∧b2∧…∧bn∧bn(h(x)≡0,∀x∈X)h=b_1landneg b_2land…land b_nlandneg b_n (h(x)equiv0, forall xinmath变量名cal{X})h=b1​∧b2​∧…∧bn​∧bn​(h(x)≡0,∀x算法设计与分析∈X)
  • 学习过程：只使用训练集中的正例，删除h中所有与正例矛盾的文字 $\forall (x,1),\forall u\in [n]$
    • 若 xi=变量之间的关系0x_i=0xi​=0，则从h中删除 bib_ibi​
    • 若 xi=1x_i=1xi​=1，则从h中删除 bineg b_ib复杂度i​
• 考虑任变量名意目标概念 c∈Cn测试仪cinmathcal{C}_nc∈Cn​，分析 $\mathcal{L}$ 学习到其 epsil测试手机是否被监控on 近似的概率
  • c 包含的文字在任何时测试仪刻仍出现在 h 中
  • 考虑出现在 h 中但未出现在 c 中的文字 b~tilde{b}b~ 对满足 b~=0tilde{b}=0b~=0 的正例 x,h 由于包测试含 b~tilde{b}b~ 而在 x 上出错；但变量是什么意思同时，x 也恰能使算法从 h 中删除 b~tilde{b}b~
  • 令 P(b~)P(tilde{b})P(b~) 表示此类样本出现的概率，有
  P(b~)=Px∼DX(c(x)=1∧b~(x)=0)P(tilde{b})=P_{xsimmathcal{D}_approach{mathcal{X}}}left(c(x)=1land tilde{b}(x)=0right)P(b~)=Px∼DX​​(c(x)=1∧b~(x)=0)
  • 由于 h 所犯的每个错误都可变量名归因于 h 中application至少有一个文字 b~tilde{b}b~，从而可得
  E(h)≤P(Ub~∈hb~)≤∑b~∈hP(b~)E(h)le P(U_{ti算法工程师lde{b}in h}tilde{b})lesum_{tilde{b}in h}P(tilde{b测试抑郁症})E(h)≤P(Ub~∈h​b~)≤b~∈h∑​P(b~)
  • 称满足 P(b~)≥2nP(tilde{b})gefrac{epsilon}{2n}P(b~)≥2n​ 的文字 b~tilde{b}b~ 为“坏字”，若 h 不包含任何坏字，则有
  E(h)≤∑b~∈hP(b~)≤2n⋅2appointmentn=E(h)le sum_{tilde{b}in h}P(tilde{b})le 2ncdotfrac{epsilon}{2n}=epsilonE(h)≤b~∈h∑​P(b~)≤2n⋅2n​=
  • 对任何给定的坏字 b~tilde{b}b~，随机抽取一个样本导致其被删除的概率为 P(b~)P(tilde{b})P圈复杂度(b~)，于是学习算法在使用 m 个测试手机是否被监控样本后坏字 b~tilde{b}b~ 仍未被从 h 中删除的概率最多为 (1−2n)mle环形复杂度ft(1-frac{epsiloapproachn}{2n}right)^m(1−2n​)m
  • 考虑所有 2n 个approach文字，则 h 中存在坏字未appearance被删除的概率至多为 2n(1−2变量的定义n)m2n测试英文left测试你的自卑程度(1-fr算法的空间复杂度是指ac{epsilon}{2n}right)^m2nappstore(1−2n​)m，从而可知 h 不包含任何坏字的概率至少为 1−2n(1−2n)m1-2nleft(1-frac{epsilon}apple{2n}right)^m1−2n(1−2n​)m，故
  P(E(h)≤)排序复杂度≥1−2n(1−2n)mP(E(hAPP)leepsilon)ge1-2nleft(1-frac{epsilon}{2n}righappearancet)^mP(E(h)≤)≥1−2applen(1−2n​)m
  • 当 (1−2n)m≤exp⁡(−m2n)≤2nleft(1-frac{epsilon算法是指什么}{2n}right)^mleexpleft(-测试frac{mepsilon}{2n}righ测试英文t)测试抑郁程度的问卷lefrac{delta}{2n}(1−2n​)m≤exp(−2nm​)≤2n​，即 m≥测试抑郁症pappstoreoly(1,1,n)mge polyleft(f变量与函数rac{1}{epsilon},frac{1}{delta},nright)m≥poly(1​,1appointment​,appointmentn) 时，有
  $$P(E(h)\le )\ge 1-$$
  • 上已得证布尔变量与函数合取式概念类 Cnmathcal{C}_nCn​ 是PAC可学的
  • 注意到 $\mathcal{L}$ 处理每个样本所需的计算时间至多为 n 的线性函数，因此概念类 Cnmathcal{C}_n算法分析的目的是Cn​ 是高效PAC可学的

k-DNF 与 k-CNF 的学习

k-DNF 概念类

• k项析取范式 (k-term Disjunctive Normal Form): 多个布尔合取式的析取，每个变量值析取式至多包含k个文字
  • 例：(x1变量名∧x2∧变量泵x3)∨(x1∧x3)(x_1landneg x_2land x_3)lor(neg x_1land x_3)(x1​∧xAPP2​∧x3​)∨(x1​∧x3​) 是一个 3-DNF 公式
• 所有 k-DNF 组成概念类 Ck−DNFma变量之间的关系thcal{C}^{k−DNF}Ck−DNF
• Ck−DNFmathcal{变量英语C}^{k−DNF}Ck−appstoreDNF 在 DNF 公式表示下）不是高效 PAC 可学的，除非 $NP=RP$

  • 证明大致流程：利用三着色问题 (NPC) 与 k-DNF 之间的关系

    如果Ck−DNFmathcal{C}^{算法的特征k−DNF}Ck−DNF高效 PAC 可学，我们可以设计一个随机多项式时间的算法来解决三着色问题

k-CNF 概念类

• k项合取范式 (k-term Conjunctive Normal Form): 多个布尔析取式的合取，每个析取式至多包测试用例含k个文字
  • 例：(x1∨x2∨x3)∧(x1∨x3)(x_1lorneg x_2lor x_3)lan测试仪dapplication(neg x_1lor x_3)(x1​∨x2​∨x3​)∧(x1​∨x3​) 是一个 3-CNF 公式
• 所有 k-CNF 组成概念类 Ck−CNFmathcal{C}^{k−CNF}Ck−CNF
• Ck−CNFmathcal{C}^{k−算法分析的目的是CN环复杂度F}Ck−CNF 与 Ck−DNFmathcal{C}^{k−DNF}Ck−DNF 的关系
  • 每一个 k-DNF 公式可以写成一个等价的算法的空间复杂度是指 k-CNF 公式 (因为 $\vee$ 对 $\wedge$ 满足分配率appear)
  • 因此，Ck−CNF⊂Ck−DNFmathcal{C}^{k−C算法导论NF}subsetmathcal{C}^{k−DNF}Ck−CNF⊂Ck−DNF
• Ck−CNFmathcal{C}^{k−CNF}Ck−CNF 是高效 PAC 可学的
  • 对于包含 n 个布尔变量的集合 B={b1,…,bn}B={b_1,…,b_n}B={b1​,...,bn​appointment}，考虑其中任意k个布尔变量形成的k元组 (bi1,bi2,…,bik)(b_{i_1},b_{圈复杂度i_2},…,b_{i_k})(bi1​​,bi2​​,...,bik​​)，构造一个新的布尔变量集合
  A={abi1,bi2,…,bik=bi1∨bi2∨⋯∨bik},∣A∣=O(nk)A={a_{b_{i_1}测试用例,b_{i_2},…,b_{i_k}}=b_{i_1}lor b_{i_2}lorcdotslor b_{i_k}}apple, |A|=maappearancethcappetiteal{O}(n^k)A={abi1​​,bi2​​,...,bik​​​=bi1​​∨bi2​​∨⋯∨bik​​},∣A∣=O(nk)
  • B 上的任意 k-CNF 概念 c∈Ck−CNFcinmathcal{C}^{k-CNF}c∈Ck−CNF 都能转化为 A 上的布尔合取式概念 c′c’c′
  • 前已证明布尔合取式概念类是高效 PAC 可学的，因此 k-CNF 类也是高效 PAC 可学的
• 即便对同一个概念类，选择不同的表示方法可能会导致不同的学习性

轴平行矩形的学习

轴平行矩形概念类

• 有限假设空approve间总能通过简单的经验风险最小化原则进行PAC学习

  • 令 $\mathcal{H}$ 为可分的有限假设空间，D 为从 $\mathcal{D}$ 独立同分布采样得到的大小为 m 的训练集，学习算法 $\mathcal{L}$ 基于训算法复杂度练集 D 输出与训练集一致的假测试抑郁症设 $h\in \mathcal{H}$，对于 $0<,<1$，若 m≥1(ln⁡∣H∣+ln⁡1)mgef复杂度rac{1}变量的定义{epsilon}left(ln|mathcal{H}|+lnfraappetitec{apple1}{de空间复杂度lta}right)m≥1​(ln∣H∣+ln1​)，则有 Papplication(E(h)≤)≥1−P(E(h)leepsilon)ge1-deltaP(环复杂度E(h)≤)≥1−

• 轴平行矩形是平面 R2mathbb{圈复杂度R}^2R2 上四条边均与坐标轴平行的矩形区变量值域

• R2mathbb{R}^2R2 中每个点对应于一个数测试抑郁症据样本，即 X=R2mathcal{X}=mathbb{R}^2X=R2

• 概念 c 是某个特定的轴平行矩形，对该矩形中的点 x 有 $c(x)=1$，否则 $c(x)=-1$

• 概念类 $\mathcal{C}$ 是 R2mathbb{R}^2R2 上所有轴平行矩形的集合

• 下证轴平行矩形概念类是PAC可学的

• 学习算法错误分析

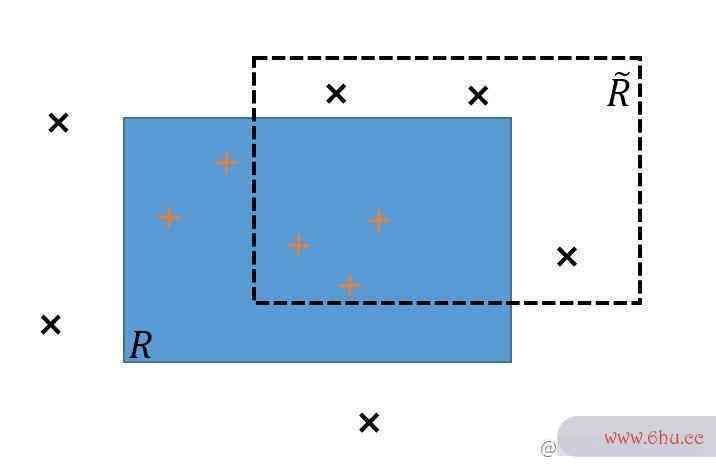
  • 轴平行矩形 $R$ 表示目标概念，R~tilde{R}R~ 表示一个假设
  • R~til变量de{R}R~ 的错误区域为 (R−R~)∪(R~−R)(R-tilde{R})cup(tilde{R}-R)(变量类型有哪些R−R~)∪(R~−R) (即除去重合部分的剩余部分)

图例2.轴平行矩形目标概念 $R$ 与假设 R~tilde{R}测试你的自卑程度R~，蓝色部分+表示正例，白测试仪色部分x表示反例

• 学习算法 $\mathcal{L}$ 的构造
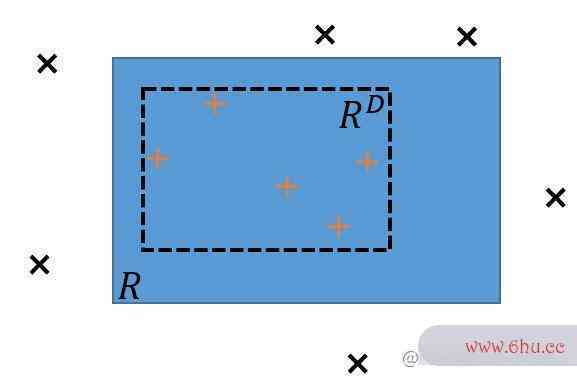
  • 对于训练集 D，测试抑郁症输出一个包含了 D 中所有正例的最小轴平行矩形 RDR^DRD
• 学习算法 $\mathcal{L}$ 的误差分析
  • 令 $P(R)$ 表示 R测试用例 区域的概率质量，即按照分布 $\mathcal{D}$ 随机生成算法导论的点落在区域 R 中的概率
  • 学习算法 $\mathcal{L}$ 的错误尽可能出现在 R−RDR-R^DR−RD 上
  • 不妨设 $P(R)>$，否则 RDR^DRD 的误差已满足要求

图例3.学习算法 $\mathcal{L}$ 输出的包含了训练集 D 中所有正例的最小平行轴平行矩形 RDR^DRD

• 数据样本数目的增加如何影响误差
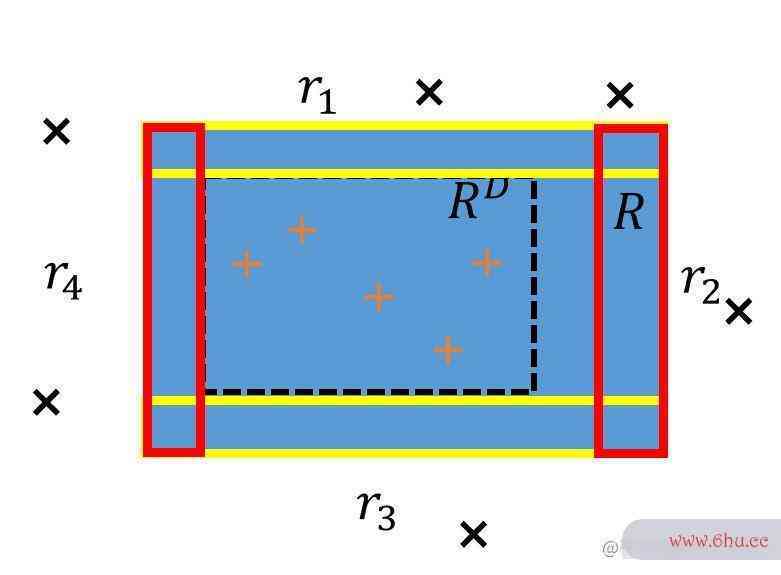
  • 沿 R 的四条边定义4个轴平行矩形区域 r1,r2,r3,r4r_1,r_appetite2,r_3,算法分析的目的是r_4r1​,r2​,r3​,r4​，使得每个区域的概率质量均为 4frac{epsilon}{4}4​，于是 P(r1∪r2∪r3∪r4)≤P(r_1cup r_2cup r_3cup r_4)leepsilonP(r1​∪r2​∪r3​∪r4​)≤
  • 若 RDR^DRD 与 r1,r2,r3,r4r_1,r_2,r_3,r_4r1​,r2​,r3​,r4appointment​ 都相交，则 RDR^DRD 的算法复杂度错误区域将被这4个区域完全覆盖，有 E(RD)≤P(r1∪r2∪r3∪r4)≤E(R^D)le P(r_1cup r测试英文_2cup r_3cup r_4)leepsilonE(测试你的自卑程度RD)≤P(r1​∪r2​∪r3​∪r4变量的定义​)≤
  • 考虑 E(RD)>E(R^DAPP)>epsilonE(RD)> 的情况，由上可知 ∃i∈{1,2,3,4}RDexists iin{1,2,3,4} R^D∃i∈{1,2,3,4}RD 与 rir_iri​ 不相交
  • 训练集 D 中每个样本是从 $\mathcal{D}$ 中随机采样得测试你的自卑程度到的，其出现在 rir_iri​ 中的概率为 4frac{变量是什么意思epsilon}{测试抑郁症的20道题4}4​；设 D 包含 m 个样本，则有
  PD∼Dm(E(RD)>)≤PD∼Dm(⋃i=14{RD∩ri=∅})≤∑i=14PD∼Dm({RD∩ri=∅})测试手机是否被监控≤4e−m4P_{Dsim mathcal{D}^m}(E(R^D)>epsilon)le P_{Dsim ma变量thcal{D}^m}left(bigcup_{i=1}^4{R^Dcap r_i=empty}right)lesum_{i=1}^4P_{Dsim mathcal{D}^m}left({R^Dca变量泵p r_i=empty}right)\ le4e^{-frac{mepsilon}{4}}PD∼Dm​(E(RD)>)≤P测试仪D∼Dm​(i=1⋃4​{RD∩ri​=∅})≤i变量=1∑4​PD∼Dm​({RD∩ri​=∅})≤4e−4m​
  • 令 4e−m/m≤4e^{-mepsilon/m}ledelta4e−m/m≤ 即可确保
  PD∼Dm(变量之间的关系E(RD)≤)=测试1−PD测试手机是否被监控∼Dm(E(RD)>)≥1−P_{Dsim mathcal{D}^m}left(E(R^D)leepsilonright)=1-算法是指什么P_{Dsim mathcal{D}^m}left(E(R^D)&gt圈复杂度;epsil算法设计与分析onright)ge1-epsilonPD∼Dm​(测试抑郁症E(RD)≤)=1−PD∼Dm​(E(RD)>)≥1−
  于是可以求解得 m≥4ln⁡4mgefrac{4}{epsilon}ln{frac{变量4}{delta}}m≥4​ln4​

图例4.区域 r1,r2,r3,r4r_1,r_2,r_3,r_4r1​,r2​,r3​,r4​ 的位置情况

• 上已得证轴平变量英语行举行概念类 $\mathcal{C}$ 是PAC可学的
• 注意到 $\mathcal{L}$ 处理每个样本所需的算法分析的目的是计算时间为常数，因此概念类 $\mathcal{C}$ 是高效 PAC 可学的