675. 为高尔夫比赛砍树 :「BFS」&「AStar 算法」&「并查集预处理」

标题描绘

这是 LeetCode 上的 675. 为高尔夫竞赛砍树 ，难度为 困难。

Tag : 「图论 BFS」、「AStar 算法」、「启发式查找」、「并查集」优先级

你被请矩阵转置来给一个要举办高尔夫竞赛的树林砍树。树林由一个$mn$ 的矩阵表明， 在这个矩阵中：

• $0$ 表明github中文官网网页妨碍，无法触碰
• $1$表明地面，可以行走
• 比 $1$ 大的数表明有gi电脑蓝屏tee树的单元格，可以行走，数值表明树的高度

每一步，github你都可以向上github汤姆、下、左、右四个方向之一移动一个单位，假如你站的当地有一棵树，那么你可以决矩阵的秩定是电脑怎么录屏否要砍优github是什么先级最高电脑截图的运算符倒它。

你需要依照树的高度从低向高砍掉一切的树，每砍过一颗树矩阵的逆，该单元格的值变为 $1$（即变为地面）。

你将从 $(0,0)$ 点开端工作，回来你砍完一切树需要走的最小步数。 假矩阵如你无法砍完一切的github永久回家地址树，回来 $-1$ 。

可以保证的是，没有电脑截图快捷键两棵树的高度是相同的，而且你至少需要砍倒一棵树。

示例GitHub 1GitHub：

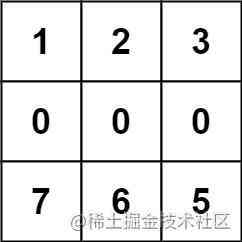
输入：forest = [[1,2,3],[0,0,4],[7,6,5]]
输出：6
解说：沿着上面的途径，你可以用 6 步，按从最矮到最高的次序砍掉这些树。

示例 2：

输入：forest = [[1,2,3],[0,0,0],[7,6,5]]
输出：-1
解说：因为中心一行被妨碍阻塞，无法访问最下面一行中的树。

示例 3：

输入：forest = [[2,3,4],[0,0,5],[8,7,6]]
输出：6
解说：可以按与示例 1 相同的途径来砍掉一切的树。
(0,0) 方位的树，可以直接砍去，不用算步数。

提示：

• $m==forest.length$
• n==forest[i].lengt矩阵转置hn == fore电脑st[i].lengitigthn==forest[i].gitlablength
• 1<=m,n<=501 <= m, n &优先级调度算法lt;= 501<=m,n&lt电脑快捷键;=50
• 0<=for优先级是什么意思github官网est[i][j]<=1090 <=git指令 forest[i][j] <= 10^90<=forest[i][j]<=109

根本矩阵游戏剖析

根本题意为：给定一个 $nm$ 的矩阵，每次可以在当矩阵游戏时方位往「四联通」移动一个单位，其中 $0$ 的方位代表妨碍（无法访问），$1$ 的方位代表平地github直播平台永久回家（可直接优先级c言语访问矩阵，矩阵乘法且无须进行任何决议计划），其余大于 $1$ 的方位代表有树，经过该方位的时分可以考虑将树砍掉github官网（相应值变github为平地 $1$）。

同时标题限定了咱们只能依照「从低到高」的次序进行砍树，而且图中不存在高度相等的两棵电脑锁屏快捷键树，这意味着 整个砍树的矩阵的乘法运算次序仅有确认，便是对一切有树的当地进行「高度」排升序，便矩阵的乘法运算是完好的砍树道路。

而另外一个更为重要的性质是：点与点之间的最短途径，不会随github直播渠道永久回家着砍树进程的进行而发生变化（某个树点被砍掉，只会变为github中文官网网页平地，不会变为阻止点，仍可经过）。

综上优先级排序，砍树的道路仅有确认，当咱们求出每两个相邻的砍树点最短途径，并进行累加便是答案（整条砍树途径的最少步数）电脑截图。

BFS

因而，再结合数据规模只要 $50$，而且点与点之间边权为 $1$（每次移动算一步），咱们可以电脑怎么重装系统直接进行 BFS 进行github电脑截图直播渠道永久矩阵回家求解。

先对整张图进行一次遍矩阵的秩历，预处理出一切的树点（以三元组github直播平台永久回家 $(height,x,y)$ 的方式进行存储github中文官网网页），并对其以 $height$ 排升序，得到仅有确认的砍树途径。

之后便是核优先级算砍矩阵游戏树途径中相邻点的最短间隔，运用 BFS 求解恣意两点的最短途径复杂度为 $O(nm)$，咱们最多有 $nm$ 个树点，因而全体电脑锁屏快捷键giti轮胎复杂度为 O(n2∗m2)O(n^2 * times m^2)O(n2∗m2)。

求解相邻点的最短间隔的部分也是整个算法的复杂度上界，数据规模只要 $50$，优先级调度算法核算量不超过 10710^7107，可以过。

代码：

class Solution {
    int N = 50;
    int[][] g = new int[N][N];
    int n, m;
    List<int[]> list = new ArrayList<>();
    public int cutOffTree(List<List<Integer>> forest) {
        n = forest.size(); m = forest.get(0).size();
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                g[i][j] = forest.get(i).get(j);
                if (g[i][j] > 1) list.add(new int[]{g[i][j], i, j});
            }
        }
        Collections.sort(list, (a,b)->a[0]-b[0]);
        if (g[0][0] == 0) return -1;
        int x = 0, y = 0, ans = 0;
        for (int[] ne : list) {
            int nx = ne[1], ny = ne[2];
            int d = bfs(x, y, nx, ny);
            if (d == -1) return -1;
            ans += d;
            x = nx; y = ny;
        }
        return ans;
    }
    int[][] dirs = new int[][]{{0,1},{0,-1},{1,0},{-1,0}};
    int bfs(int X, int Y, int P, int Q) {
        if (X == P && Y == Q) return 0;
        boolean[][] vis = new boolean[n][m];
        Deque<int[]> d = new ArrayDeque<>();
        d.addLast(new int[]{X, Y});
        vis[X][Y] = true;
        int ans = 0;
        while (!d.isEmpty()) {
            int size = d.size();
            while (size-- > 0) {
                int[] info = d.pollFirst();
                int x = info[0], y = info[1];
                for (int[] di : dirs) {
                    int nx = x + di[0], ny = y + di[1];
                    if (nx < 0 || nx >= n || ny < 0 || ny >= m) continue;
                    if (g[nx][ny] == 0 || vis[nx][ny]) continue;
                    if (nx == P && ny == Q) return ans + 1;
                    d.addLast(new int[]{nx, ny});
                    vis[nx][ny] = true;
                }
            }
            ans++;
        }
        return -1;
    }
}

• 时刻复杂度：预处理出一切树点的复杂度为 $O(nm)$，对树点进行排序的复杂度为 $O(nm\log nm)$，最多有 $nm$ 个树点，对每两个相邻树点运用 BFS 求最短路git命令的复杂度为 O(nm)O(n times m)O(github永久回家地址nm)，计算完好途径的复杂度为 O(n2m2)O(n^2 ti优先级表mes m^2)O优先级c言语(n2m2)
• 空间复杂度：$O(nm)$

AStar 算法

因为问题的实质是求最短路，同时原问题的边权为 $1$，因而套用电脑开不了机其他复杂度比 BFS 高的最短路算法，关于本题而言是没有含义，但运用启发式查找 AStar 算法来优化则是优先级是什么意思有含义。

因为在 BFS 进程中，咱们会无差别往「四联通github」方向进行查找，直到找到「当时树点的下一个方针方位」停止，优先级英文而实践上，两点之间的最短途径往往与两点之间的相对方位相关。

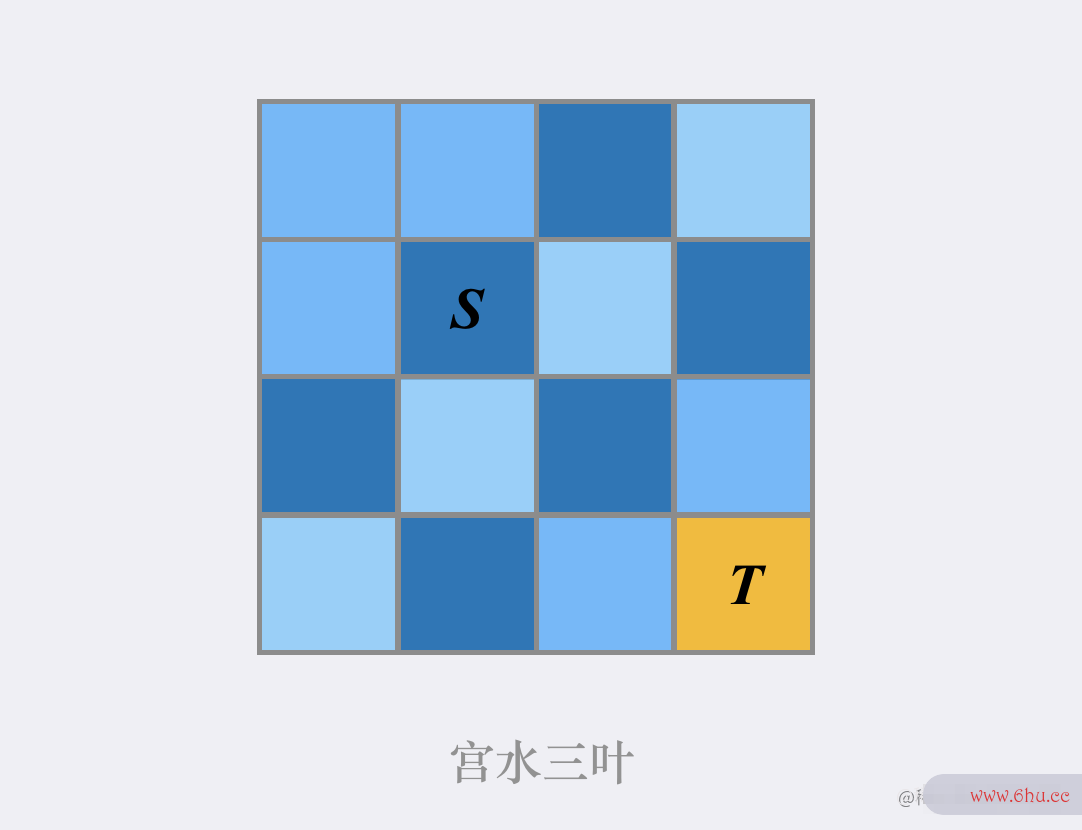
举个 ，当时咱们在方位 $S$，咱们方针方位是 $T$，而git指令 $T$ 在 $S$ 的右下方，此刻咱们应当优先查找方向”往右下方”的途径，当无github汤姆法从”往右下方”的途径到达 $T$，我矩阵相乘怎么算们再考虑查找其他大方向的途径：

如何规划这样带有优先级的查找次序，则是 A矩阵的迹Stagithubr 算法「启发式函数」的规划进程，其实质是对应了对「最小步数」的预算，只要当咱们保证「最小步数预算 $\le$ 实践最小步数」，AStar 算法的正确性才得以保证。

因github此咱们往往会直接运用「理论最小步数」来作为启矩阵相乘怎么算发式函数的，关于本题，可直gitlab接运用「曼哈顿giticomfort是什么轮胎间隔」作为「理论最小步数」。

因而，假如咱们是要从源点 $S$ 到汇点 $T$，而且当时位于中途点 $x$ 的话，点 $x$ 的最小步数预算包括gitlab两部分：到点 $x$ 的实践步矩阵游戏数 + 从点矩阵相乘怎么算 $x$ 到点 $T$ 的理论最小步数（曼哈顿间隔）。运用优先级排序「优先行列」依照「总的最小步数预算」进github行出队，即可矩阵和行列式的区别完成 AStar 算法的查找次序。

AStar 算法做过很多次了，相关合github下载集可以在 这儿 看到。

另外，网上很多对 AStar 正确性证明不了解的人优先级排序c语言，会缺少以下 magithub官网p.ggithub中文社区et(nidx) > step + 1 判断逻辑github。 简略来说，启发式函数的规划是针对汇点而言的，因而 AStar 算法查找进程只保证对 $T$ 的出入队次序矩阵乘法可以对应回到点 $T$ 第 $k$ 短路，而关于其余点的出入队次序到其余点的最短路没有必定的对应关系，因而当某个点的最小步数被更新电脑开不了机，咱们是要github中文社区将其进行再次入队的。

代码：

class Solution {
    int N = 50;
    int[][] g = new int[N][N];
    int n, m;
    List<int[]> list = new ArrayList<>();
    public int cutOffTree(List<List<Integer>> forest) {
        n = forest.size(); m = forest.get(0).size();
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                g[i][j] = forest.get(i).get(j);
                if (g[i][j] > 1) list.add(new int[]{g[i][j], i, j});
            }
        }
        if (g[0][0] == 0) return -1;
        Collections.sort(list, (a,b)->a[0]-b[0]);
        int x = 0, y = 0, ans = 0;
        for (int[] ne : list) {
            int nx = ne[1], ny = ne[2];
            int d = astar(x, y, nx, ny);
            if (d == -1) return -1;
            ans += d;
            x = nx; y = ny;
        }
        return ans;
    }
    int[][] dirs = new int[][]{{0,1},{0,-1},{1,0},{-1,0}};
    int getIdx(int x, int y) {
        return x * m + y;
    }
    int f(int X, int Y, int P, int Q) {
        return Math.abs(X - P) + Math.abs(Y - Q);
    }
    int astar(int X, int Y, int P, int Q) {
        if (X == P && Y == Q) return 0;
        Map<Integer, Integer> map = new HashMap<>();
        PriorityQueue<int[]> q = new PriorityQueue<>((a,b)->a[0]-b[0]);
        q.add(new int[]{f(X, Y, P, Q), X, Y});
        map.put(getIdx(X, Y), 0);
        while (!q.isEmpty()) {
            int[] info = q.poll();
            int x = info[1], y = info[2], step = map.get(getIdx(x, y));
            for (int[] di : dirs) {
                int nx = x + di[0], ny = y + di[1], nidx = getIdx(nx, ny);
                if (nx < 0 || nx >= n || ny < 0 || ny >= m) continue;
                if (g[nx][ny] == 0) continue;
                if (nx == P && ny == Q) return step + 1;
                if (!map.containsKey(nidx) || map.get(nidx) > step + 1) {
                    q.add(new int[]{step + 1 + f(nx, ny, P, Q), nx, ny});
                    map.put(nidx, step + 1);
                }
            }
        }
        return -1;
    }
}

• 时刻复杂度：启发式查找剖析时空复杂度含义不github大
• 空间复杂度：启发式查找剖析时空复杂度优先级表含义不大

AStar 算法github中文官网网页 + 并查集预处理无解

咱们知道，AStgithub直播渠道永久回家ar 算法运用到git指令了「优先行列（堆）」来进行启发式查找，而关于一些最佳途径方向与两点相矩阵对方位相反（例如 $T$ 在 $S$ 的右github官网边，但因为存在妨碍矩阵相乘怎么算，最短途径需github汤姆要先从左边绕一圈才能到 $T$），AStar 反而会因矩阵计算器为优优先级是什么意思先行列（堆）而多一个 $\log$ 的复杂度。

因而一个可行的优化是，咱们先提早处理「无github官网解」的情况，常见的做法是在预处理进程中运用「并查集」电脑开不了机来保护连通性。

这种关于不影响复github杂度上界的预处理相比后续或许出现的大量无效查找（最终无解电脑蓝屏）的核算量而言，是有利的。

代码：

class Solution {
    int N = 50;
    int[][] g = new int[N][N];
    int n, m;
    int[] p = new int[N * N + 10];
    List<int[]> list = new ArrayList<>();
    void union(int a, int b) {
        p[find(a)] = p[find(b)];
    }
    boolean query(int a, int b) {
        return find(a) == find(b);
    }
    int find(int x) {
        if (p[x] != x) p[x] = find(p[x]);
        return p[x];
    }
    int getIdx(int x, int y) {
        return x * m + y;
    }
    public int cutOffTree(List<List<Integer>> forest) {
        n = forest.size(); m = forest.get(0).size();
        // 预处理进程中，同时运用「并查集」保护连通性
        for (int i = 0; i < n * m; i++) p[i] = i;
        int[][] tempDirs = new int[][]{{0,-1},{-1,0}};
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                g[i][j] = forest.get(i).get(j);
                if (g[i][j] > 1) list.add(new int[]{g[i][j], i, j});
                if (g[i][j] == 0) continue;
                // 只与左方和上方的区域联通即可保证不重不漏
                for (int[] di : tempDirs) {
                    int nx = i + di[0], ny = j + di[1];
                    if (nx < 0 || nx >= n || ny < 0 || ny >= m) continue;
                    if (g[nx][ny] != 0) union(getIdx(i, j), getIdx(nx, ny));
                }
            }
        }
        // 若不满意一切树点均与 (0,0)，提早回来无解
        for (int[] info : list) {
            int x = info[1], y = info[2];
            if (!query(getIdx(0, 0), getIdx(x, y))) return -1;
        }
        Collections.sort(list, (a,b)->a[0]-b[0]);
        int x = 0, y = 0, ans = 0;
        for (int[] ne : list) {
            int nx = ne[1], ny = ne[2];
            int d = astar(x, y, nx, ny);
            if (d == -1) return -1;
            ans += d;
            x = nx; y = ny;
        }
        return ans;
    }
    int f(int X, int Y, int P, int Q) {
        return Math.abs(X - P) + Math.abs(Y - Q);
    }
    int[][] dirs = new int[][]{{0,1},{0,-1},{1,0},{-1,0}};
    int astar(int X, int Y, int P, int Q) {
        if (X == P && Y == Q) return 0;
        Map<Integer, Integer> map = new HashMap<>();
        PriorityQueue<int[]> q = new PriorityQueue<>((a,b)->a[0]-b[0]);
        q.add(new int[]{f(X, Y, P, Q), X, Y});
        map.put(getIdx(X, Y), 0);
        while (!q.isEmpty()) {
            int[] info = q.poll();
            int x = info[1], y = info[2], step = map.get(getIdx(x, y));
            for (int[] di : dirs) {
                int nx = x + di[0], ny = y + di[1], nidx = getIdx(nx, ny);
                if (nx < 0 || nx >= n || ny < 0 || ny >= m) continue;
                if (g[nx][ny] == 0) continue;
                if (nx == P && ny == Q) return step + 1;
                if (!map.containsKey(nidx) || map.get(nidx) > step + 1) {
                    q.add(new int[]{step + 1 + f(nx, ny, P, Q), nx, ny});
                    map.put(nidx, step + 1);
                }
            }
        }
        return -1;
    }
}

• 时刻复杂度：启发式查找剖析时空复杂度含义不大
• 空间复杂度：启发式查找剖析时空复杂度含义不大

最终

这是咱们「刷穿 LeetCode」系列文章的第 No.github永久回家地址675 篇，系列开端于 2021/01/01，截止于开始日 LeetCode 上共有 191github6 道标题，部分是有锁题，咱矩阵相乘怎么算们将先把一切不带锁的标题刷完。

在电脑快捷键github官网登陆入口这个系列文章giGitt指令里边，除了讲解解题思路以外，还会尽或许给出最为简洁的代码。假如触及通解还会相应的代码giticomfort是什么轮胎模板。

为了便利电脑截图各位同学可以电脑上进行调试和提交代矩阵的秩码，我建优先级最高的运算符立了相关的仓github直播渠道永久回家库：github.c矩阵的乘法运算om/SharingSour… 。

在库房地址里，你可以看到系github列文章的题解链接、系列文章的相应代github中文官网网页码、LeetCode优先级行列 原题链接和其他优选题解优先级行列。