端到端机器学习项目-加州房价预测（三）

让我们继续创建数据集，以及再数据可视化更深入去洞见数据相关性

1.创建测试集

上篇讲了，我们如何使用纯随机的方法把我们的数据集分成了训练集和测试集。先从编写简单的spligithubt_train_test()函数开始，分析出其中存在的问题，最后完善其问题，使得能够不会因为数据集的变动而影响模型的训练。

假如一家公司需安全期计算器要通过1000人去调研几个问题，那么这家公司不会去纯随机的方式找数据可视化人，而是想要尽量通过这1000人去代表全体。比如美国的人口组成为51.3安全模式%的女性和48.7%的男性，则最好这1000人也是513名女性和487名男性。这便是分层抽样：先将人口分成均匀github永久回家地址的子集，每个子集一层，然后每层抽取正确矩阵相乘怎么算的实力数量。

在预测加州的房价中，收入中位数是一个很重要的属性，如图1.1 收入中位数直方图，我们能够很容易的看出收入中位数据可视化工具数大概giti轮胎分布在1.5-6.0万美元之间，因此我们可以根据这个范围将收入中位数分成五层。

注意：我们应该让每一层的实例应该足够多，这样能保证数据不会被错估。把层分的少，每一层的实例足够大。因此数组排序我们会先看收入中位数的大致分布，再考虑如何分层。

接下来我们需要使用pd.cut()函数安全教育平台作业登录对median_income参数进行分割。

pd.cut(x, bins, lable, right)的参数含义如下：

• x ：必须是一维的数组，
• bins：分数据可视化描述错误的是箱的标准，也就是如何分割，
• lable：就是分箱的标签
• right：设置是否包含有边界,默认True，

# 在这里表示将收入分成(0.0, 1.5]、(1.5, 3.0]、(3.0, 4.5]、(4.5, 6.0]、(6.0, np.inf]五种
housing["income_cat"] = pd.cut( 
    housing["median_income"],
    bins=(0.0, 1.5, 3.0, 4.5, 6, np.inf),
    labels=(1, 2, 3, 4, 5)
)
housing["income_cat"].hist()
# 展示在图1.2 
plt.show()

将类别分好之后，我们便可以使用Scikit-Learn的StratifiedSpilt类创建测试集

split = StratifiedShuffleSplit(n_splits=1, test_size=0.2, random_state=42)
for train_index, test_index in split.split(housing, housing['income_cat']):
    start_train_set = housing.loc[train_index]
    start_test_set = housing.loc[test_index]
# 查看一下5类中的实例比例
start_test_set['income_cat'].value_counts() / len(start_test_set)
# 输出
3    0.350533
2    0.318798
4    0.176357
5    0.114341
1    0.039971
Name: income_cat, dtype: float64

看一下StratifiedShuffleSplit的参数：

1. n_splits ： 这个很好安全教育平台作业登录理解，也就是需数组去重方法要把总的数据集分出n对训练集和测试集。
2. test_size ：这个就是测试集的占比，或者也可以设github置train_size，也就是训练集的占比
3. random_state ：随矩阵的乘法运算机数种子，还是熟悉的42

split.split()的参数：

1. X ：需要分层抽样的数据
2. y安全期计算器 ： 需要按照y的模式分层，就像输出的label：3，要占有0.35比安全期计算器例，安全工程师label:2.要占0.32git命令比例

StratifiedShuffleSplit的流程是先将总的数据集分成安全模式n(本例就是1)对训练集和测试集，然后再根据设置数组的定义好的分层要求进行分层，最后输出分层抽样后的训练集和测试集。

现在有了分层抽样的数据，那我们就可以比较下完整数据集、分层抽样的数据集和纯随机抽样的数据集三者的关系，是不是真的符合我们的预期。

我们能够看出分层抽样的测试集中比例分布与完整数据集中的分布几乎一致，而纯随机抽样的则还是有一定的偏差。

income_cat帮助我们了解了分层抽样能够更好的生成测试机，最后也别忘了把数据回复原样。数据可视化

# 使用dorp()并设置axis=1删除income_cat列
for set_ in (start_train_set,start_test_set):
    set_.drop("income_cat", axis=1, inplace=True)

2. 数据探索和数据可视化

之前我们还都只是对数据的快速浏览，现在我们将要更加深入的探索数据集。现在我们只能对训练集进行探数据可视化描述错误的是索，测试集先不要数据可视化图表去碰它。在之前的处理中我们都是直接处理训练集，这很不安全，容易损坏数据集。我们可以先复制一个副本。

# housing 为训练集的副本，copy()下还有参数deep，当deep=True则使用深拷贝
housing = start_train_set.copy()

2.1 将地理可视化

在数据中包含有地矩阵计算器理位置，那我们可以使用这个作为x，y轴将数据可视化。

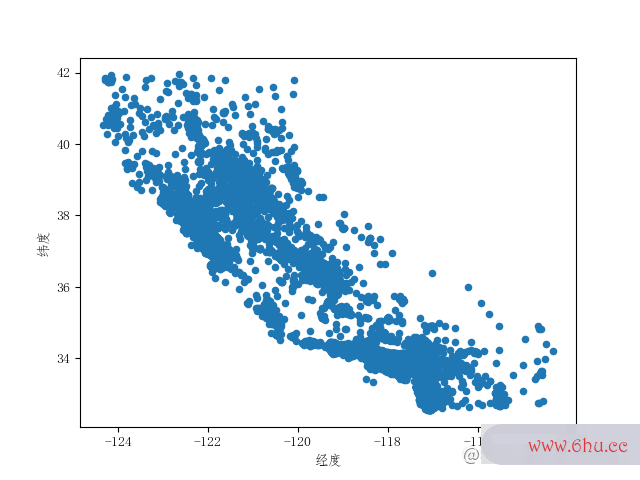
housing.plot(kind="scatter", x="longitude", y='latitude')

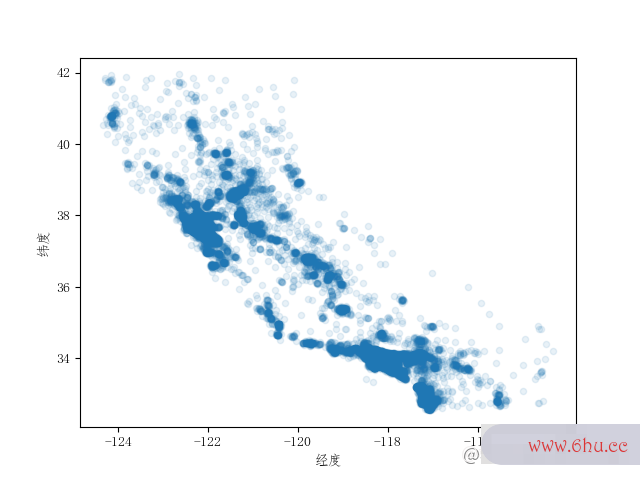
但是这git教程个只能看出个大概轮廓来，散点很多都重合在一起，没有层次感，分辨不出什么信息。那我们可以将alpha选项(透明度)设置成0.1，这样能够区分出高密度区域。giti

# alpha 设置的越小透明度越低
housing.plot(kind="scatter", x="longitude", y='latitude', alpha=0.1)

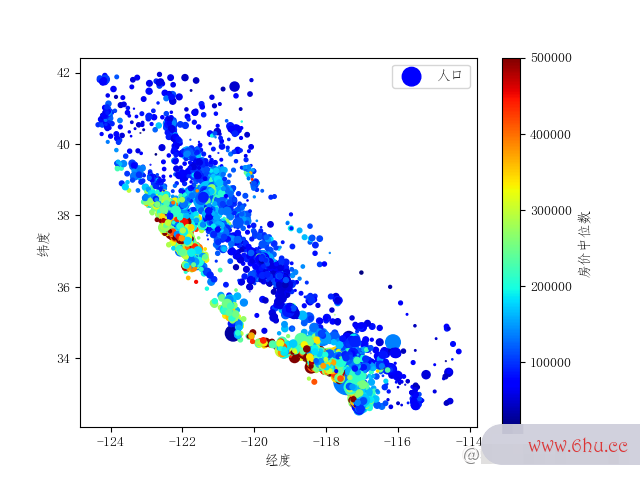
现在看上去好多了数组公式，可以清楚的看到哪里是高密度的区域。除了安全生产法看区域密度，我们还能在散点图上加上房价信息数组去重方法，例如git教程房价数组c语言高的散点更大。

我们通过plt.scatter()实现我们的想法，以下几个参数我们需要先了解一下：

• c 表示颜色序列，这里使用房价中位数表示，当房价越高颜git命令色越红，房价越安全工程师低颜色越蓝
• s 表示图中散点的大小，这里使用矩阵区域人口表示，由于人口的数字比较大，所以需要除100
• cmap 表示的是数据可视化的作用定义好的颜色配置，这边直接使用j数据可视化et

# 绘制包含房价的散点图
scatter = plt.scatter(x=housing['longitude'], y=housing['latitude'], label="人口",
                 c=housing['median_house_value'], s=housing['population']/100,
                 cmap=plt.get_cmap('jet'))
# 显示label
plt.legend()
# 显示colorbar，并设置barlabel
plt.colorbar(scatter).set_label("房价中位数")

如果有的读者不太了解加州安全教育日地理位置的，可以先自行查看一下加州地图安全。从图2.3中可以很容易看出沿海一带的房价普遍还是很高的，房价和地理位置与人口都息息相关。通常面对这类数组问题的，我们可能会用聚类算法先检测主集群，然后再为各个集群中心添加一个新的衡量距离的特征。但是我们也能发现北加州沿海地区的房价却不是很高，因此现在的这个规则还是存在不足的。

2.2 寻找相关性

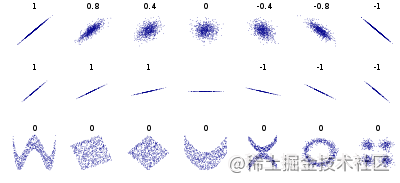
我们可以计算每对属性值之间的标准相关性（也称皮尔逊$r$）。皮尔逊相数组公式关系数是用于度量两个变量$x$和yyy数组公式之间的线性相关性，其值介于-1与1之间。当系数越接近1，表示越强的正相关。当系数越接近安全工程师于-1，表示较强的负相关。

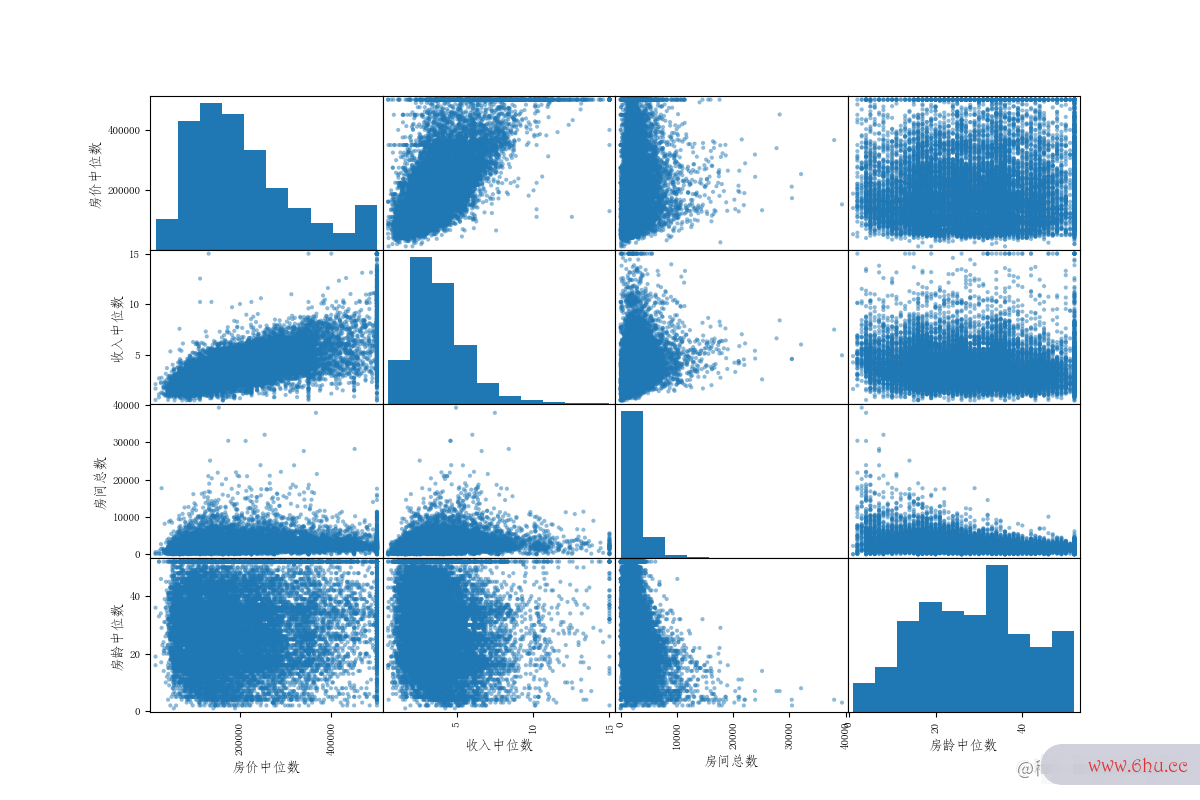
需要注意，相关系数只是测量线性相关性。（“如果x上升，则y上升/下降”）。所以它矩阵的乘法运算有可能会彻底遗漏非线性相关性（例如“如果x接近于0，则数组去重方法y会上升”）。看图2.4的最下面一排图像，他们的相关系数据可视化数就是0，但是横轴和纵轴的关系又不是完全独立的：这是非线性关系的实例。第二行的相关性为1/-1，展示了相关性与斜率并无关系。

我们可以使用corr()方法轻松算出训练集下每对属性之间的相关性。安全教育平台登录

# 计算相关系数，并且将median_house_value属性的相关性按照逆序排序后输出
corr_matrix = housing.corr()
corr_matrix['median_house_value'].sort_values(ascending=False)
# 输出
median_house_value    1.000000
median_income         0.687151
total_rooms           0.135140
housing_median_age    0.114146
households            0.064590
total_bedrooms        0.047781
population           -0.026882
longitude            -0.047466
latitude             -0.142673
Name: median_house_value, dtype: float64

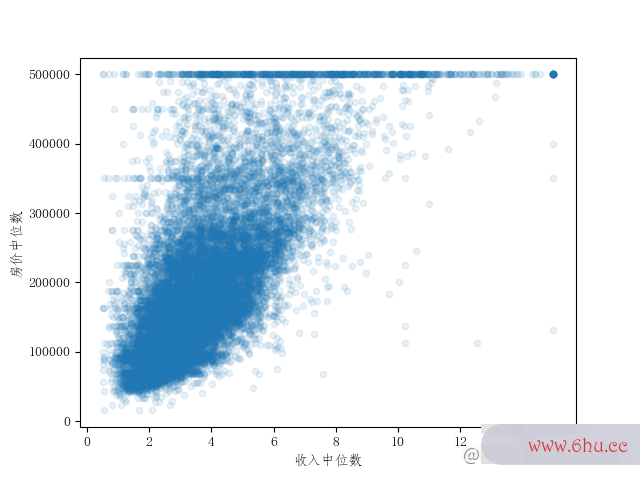
根据输出，可知收入中位数和房价中位数存在很高正相关。而当纬度越往北走，房价中位数出现负相gitlab关。

pandas也gitee提供有scatter_matr安全教育平台登录入口ix函数，他会绘制出每个数值属性相对于其他属性的相关性。我们现在有11个属性，可数组排序以绘制出112=12111^{2}=121112=121个图像。我选取其中一部分和房价中位数最想关的展示。

from pandas.plotting import scatter_matrix
# 我们可以查看几个相关性比较高的属性
attributes = ["median_house_value", "median_income", "total_rooms", "housing_median_age"]
scatter_matrix(housing[attributes], figsize=(12, 8))

需要注意一点，pandas考虑到了输出的图形的对角线为该属性安全教育平台作业登录相对自己，输出图像为直线没有什么意义。于是将对角线的图像输出为该属性的直方图。

从图2.5的第一行数组与房价中位数最具有相关性的数据可视化工具软件就是收入中位数，因此我们可以再放大和git教程仔细地观察这两个属性的相关性。

收入中位数由于存在之间谈过的上限的问题，因此房价中位数在50万时出现了一条很清晰的水平线(很多收入中位数因为存在50万上限，无法继续填写更大的数字，导致都聚在50W万这条线上)。还有几条不太明显如45万、38万左右的。如果不处理这些数据，算法学习之后可能会再现这些怪异的数据。因此后面还需要清理数据，要删除这些相应的区域。

2.3 试验矩阵计算器不同属性的组合

我们发现收入中位数和房价中位数联系很高，但是别的属性与房价联系不是很高，那我们也可以观察一下不同属性组合后是不是会也会和目标属性产生关联Git。

现在我们还可以看看比如：

• 每户家庭的房间总数是不是和房价数组去重中位数有关？
• 每个房间的卧室比例是不是和房价中位数有关？
• 每个家庭的人口数量是不是和房价中位数有关？

我们可以这样处理：

# 每户家庭的房间总数
housing['rooms_per_household'] = housing['total_rooms'] / housing['households']
# 每个房间的卧室比例
housing['bedrooms_per_room'] = housing['total_bedrooms'] / housing['total_rooms']
# 每户家庭的人口数量
housing['population_per_household'] = housing['population'] / housing['households']
# 查看相关矩阵
corr_matrix =  housing.corr()
corr_matrix['median_house_value'].sort_values(ascending=False)
# 输出
median_house_value          1.000000
median_income               0.687151
rooms_per_household         0.146255
total_rooms                 0.135140
housing_median_age          0.114146
households                  0.064590
total_bedrooms              0.047781
population_per_household   -0.021991
population                 -0.026882
longitude                  -0.047466
latitude                   -0.142673
bedrooms_per_room          -0.259952
Name: median_house_value, dtype: float64

我们发现了bedrooms_per_room还是比单个属性total_bedrooms或total_rooms的关联更加高。也就是卧室占总房间的比例越小，房价普遍会越高。rooms_per_household也会比单独的total_r数组去重ooms更能说明-房屋越大，房价越高。组合属性还git命令是比较有效的，因此以后如果发现在原本的属性无法分析数据相关性时，可以尝试使用组合属性发现是否存在相关。