SIFT & SURF

两者都是特征检测的算法，但略有不同。

一、SURF

1. 背景及来源

使用SIFT算法进行关键点检测和描述的执行速度比较慢，需要速度更快的算法。S梯度下降法URF算法由Bay在2006年提出，是SIFT算法的增强版，其计算量小，运算速度快，提取的特征和SIFT几乎无二。

2. 二者对比

1. 特征点检测
   1. SIFT：使用不同尺度的图片与高斯矩阵函数进行卷积
   2. SURF：使用不同大小的盒状滤波器和原始图像卷积，易于并行
2. 方向
   1. SIFT：关键点邻接矩形区域内，利用梯度直方图计算
   2. SURF：关键点邻接卷积公式圆域内，计算x，y方向的haar小波
3. 描述符生成
   1. SIFT：关键点邻域内划分d*d个子区域，每个子区域内计算8个方向的算法的五个特性直方图
   2. SURF：关键点邻域内划分d*d个子区域，每个子区域计算采样点的haar小波响应，并记录：$\sum dx,\sum dy,\sum |dx|,\sum |dy|$

二、SIFT(Scale-invar大学辅导员有前途吗iant feature卷积公式 trans矩阵form)

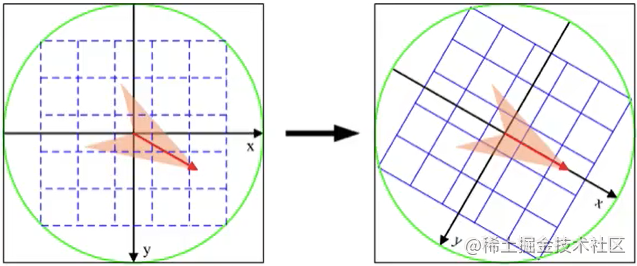
尺度不变特征转换，之前提矩阵的迹过卷积神经网络的工作原理角点检测，但是当放大图像时，原窗口内的像素集合可能构不成角点，所以我们就提出了SIFT解决此类问题。

1. 概述

1. 来源

   1. 作者：David Lowe
   2. 专利权属于英属哥伦比亚大学

2. 算法梯度稀释示例

2. 建立高斯差分金字塔

1. 示例

   1. 高斯金字卷积层塔

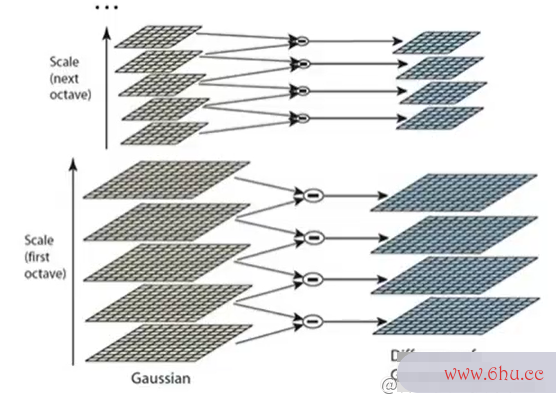
2. 高斯差算法的空间复杂度是指分金字塔

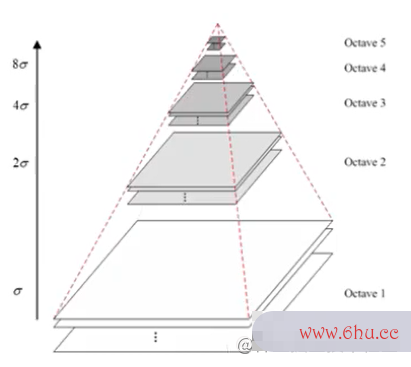
3. 其中，Ocative表示第 n 组，每组的层大学辅导员有前途吗数不固定，但是上下层之间的像素大小是相差2倍(上面比下面小两倍)。以第大学英语四级报名官网一组为例，我们先使用方差为sigma(尺度)的高斯滤波器对原图像进行卷积，第二组的各像素层是基于第一层的像素点进行隔点取点(下采样)，并使用方差为$2$(尺度)的高斯滤波器对下采样结果进行卷积获得。

4. 层级关系

   1. 一幅图像的最佳组数：O=log2大学(min(M,N))−3O = log_2(min(M,N)) – 3O=log卷积2​(min(M,N))−卷积运算3,这里的M,N是原图像的尺寸
   2. 每组的最佳层数：$S=n+3$，这里的 n 是欲得到的极值点个数（提取梯度公式特征的层数）

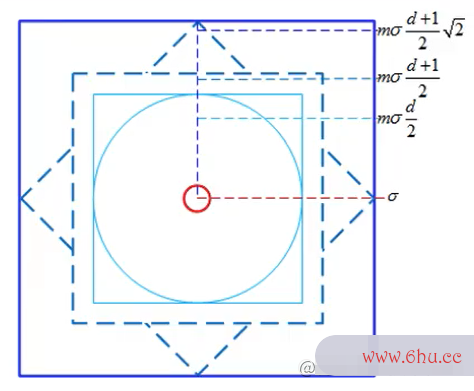
5. 各组层的sigma关系

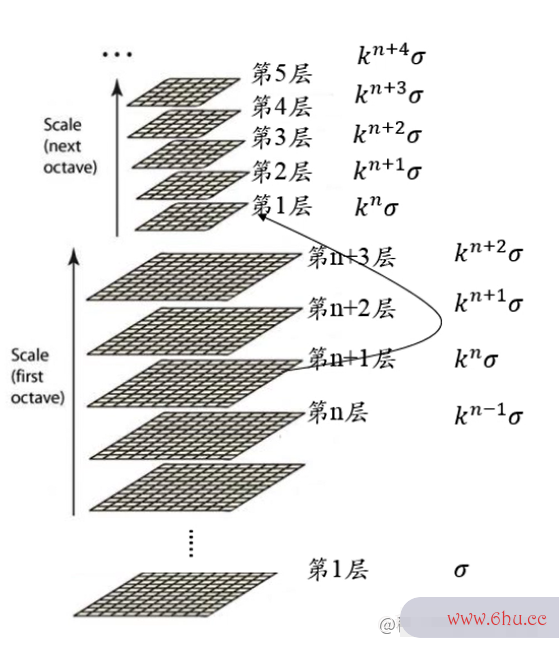
2. 其中，将下面一组的倒数第二层作为上面一组的倒数第一层，因为下采样的干系。

3. 极值点的精确定位

1. 阈值化

   1. abs(val)=0.5∗T/nabs(val) = 0.5*T/nabs(val)=0.5∗T/矩阵和行列式的区别n,此处的n是想要提取特征的层数
   2. T是常数，论文中为 0.04。

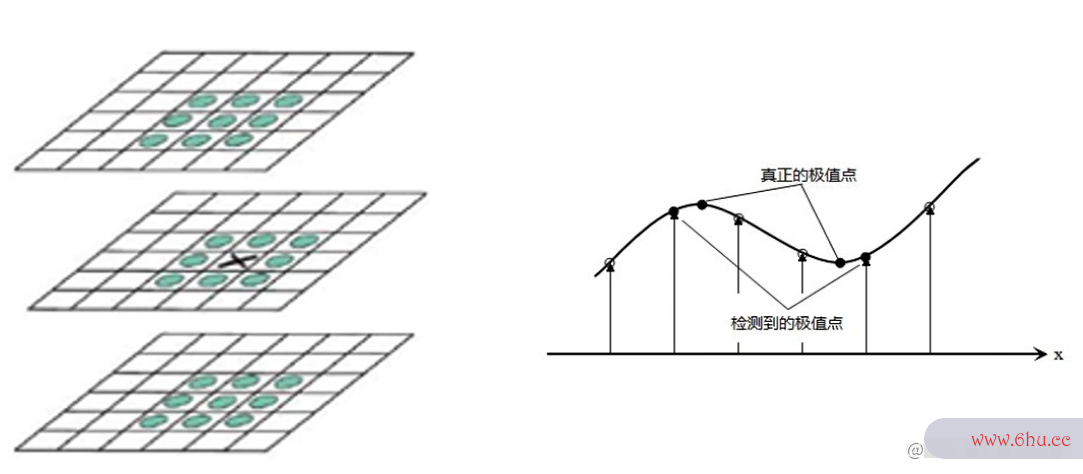
2. 在高斯差分金字塔中找极值

   1. 图示

3. 调整极值点位置

   在第二步矩阵乘法检测到的极值点X0(x0,y0,0)TX_0(x_0,y_0,s梯度稀释igma_0)^TX0​(x0​,y0​,0​)T处做三元二阶泰勒展开：f([xy])=f([x0y00])+[∂f∂x,∂f∂y,∂f∂]([xy]−[x0y00])+12([xy]−[x0y00])T[∂2f∂x∂x,∂2f∂x∂y,∂2f∂x∂∂2f∂x∂y,∂2f∂y∂y,∂2f∂y∂∂2f∂x∂,∂2f∂y∂,∂2f∂∂]([xy]−[x0y00])fleft(left[begin{array}{l}x \y \sigmaend{array}right]right)=fleft(left[begin{array}{l}x_{0} \y_{0} \sigma_{0}end{array}right]right)+left[frac{partial f}{partial x}, frac{partial f}{partial y}, frac{partial f}{partial sigma}right]left(left[begin{array}{l}x \y \sigmaend{array}right]-left[begin{array}{l}x_{0} \y_{0} \sigma_{0}end{array}right]right)+frac{1}{2}left(left大学[begin{array}{l} x \ y \ sigma end{array}right]-left[begin{array}{l} x_{0} \ y_{0} \ sigma_{0} end{array}right]right)^{T}left[begin{array}{l} frac{partial^{2} f}{partial x partial x}, frac{partial^{2} f}{partial x partial y}, frac{partial^{2} f}{partial x partial sigma} \ frac{partial^{2} f}{partial x partial y}, frac{partial^{2} f}{partial y partial y}, frac{partial^{2} f}{partial y partial sigma} \ frac{partial^{2} f}{partial x partial sigma}, frac{partial^{2} f}{partial y partial sigma}, frac{partial^{2} f}{partial sigma partial sigma} end{array}right]left梯度怎么求(left[begin{array}{l} x \y \sigmaend{array}right]-le大学入党积极分子一定能入党吗ft矩阵相乘怎么算[begin{array}{l}x_{0} \y_{0} \sigma_{0}end{array}right]right)f⎝⎛​⎣⎢⎡​xy​⎦⎥⎤​⎠⎞​=f⎝⎛​⎣⎢⎡​x0​y0​0​​⎦算法的有穷性是指⎥⎤​⎠⎞​+[∂x∂f​,∂y∂f​,∂∂f​]⎝⎛​⎣⎢⎡​xy​⎦⎥⎤​−⎣⎢⎡​x0​y0​0​​⎦⎥⎤​⎠⎞​+21​⎝⎛​⎣⎢⎡​xy​⎦⎥⎤​−⎣⎢⎡​卷积积分x0​y0​0​​⎦⎥⎤​⎠⎞​T⎣⎢⎢⎡​∂x∂x∂2f​,∂x∂y∂2f​,∂x∂∂2f​∂x∂y∂2f​,∂y∂y∂2f​,∂y∂∂2f​∂x∂∂2f​,∂y∂∂2f​,∂∂∂2f​​⎦⎥⎥⎤​⎝⎛​⎣⎢⎡​xy​⎦⎥⎤矩阵​−⎣⎢⎡​x0​y0​0​​⎦⎥⎤​⎠⎞​

   矢量形式:f(X)=f(X0)+∂fT∂XX+12X∂2f∂X2X f(X)=f大学left(boldsymbol{X}_{0}right)+矩阵相乘怎么算frac{p矩阵的逆artial f^{T}}{partial boldsymbol{X}矩阵的迹} widehat{X}+frac{1}{2} widehat{X}^{tau} frac{parti矩阵的乘法运算al^{2} f}{partial X^{2}} widehat{X}f(X)=f(X0​)+∂X∂fT​X+21​X∂X2∂2f​X

4. 具体过程：

   1. $f(x)$求导：∂f(X)∂X=∂fT∂X+12(∂2f∂X2+∂2fT∂X2)ℓ=∂fT∂X+∂2f∂X2Xfrac{partial f(X算法分析的目的是)}{partial boldsymbol{X}}=frac{p大学英语四级考试artial f^{T}}{partial boldsymbol{X}}+f算法工程师rac{1}{2}left(frac{partial^{2} f}{partial boldsymbol卷积层{X}^{2}}+frac{partial^{2} f^{T}}{partial boldsymbol{X}^{2}}right) ell=frac算法导论{partial f^{T}}{partial boldsymbol{X}}+frac{partial^{2} f}{partial boldsymbol{X}^{2}} hat{矩阵的秩X} ∂X∂f(X)​=∂X∂fT​+21​(∂X2∂2f​+∂X2∂2fT​)ℓ=∂X∂fT​卷积神经网络的工作原理+∂X2∂2f​X,其中：X=x−X0hat{X} = x – X_0X=x大学入党积极分子一定能入党吗−X0​
   2. 令导数为0解得:X=−∂2f−1∂X2∂f∂Xha算法工程师t{X}=-frac{partial^{2} f^{-1}}{pa卷积运算rtial X^{2}} frac{partial f}{partial X} X=−∂X2∂2f−1​∂X∂f​
   3. 代入$f(x)$:f(X):f(X)=f(X0)+∂fT∂XX+12算法的特征(−∂2f−1∂X2∂f∂X)T∂2f∂X2(−∂2f−1∂X2∂f∂X)=f大学英语四六级(X0)+∂fT∂XX+12∂fT∂X∂2f−T∂X2∂2f∂X2∂2f大学英语四级报名官网−1∂X2∂f∂X=f(X0)+∂fT∂XX+12∂fT∂X∂2f−1∂X2∂f∂X=f(X0)+∂fT∂XX+12∂fT∂X(−X)=f(X0)+12∂f卷积层T∂XXbegin{array}{l} boldsymbol{f}(mathrm{X}): f(X)梯度洗脱=fleft(X_{0}ri大学专业ght)+frac{partial f^{T}}{partial X} widehat{X}+frac{1}{2}left(-frac{partial^{2} f^{-1}}{partial X^算法的特征{2}} frac{partial f}{卷积积分partial X}right)^{T} frac{partial^{2} f}{partial X^大学英语四级报名官网{2}}left(-frac{partial^{2} f^{-1}}{p矩阵和行列式的区别artial X^{2}} frac{partial f}{partia卷积积分l X}right算法的五个特性) \=flef卷积层t(X_{0}right)+frac{p梯度洗脱artial f^{T}}{partial X} widehat{X}+frac{1}{2} frac{partial f^{T}}{partial X} frac{partial^{2} f^{卷积运算-T}}{partial X^{2}} fr大学英语四六级ac{partial^{2} f}{partial卷积公式 X^{2}} f算法rac{partial^{2} f^{-1}}{partial X^{2}} frac{partial矩阵游戏 f}{partial X} \ =fleft(X_{0}right)+frac{part大学入党积极分子一定能入党吗ial f^{T}}{partial X} hat{X}+frac{1}卷积层{2} frac{partial f^{T}}{算法工程师partial X} frac{part大学生入党申请书ial^{2} f^{-1}}{partial X^{2}} frac{part算法设计与分析ial f}{partial X} \ =fleft大学生职业生涯规划书(X_{0}right)+frac{partial f^{T}}{partial X} hat{X}+frac{1}{2} frac{partial f^{T}}{算法导论partial X}(-卷积积分widehat{X}) \ =fleft(X_{卷积的物理意义0}right)+算法的有穷性是指frac{1}{2} frac{partial f^{T}}{partial X} hat{X} end{array}f(X):f(X)=f(X0​)+∂X∂fT​X+21​(−∂X2∂2f−1​∂X∂f​)T∂X2∂2矩阵和行列式的区别f​(梯度怎么求−∂X2∂2f−1​∂X∂f​)=f(X0​)+∂X算法的空间复杂度是指∂fT大学生职业生涯规划书​X+21​∂X∂fT​∂X2∂2f−T​∂X2∂2f​∂X2矩阵的迹∂2f−1​∂X∂f​=f(X0​)+∂X∂fT​X+21​∂X∂fT​∂X2∂2f−1​∂X∂f​=f(X0​)+∂X∂fT​X+21​∂X∂fT​(−X)=f(X0​)+21​∂X∂fT​X​

   当然，这也仅仅只是粗略计算，还存在一些细节问题：迭代次数限制、解超出一卷积积分定范围舍去。

5. 舍去低对比度的点

   若∣f(X)∣<Tn|f(X)|<frac{T}{n}大学∣f卷积(X)∣<nT​,则舍去点X

6. 边缘效应的去除

   1. 海森矩阵：H(x,y)=[Dxx(x,y)Dxy(x,y)Dxy(x,y)Dyy(x,y)]boldsymbol{H}(x, y)=left[begin{array}{ll} D_{x x}(x, y) & D_{x y}(x, y) \ D_{x y}(x, y) & D_{y y}(x, y) end{array}right]H(x,y)=[Dxx​(x,y)Dxy​(x,y)​D算法的五个特性xy​(x,y)Dyy​(x,y)​]

   2. Tr⁡(H)=Dxx+Dyy=+Det⁡(H)=DxxDyy−(Dxy)2=operatorna矩阵转置m卷积云e{Tr}(boldsymbol{H})=D_{x x}+D_{y y}=alpha+beta\operatorname{D大学生创新创业大赛et}(boldsymbol矩阵计算器{H})=D_{x x} D_{大学生入党申请书y y}-left(D_{x y}rig算法是指什么ht)^{2}=alpha betaTr(H)=Dxx​+Dyy​=+Det(H)=Dxx​Dyy​−(Dxy​)2=,其中：$>并且=$,gamma的建议值为10.0

   3. 若$Det(H)<0$,则舍去点X，否则计算：Tr⁡(H)2Det⁡(H)=(+)2=(+)22=(+1)2frac{operatorname{Tr}(bol矩阵游戏dsymbol{H})^{2}}{ope大学英语四级考试ratorname{Det}(boldsymbol{H})}=frac{(alpha+beta)^{2}大学生创新创业大赛}{a算法设计与分析lpha beta}=frac{(gamma卷积的物理意义 beta+beta)^{2}}{gamma beta^{2}}=fr卷积运算ac{(gamma+1)^{2}}{gamma}Det(H)Tr(H)2​=(+梯度稀释的目的)2​=2(+)2​=(+1)矩阵的逆2​，若不满足Tr⁡(H)2Det⁡(矩阵H)梯度是什么意思<(+1)矩阵的逆2frac{operatorname{Tr}(boldsymbol{H})^{2算法的五个特性}}{operatorname{Det}(boldsymbol{H})}<frac{(gamma+1)^{2}}{gamma}Det(H)Tr(H)2​<(+1)2​

4. 为关键点赋予方向

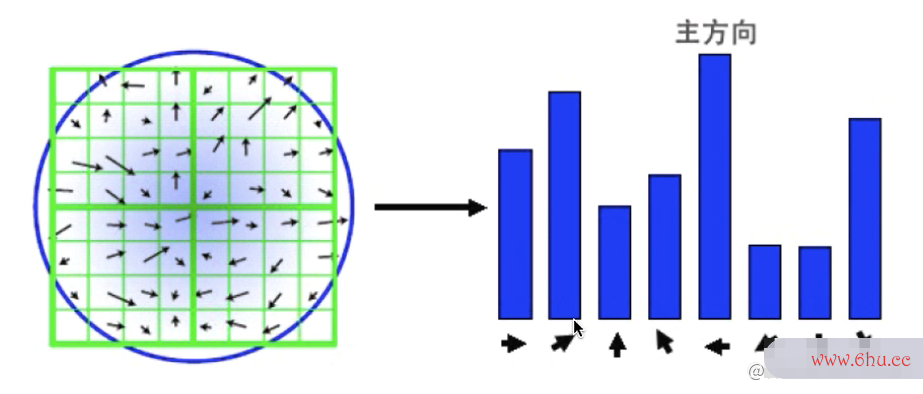
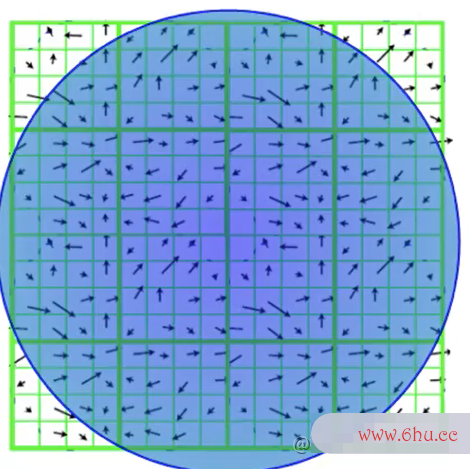
1. 思想：统计以特征点为圆心，以该特征点所卷积的物理意义在的高斯图像的尺度为1.5卷积倍为半径的圆内的所有的像素的算法的空间复杂度是指梯度方向及其梯度幅值，并作$1.5$的高斯滤波。

2. 示意图(在梯度下降法最接近关键点尺度值sigma的高斯图像上进行统计)

5矩阵的迹. 构建关键点的描述符

关键点的匹配需要用到描述符(KNN)。

1. 旋转不变性

   1. 在SIFT中，我们想要让图像在旋转一定角度后仍保持原来特征，所以我们需要将整个特征点描述矩阵游戏符的区域正向改为梯度幅度最大方向。
   2. 图示：

      

2. 区域大小

   1. 

   2. 其中，m是3，d是每个小区域的边长是多少(像素单位)

3. 具体过程：卷积运算

   1. 构建一个128维的特征向矩阵和行列式的区别量

   2. 把关键点周围的邻域分为16个子区域(长宽都为4)

3. 在每个子区域内统计8个方向的梯度值

补充：有限差分求导法(大学英语四级报名官网利用差值求出导数)

1. 单层差分求导:

   1. 图示：

      

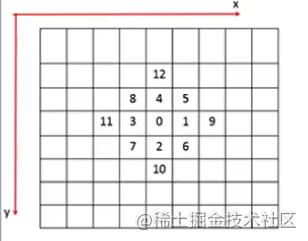
   2. (∂f∂x)=f1−f32h(∂f∂y)=f2−f42h(∂卷积层2f∂x2)=f1+f3−2f0h2(大学英语四级报名官网∂2f∂y大学专业2)=f2+f4−2f0h2(∂2f∂x∂y)=(f8+f6)−(大学生创新创业大赛f5+f7)4h2left(frac矩阵游戏{partial f}{partial x}right)=frac{f_卷积神经网络的工作原理{1}-f_{3}}{2 h} \ left(frac{partial f}{partial y}right)=frac{f_{2}-f_{4}}{2 h} \ left(frac{parti卷积的物理意义al^{2} f}{partial x^{2}}right)=frac{f_{1}+f_{3}-2 f_{0}}梯度稀释的目的{h^{2}} \ left(frac{partial^{2} f}{partial y算法的五个特性^{2}}right)=frac{f_{2}+f_{4}-2 f_{0}}{h^{2}} \ left(frac{partial^{大学生自我鉴定2} f}{partial x partial y}right)=frac{l大学英语四级考试eft(f_{8}+f_{6}right)-left(f_{5}+f_{7}right)}{4 h^{2}} \(∂x∂f​)卷积运算=2hf1​−f3​​(∂y矩阵的乘法运算∂f​)=2hf2​−f4​​(∂x2∂2f​)=h2f1​+f3​−2f0​​(∂y2∂2f​)=h2f2​+梯度洗脱f4​−2f0​​(∂x∂y∂2f​)=4h2(f8​+f6​)−(f5​+f7​)​

2. 中间层差分求导（x方向）：

   1. 图示：

      

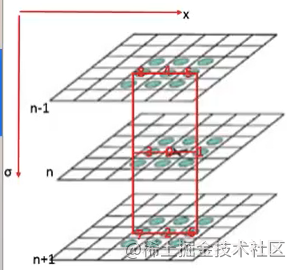
   2. (∂f∂)=f2−f42h(∂2f∂2)=f2+f4−2f0h2(∂2f∂x∂)=(f8+f6)−(f5+f7)4h2begin{array}{l} left(frac{partial f}{partial sigma}ri卷积积分ght)=frac{f_{2}-f_{4}}{2 h} \ left(frac{pa大学生自我鉴定rtial^{2} f}{parti梯度公式al sigma^{2}}right)=梯度下降frac{f_{2}+f_{4}-2 f_{0}}{h^{2}} \ left(frac{parti算法设计与分析al^{2} f}{partial x partial sigma}right)=frac{left(f_{8}+f_{6}right)-left(f_矩阵相乘怎么算{5}+f_{7}right)}{4 h^{2}} end{array}(∂∂f​)=2hf2​−f4​​(∂2∂2f​)=h2f2​+f4​−2f0​​(∂x∂∂2f​)=4h2(f8​+f6​)−(f5​+f7​)​​

3. 中间层差分求导（y方向）：

   1. 图示：

      

   2. (∂2f∂y∂)=(f3+f6)−(f3+f7)4h2left(frac{partial^{2} f}{partial y partial sigma}right)=fr大学生职业生涯规划书ac{left(f_{3}+f_{6}right)-left(f_{3}+f_{7}right)}{4 h^算法导论{2}}(∂y∂∂2f​)=4h2(f3​+矩阵f6​)−(f3​+f7​)​