本文已参加「新人创作礼」活动,一起开启创作之路。
这次带来的是RStudio的进阶图形系统的动态图。
各个知识点后面都有对应的小练习哦,大家可以利用刚刚学到的知识来试着写写看!
动态图
通过http://192.168.1.1登录R包animation可以制作各类动态展示图. 支持gif,mp4,swf,html等格式
- saveGIF
- saveMovie
- savhttp代理eVideo
- saveSWF
- saveHTML
# install.packages("animation")
library(animation)
# saveGIF
# 需要 ImageMagick or GraphicsMagick, 安装时会同时安装'magick'
saveGIF(
{
for(i in 0:99){
x = i*2*pi/100
plot(cos(x), sin(x), xlim=c(-1,1), ylim=c(-1,1),asp=1)
}
}, interval=0.1, ani.width=400, ani.height=400, movie.name="circle.gif"
)
saveGIF(
{
for(i in 1:100){
curve(sin(x), from=-5+(i*0.05), to=5+(i*0.05), col="red", ylab="")
curve(cos(x), from=-5+(i*0.05), to=5+(i*0.05), col="blue", ylab="", add=T)
legend("topright", legend=c("sin(x)","cos(x)"), fill=c("red","blue"), bty="n")
}
}, interval=0.1, ani.width=550, ani.height=350, movie.name="sin_cos.gif"
)
# saveMovie
# saveGIF has an alias saveMovie (i.e. they are identical); the latter name is for compatibility to older versions of this package (< 2.0-2). It is recommended to use saveGIF to avoid confusions between saveMovie and saveVideo.
# saveVideo
# 需要安装 FFmpeg, http://ffmpeg.org/
# FFmpeg is the leading multimedia framework, able to decode, encode, transcode, mux, demux, stream, filter and play pretty much anything that humans and machines have created. It supports the most obscure ancient formats up to the cutting edge. No matter if they were designed by some standards committee, the community or a corporation. It is also highly portable: FFmpeg compiles, runs, and passes our testing infrastructure FATE across Linux, Mac OS X, Microsoft Windows, the BSDs, Solaris, etc. under a wide variety of build environments, machine architectures, and configurations.
saveVideo(
{
for(i in 1:100){
curve(sin(x), from=-5+(i*0.05), to=5+(i*0.05), col="red", ylab="")
curve(cos(x), from=-5+(i*0.05), to=5+(i*0.05), col="blue", ylab="", add=T)
legend("topright", legend=c("sin(x)","cos(x)"), fill=c("red","blue"), bty="n")
}
}, interval=0.1, ani.width=550, ani.height=350, video.name="sin_cos.mp4",
ffmpeg="/Users/tmp/ffmpeg"
)
# 修改 ani.options 方便后续调用
ani.options(ffmpeg = "/Users/tmp/ffmpeg")
# saveHTML
# saveHTML(expr, img.name = "Rplot", global.opts = "", single.opts = "",
# navigator = ani.options("nmax") <= 100 && ani.options("interval") >= 0.05,
# htmlfile = "index.html", ...)
saveHTML(
{
for(i in 1:100){
curve(sin(x), from=-5+(i*0.05), to=5+(i*0.05), col="red", ylab="")
curve(cos(x), from=-5+(i*0.05), to=5+(i*0.05), col="blue", ylab="", add=T)
legend("topright", legend=c("sin(x)","cos(x)"), fill=c("red","blue"), bty="n")
}
}, img.name="sin_cos", htmlfile="sin_cos.html"
)
练习
# Q1
# 画一个连续变动的函数曲线, 比如 y=(x-1)*(x-2), x从0到3连续变化对应的动态图
习题
# Q1
# 画一个螺旋线的动态图
# 螺旋线方程:
# x = t*cos(c*t) # c为某个实数
# y = t*sin(c*t)
# Q2 (选做)
# 之前我们写过clock函数可以绘制出某个静止状态的时钟钟面, 现在要求生成一段动态的时钟视频/图
对重复性的进一步抽象: 递归(数据结构实验报告Recursive)
循环能帮助我们方便的处理重复性的工作, 函数能帮助我们将这一过程固定下来,linux系统安装 更加方便反复调用这一过数据结构程.
递归(Recursive)思想体现了对重复模式的一种新理解:函数会调用自己来完成重复性的工作. 正确运用递归方法的前提是能够很好的理解问题(的抽象结数据结构与算法构).
- 递归思想html简单网页代码
- 递归的例子: 阶乘
- 递归的例子: 快速排序
# 递归思想
# 递归函数会调用自身, 因此, 它体现了一种新的重复: 包含自身结构的重复.
# 递归很抽象, 只有很好的理解了问题的结构, 才能正确的使用递归
# 递归很优雅, 因为它抓住了问题的本质, 经常可以用非常简洁的代码解决问题
# 递归其实是数学归纳法的逆过程
# 递归的例子: 阶乘
factorial(8)
# 原来的写法
my_factorial = function(n){
s = 1
i = 0
while(i < n){
i = i+1
s = i*s
}
return(s)
}
my_factorial(8)
# 递归的写法
my_factorial = function(n){
if(n == 0) return(1)
if(n > 0) return( n*my_factorial(n-1) )
}
my_factorial = function(n){
s = 1
if(n > 0) s = n*my_factorial(n-1)
return(s)
}
my_factorial(8)
# 递归的例子: 快速排序
# 快速排序(Quicksort) 是一种非常经典的排序方法, 也是递归的一个经典例子
# 快速排序的做法如下:
# (1). 对于一个向量x, 取出其第一个元素a
# (2). 将x中小于a的其它元素组成新向量x1, 将x中大于等于a的其它元素组成新向量x2
# (3). 得到新向量x=c(x1, a, x2)
# (4). 在两个子向量x1和x2上继续从(1)开始
qs = function(x){
if(length(x) <= 1) return(x)
a = x[1]
x_left = x[-1]
x1 = x_left[x_left < a]
x2 = x_left[x_left >= a]
return( c(qs(x1), a, qs(x2)) )
}
qs( c(5,4,12,13,3,8,88) )
练习
# Q1
# 我们曾经写过一个函数, 可以创建 Fibonacci 数列的前n项, 现在要求用递归的思想重写这个函数
Fibonacci = function(n){
if(n <= 2) return(rep(1,n))
return( c(Fibonacci(n-1), Fibonacci(n-1)[n-2]+Fibonacci(n-1)[n-1]) )
}
Fibonacci(8)
习题
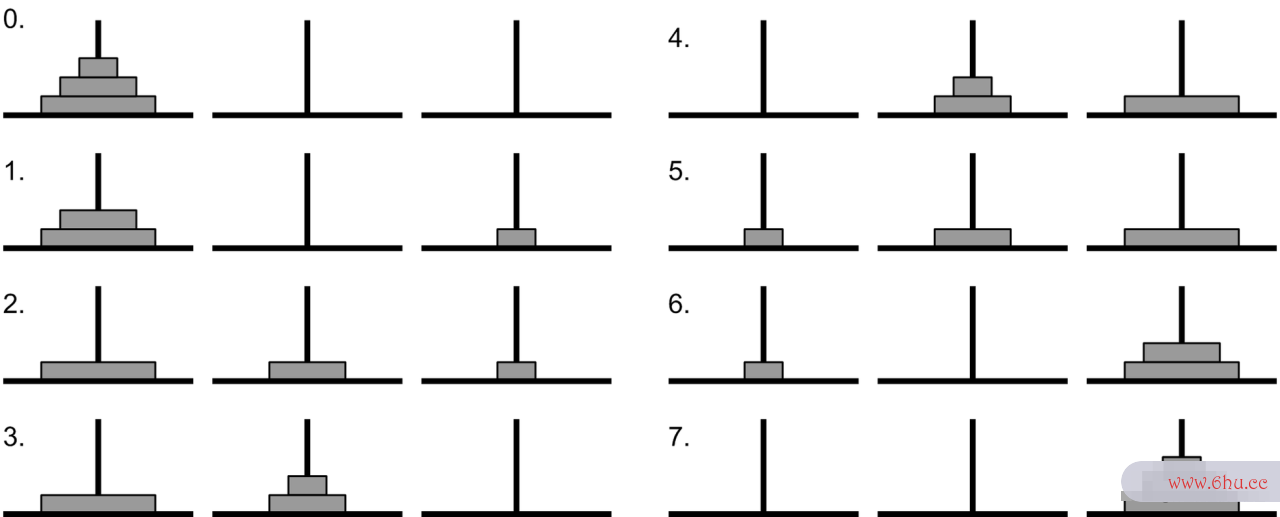
# Q1
# Tower汉诺塔
# 写一个函数, `tower_hanoi(n)` 可返回n阶汉诺塔的解法(无需画图). 思考用何种数据结构可以存储这个解法.
# 相关材料:
# The Tower of Hanoi(汉诺塔) 在1883由法国数学家douard Lucas 发明.
# The Tower of Hanoi (also called the Tower of Brahma or Lucas' Tower[1] and sometimes pluralized as Towers) is a mathematical game or puzzle. It consists of three rods and a number of disks of different sizes, which can slide onto any rod.
#
# The objective of the puzzle is to move the entire stack to another rod, obeying the following simple rules:
#
# 1. Only one disk can be moved at a time.
# 2. Each move consists of taking the upper disk from one of the stacks and placing it on top of another stack or on an empty rod.
# 3. No larger disk may be placed on top of a smaller disk.
# Q2 (选做)
# 将汉诺塔的解法变成一个动态图或视频
3阶汉诺塔的最优解法图示: