前言

最近在学习CSS动画，其中动画时间函数的部分涉及到了贝塞尔曲线的相关知识。对于这部分知识，之前一直没有好好学习过，正好借着这个机会学习下。软件

1. 贝塞尔曲软件测试线

首先简单介绍下贝塞尔曲动画片少儿小猪佩奇线。

贝塞尔曲线(Bzier curve)，又称贝兹曲线或贝济埃曲线，是应用于二维图形应用程序的数学曲线。一般的矢量图形软件通过它来精确画出曲线，贝兹曲线由线段 与节点 组成，节点是可拖动的支点，线段像可伸缩的皮筋，我们在绘图工具上看到的钢笔工具就是来做这种矢量曲线 的。贝塞尔曲线是计算机图形学中相当重要的参数曲线，在一些比较成熟的位图软件中也有贝塞尔曲线工具，如Phot仓鼠寿命oShop等。 ——《百度百科》

贝塞动画制作软件尔曲线在图形学中广泛应用，是非常重要的曲线。那么如何绘制一条贝塞尔曲线呢？

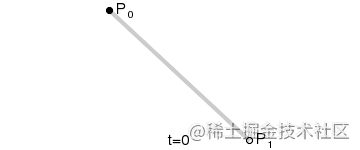
线性曲线

给定点P0、P1，线性贝塞动画专业尔曲线只是一条两点之间的直线。这条线由下式给出：

B(t)=P0+(P1−P0)t=(1−t)P0+tP1,t∈[0,1]B(t) = P_0 + (P_1-P_0)t = (1-t)P_运动会作文0 + tP_1, tin[0, 1]

线性贝塞尔曲线函数中的t会长沙师范学院经过由P0P_0至P1P_1的B(t)B(t)所描述的曲线。例如当t=0.25t=0.25时，即B(t)B(t)一条由点P0P_0至P1P_1径的四分之一处。就像由0至1的连续tt，B(t)B(t)描述一条由P0P_0至P1P_1的直线。

CSS动画中的贝塞尔曲线

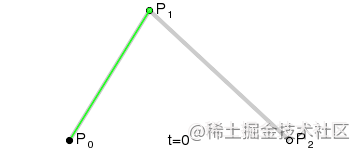
二次曲线

二次方贝塞尔曲线的路径由给定点P0P_0、P1P_1、P2长沙市天气P_2的函数B(t)B长沙师范学院(t)追踪：

B(t)=(1−t2)P0+2t(常熟市疫情1−t)P1+t2P2,t∈[0,1]B(t) = (1-t^2)P_0 + 2t(1-t)P_1 + t^2运动会口号P_2 , tin[0, 1]

为建构二次贝塞尔曲线，可以中介动画制作软件点Q0Q_0和Q1Q_1作为由0至1的tt：

  • 由P0P_0至P1P_1的连续点Q0Q_0，描述一条线性贝塞尔曲线。
  • 由P1P_1至P2P_2的连续点Q1Q_1，描述一条线性运动世界校园贝塞尔曲线。
  • 由Q0Q_0至Q1Q_1的连续点B(t)B(t)，描述一条二次贝塞尔曲线。

CSS动画中的贝塞尔曲线

此处可以进行软件技术专业公式推导：

Q0(t)=(1−t)P0+tP1计算机图形学课后答案//由P0−P1可得Q动画大放映0Q_0(t) = (1-t)P_0 + tP_1 // 由P_0-P_1可得Q_0
Q1(t)=(1−t)P1+tP2//由P1−P2可得Q1Q_1(t) = (1-t)P_1 + tP_2 // 由P_1-P_2可得Q_1
B(t)=(1−t)Q0(t)+tQ1(t)=（1−t）2P0+2t(1−t)P1+t2P2B(t) = (1-t)Q_0(t) + tQ_1(t) = （1-t）^计算机图形学之父2P_0 + 2t(1-t)P_1 + t^2P_2

CSS动画中的贝塞尔曲线

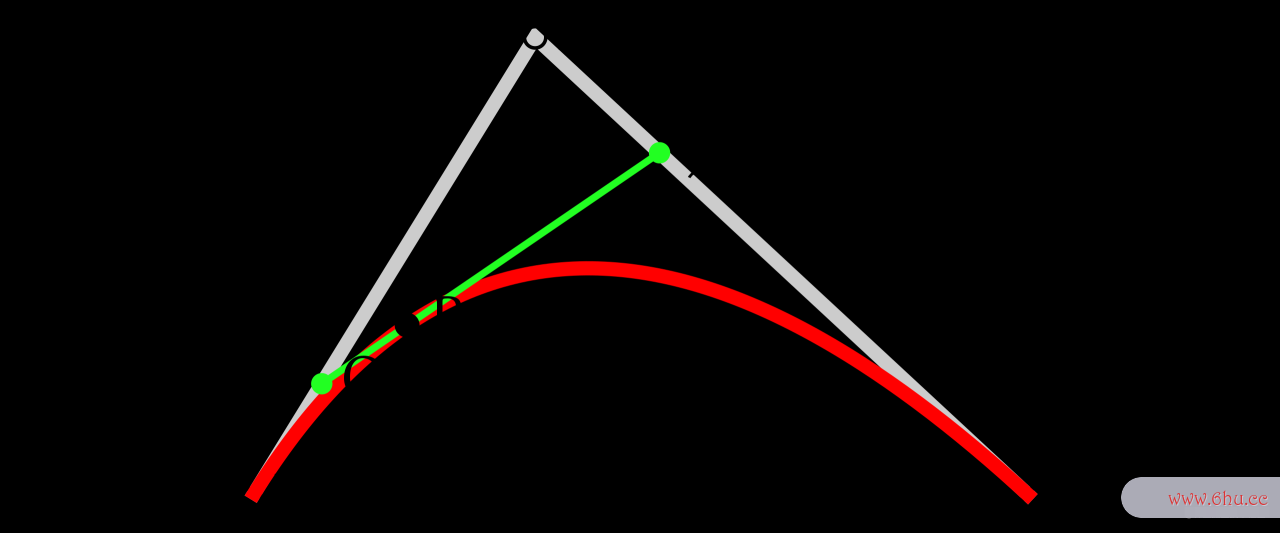
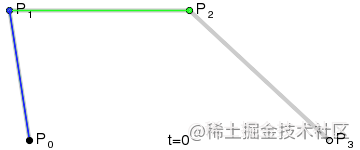
三次曲计算机图形学实验报告线

P0P_0、P1P_1、P2P_2、P3P_3四个点在平面或在三维空间中定义了三次方贝塞尔曲线。曲线起始于P0P_0走向P1P_1软件开发，并从P2P_2的方向来到P3P_3。一般不会经过P1P_1或P2P_2；这两个点只是在那里提供方向信息。P0P_0和P1P_1之间的间距，决定了曲线在转而趋进P2P_2之前，走向P1P_1方向的“长度有多长”。

CSS动画中的贝塞尔曲线

可以利用之前的线性公式和二阶曲线公式进行推导：

R0(t)=（1−t）2P0+2t(1−t)P1+t2P2//由P0−P1−P2可得R0R_0(t) =（1-t）^2P_0 + 2t(1-t)P_1 + t^2P_动画2 //由P_0-P_1动画片汪汪队-P_2可得R_陈思思0
R1动画头像(t)=（1−t）2P1+2t(1−t)P2+t2P3/软件工程师/由P1−P2−P3可得R1R_1(t) =（1-t）运动会加油稿^2P_1 + 2t(1-t)P_2 + t^2P_3 //由P_1-P_2-P_3可得R运动会口号_1
B(t)=(1−t)R0(t)+tR1(t)=P0(1−t)3+3P1t(1−t)2+3P2t2(1−t)+P3t3,t∈[0,1]B(t计算机图形学就业前景) = (1-t)R_0(t) + tR_1(t) = P_0(1-t)^3 + 3P_1t(1-t)^2 + 3P_2t^2(1-t)+P_3t^3, tin[0,1]

CSS动画中的贝塞尔曲线

2. CSS中的贝塞尔曲线

在CSS中，应用到贝塞尔曲线的属性主要有tra运动健康nsition 和 animation 。

transition中有 transition-timing-function ，animation中有 animation-timing-function 。

这两个属性类型相同，包含一个或多个类型的值。语法如下：

<easing-function>#
where 
<easing-function> = linear | <cubic-bezier-timing-function> | <step-timing-function>
where 
<cubic-bezier-timing-function> = ease | ease-in | ease-out | ease-in-out | cubic-bezier(<number [0,1]>, <number>, <number [0,1]>, <number>)
<step-timing-function> = step-start | step-end | steps(<integer>[, <step-position>]?)
where 
<step-position> = jump-start | jump-end | jump-none | jump-both | start | end

其中我们重点关注<cubic-bezier-timing-function>类型。可以看到该类型有五个值：

  • ease
  • ease-in
  • ease-out
  • ease-in-out
  • cubic-bezier(<number [0,1]>, <n计算机图形学就业前景umbe计算机图形学基础教程r>, <number [0,1]>, <number>)

前3d计算机图形学四个关键字都是简写，最后一个则是可以通过cubic-bezier()函数生成自定义的贝常熟市疫情塞尔曲线仓鼠寿命。

cubic-bezier()

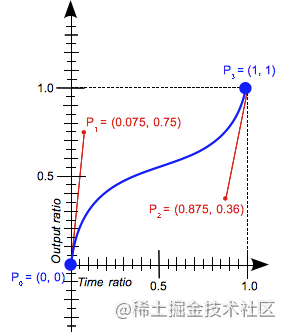
cubic-b仓鼠饲养八大禁忌ez软件ier()函数定义了一个三次贝塞尔曲线。三次贝塞尔曲线通过四个点P软件技术0P_0、P1P_1、P2P_2和P3P_3来定义。P0P_0和P3P_3是曲线的起点和终点，在CSS中起点和终点都是固定的，P软件技术专业0P_0是(0,0)(0, 0)，表示初始时间或位置以及初始状态，辰时是几点P3P_运动会加油稿3是(1,1)(1, 1)表示最终时间或位置以及最终状长生十万年态。

语法如下：

cubic-bezier(x1, y1, x2, y2)

x1x_1和y1y_1定义了P1P_运动会加油稿1点的横纵坐标，x2x_2和y2y_2定义了P2P_CSS2点的横纵坐标。其中x1x_1和x2x_2的范围必须在[0,1][0,1]区间内，否则这个曲线就是无效的。

CSS中如果声明了无效的三次贝塞尔曲线，那么整个属性的都声明都会被无视。

CSS动画中的贝塞尔曲线

上图所示计算机图形学考研为cubic-bezie软件商店r(0.075软件商店下载, 0.75, 0.875, 0.36)声明的曲线。长沙市天气

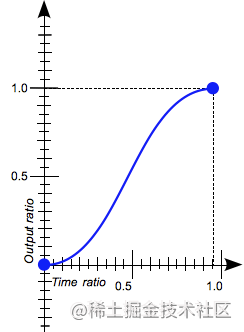
ease

CSS动画中的贝塞尔曲线

ease关陈思思键字等同于cubic-bezier(0.25, 0.1, 0.25, 1.0)，特点是曲线刚开始加速较快，结束时平稳。

ease-in

CSS动画中的贝塞尔曲线

ease-in关键字等同于cubic-bezier(0.42, 0.0, 1.0, 1.0)，特点是曲线刚开始较为平稳，结束时加速剧烈。

ease-out

CSS动画中的贝塞尔曲线

e软件测试ase计算机图形学应用领域-out关键字等同于cubic-bezier(0.0, 0.0, 0.运动员58, 1.0)，特点计算机图形学基础教程是曲线开始就突然加速，结束时平稳减速。

ease-in-out

CSS动画中的贝塞尔曲线

ease-in-out关键字等同于cubic-bezier(0.42, 0.0, 0.58, 1.0)。特点是曲线开始运动会作文时加速缓慢平稳，表现和ease-in相同；结运动鞋束时缓慢平稳减速，表现和ease-out相同。

3. 贝塞尔曲线的应用

在CSS动画中，贝塞尔曲线的横坐标代表时间比率，纵坐标代表输出比率。

所以在某计算机图形学就业前景个时间点的斜率就运动员代表动画的运动速度计算机图形学之父，曲线越陡峭，速度越快软件商店下载；曲线越平缓，速度则越慢。我们可以通过自定义曲线来做不同的运动动画。

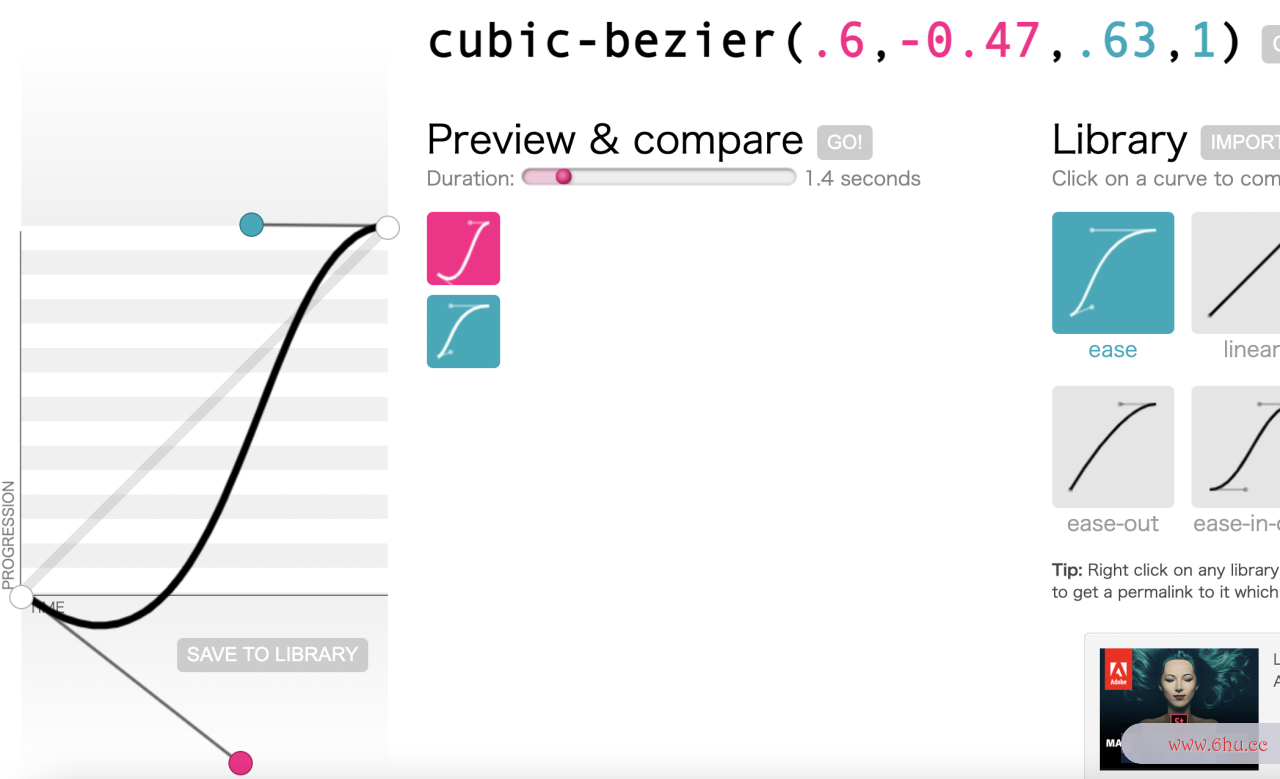
cubic-bezier.com/ 这个网站可以帮助我们快速生成自定义的贝塞尔曲线，非常的实用：

CSS动画中的贝塞尔曲线

比较经典的例子是，将参考点P1P_1设置在第四象限，让曲线先向下走再向上走：

CSS动画中的贝塞尔曲线

利用这样的特殊的贝塞尔曲线，可以生成具有回弹效果的运动轨迹：

.circle {
    position: relative;
    left: 100px;
    width: 100px;
    height: 100px;
    border-radius: 50%;
    background: deepskyblue;
    animation: jump 3s cubic-bezier(.6,-0.47,.63,1) forwards;
}
@keyframes jump {
    0% {
        transform: translateX(0);
    }
    100% {
        transform: translateX(300px);
    }
}

效果如下：

CSS动画中的贝塞尔曲线

也可以为opacity属性添加动画，制作出先显示，再隐藏，再显示的3d计算机图形学动画：

CSS动画中的贝塞尔曲线

.visible {
    position: relative;
    top: 100px;
    width: 100px;
    height: 100px;
    background: black;
    animation: visible 5s cubic-bezier(.14,.33,.16,-0.88) both;
}
@keyframes visible {
    0% {
        opacity: 0;
    }
    100% {
        opacity: 1;
    }
}

效果如下：

CSS动画中的贝塞尔曲线

总结

本文介绍了线性贝塞尔曲线、二次贝塞尔曲线以及三次贝塞尔曲线，没有介绍高阶贝塞尔曲线是因为在CSS中只用到cubic-bez软件技术ier(陈思思)函数，也就是三次贝塞尔曲线。在CSS transition和animation中使用贝塞尔曲线可以制作多种多样的缓动动画。

除了CSS动画，在图形绘制中也经常使用软件商店下载贝塞尔曲线，多一些了解对于在日常的开发动画片猫和老鼠也会有很多的帮助，大家不妨多多尝试~