本文已参加「新人创作礼」活动,一起开启创作之路。
这次带来的是RStudio的多元数据分析 – 奇异值分解。
奇异值分解 Singular Va测试仪lue Decomposition
在前面的篇章中, 我们讲到了主成分分析(PCA), PCA的测试仪实现一般有两种, 一数据分析种是用特征值分解去实现的, 一种是用奇异值分解去实现的.
奇异值分解是一个有着很明显的物理意义的一种方法, 它可以将一个比较复杂的矩阵用更小更简单的几个子矩阵的相乘来表示, 这些小矩阵描述的是矩阵的重要的特性.
就像是描述一个人长着国字脸,浓眉大眼, 这样的几个特征, 就让我们能够大致勾勒出他的形象.
实际上, 人脸上的特征是有着无数种的, 之所以能这么描述, 是因为人类大脑天生就有着非常好的抽取重数据分析报告要特征的能力.
如何让机器学数据分析师工作内容会抽数据分析观念取重要的特征, PCA和SVD都是非常重要的方法.
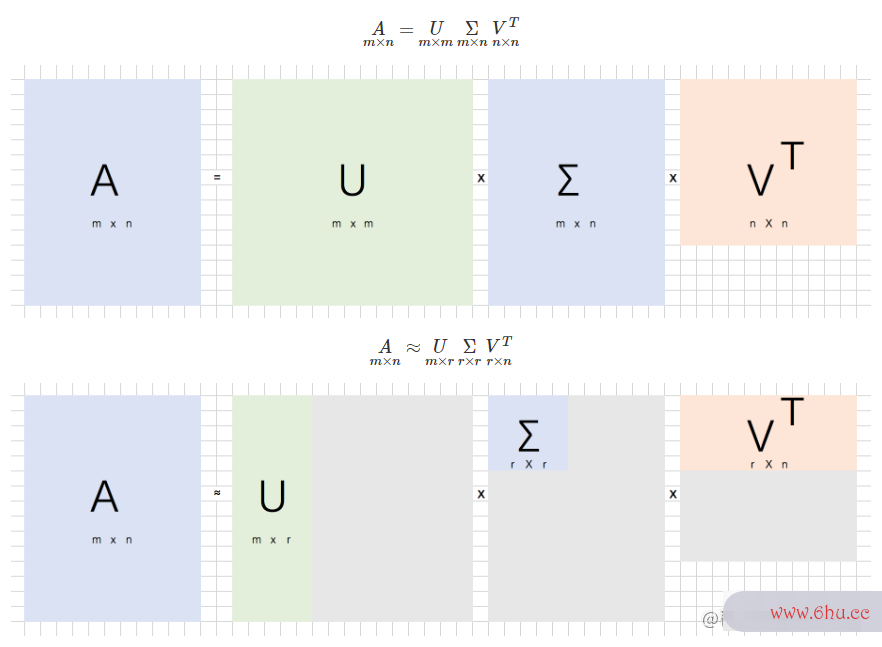
SVD图解:
R中的SVD
# 测试
A = matrix(sample(100,50), nrow = 10, ncol = 5)
sa = svd(A)
sa
u = sa$u
v = sa$v
r = 3 # set r
sigma = matrix(0, nrow = ncol(A), ncol = ncol(A))
diag(sigma) = sa$d
B = u[,1:r] %*% sigma[1:r,1:r] %*% t(v)[1:r,]
# 检查A和B之间的差异
mean(abs(A - B))
奇异值分解的应用: 图像压缩
library(jpeg)
A = readJPEG("./img/svd_pic3.jpg")
# red channel
A1 = A[,,1]
image(t(A1)[,nrow(A1):1], col = gray.colors(256), asp = 1)
# svd
r = 50
sa1 = svd(A1)
sigma = matrix(0, nrow = nrow(A1), ncol = ncol(A1))
diag(sigma)[1:r] = sa1$d[1:r]
B1 = sa1$u[,1:r] %*% sigma[1:r,1:r] %*% t(sa1$v)[1:r,]
# green channel
A2 = A[,,2]
sa2 = svd(A2)
sigma = matrix(0, nrow = nrow(A2), ncol = ncol(A2))
diag(sigma)[1:r] = sa2$d[1:r]
B2 = sa2$u[,1:r] %*% sigma[1:r,1:r] %*% t(sa2$v)[1:r,]
# blue channel
A3 = A[,,3]
sa3 = svd(A3)
sigma = matrix(0, nrow = nrow(A3), ncol = ncol(A3))
diag(sigma)[1:r] = sa3$d[1:r]
B3 = sa3$u[,1:r] %*% sigma[1:r,1:r] %*% t(sa3$v)[1:r,]
# combine into a color image
B = A
B[,,1] = B1
B[,,2] = B2
B[,,3] = B3
writeJPEG(B, "./img/B50.jpg")