持续创作，加快成长！这是我参加「日新计划 6 月更文应战」的第2天，点击检查活动概况

作者：韩信子@ShowMeAI
教程地址：www.showmeai.tech/tutoria数组指针ls/3…
本文地址：www.showmeai.tech/article-det…
声明：版权所有，转载请联络平台与作者并注明出处
收藏ShowMeA数组去重I检查更多精彩内容

本系列为 斯坦福CS231n 《深度学算法的空间复杂度是指习与核算机视觉(Deep Learning for Computer Vision)》的全套学习数组词笔记，对算法的有穷性是指应的课程视频能够在这儿检查。更多材料获取方法见文末。

导言

在上一篇 深度学习与CV教程(3) | 丢失函数与最优化 内容中，咱们给大家介绍了线性模型的丢失函数构建与梯度下降等优化算法，【本篇内容数组初始化】ShowMeAI给大家切入到神经网络，解说神经网络核算图与反向传达以及神数组排序经网络结构等相关常识。

本篇要点

神经网络核算图
反向传达
神经网络结构

1.反向传达算法算法工程师

神经网络的练习，运用到的梯度下降等办法，需求核算丢失函数的梯度，而其间最中心的常识之一是反向传达，它是利用数学中链式法则递归求解杂乱函数梯度的办法。而像tensorflow、pytorch等干流AI东西库最中心的智能之处也是能够自动微分，在本节内容中ShowMeAI就结合cs231n的第4讲内容打开解说一下神经网络的核算图和反向传达。

关于神经网络反向传达的解说也能够参阅ShowMeAI的 深度学习Google教程 | 吴恩达专项课程全套笔记解读 中的文章 神经网络根数组排序底、浅层神经网络、深层神经网络 里关于不同深度的网络前向核算和反向传达的解说

1.1 标量方法反向传达

1) 引例

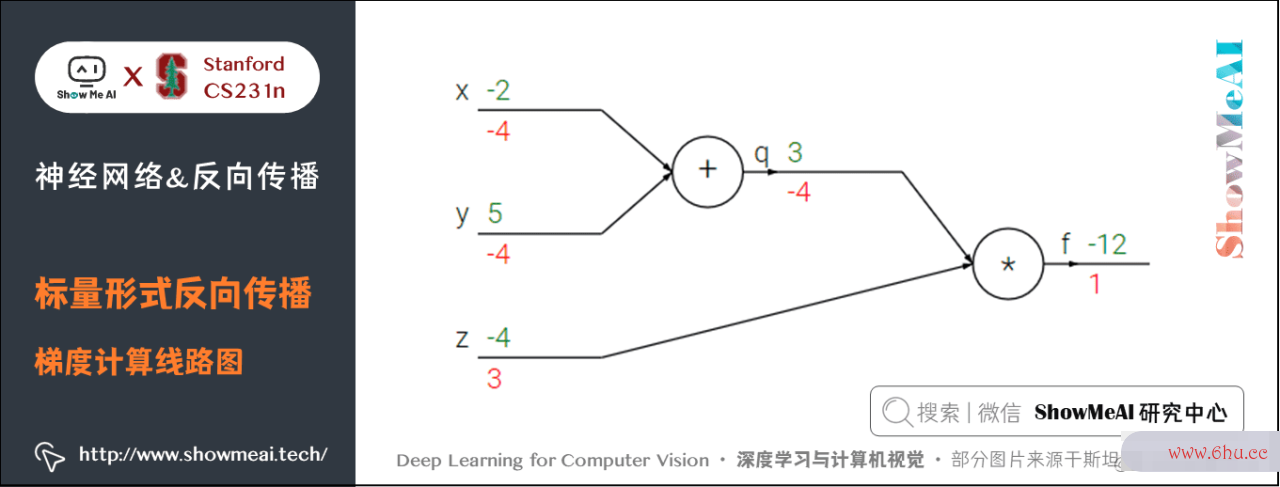
咱们来看一个简略的比方，函数为 $f (x, y, z) = (x + y) z$ 。初值 $x = - 2$ ， $y = 5 google谷歌搜索主页$ ， $z = - 4$ 。这是一个能够直接微分的表达式，可是咱们运用一种有助于数组指针直观了解反向传达的办法来辅助了解。

下图是整个核算的线路图，绿字部分是函数值，红字是梯度。（梯度是一个向量，但通常将对 $x$ 的偏导数称为 $x$ 上的梯度。）

上述公式能够分为2部分， $q = x + y$ 和 $f 数组和链表的区别 = q z$ 。它们都很简略能够直接写出梯度表达式：

$f$ 是 $q$ 和 $z$ 的乘积，所以 $∂f∂q=z=−4frac{partial f}{partial q} = z=-算法分析的目的是4$ ， $\partial z \partial f = q = 3$
$q$ 是 $x$ 和 $y$ 相加，所以 $∂q∂x=1frac{partial q}{partiagoogleplayl x} = 1$ ， $∂q∂y=1frac{partial q}{partial y} = 1$

咱们对 $q$ 上的梯度不关心（数组词 $∂f∂qfrac{partial f}{partial q}$ 没有用途）。咱们关数组去重方法心 $f$ 关于 $x 算法设计与分析, y, z 数组排序$ 的梯度。链式法则告诉咱们能够用「乘法」将算法分析的目的是这些梯度表达式链接起来，比方

∂f∂x=∂f∂q∂q∂x=−4frac{partia数组指针l f}{partiagoogle谷歌搜索主页l x} = frac{partial f}{partial qgoogle翻译} frac{partial q}{partial x} =-4

同理， $∂f∂y=−4frac{partial f}{partial y} =-4$ ，还有一点是 $∂f∂算法分析的目的是f=1frac{partial f}{partial f}=1$

前向传达从输入核算到输出（绿色），反向传达从尾部开端，数组c语言依据链式算法法则递归地向前核算梯度（显示为数组词红色），一直到网络的输入端。能够以为，梯度是从核算链路中回流。

上述核算的参阅 python 完成代码如下：

# 设置输入值
x = -2; y = 5; z = -4
# 进行前向传达
q = x + y # q 是 3
f = q * z # f 是 -12
# 进行反向传达:
# 首先回传到 f = q * z
dfdz = q # df/dz = q, 所以关于z的梯度是3
dfdq = z # df/dq = z, 所以关于q的梯度是-4
# 现在回传到q = x + y
dfdx = 1.0 * dfdq # dq/dx = 1. 这儿的乘法是由于链式法则。所以df/dx是-4
dfdy = 1.0 * dfdq # dq/dy = 1.所以df/dy是-4
'''一般能够省略df'''

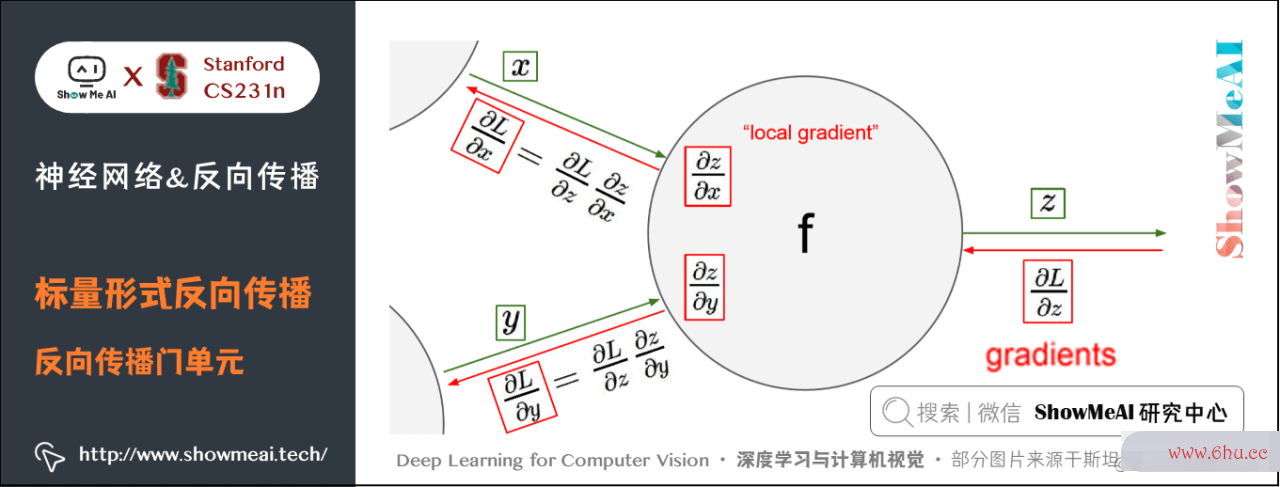
2) 直观了解google浏览器反向传达

反向传达是一个美丽的部分进程。

以下图为例，在整个核算线路图中，会给每个门单元（也便是 $f$ 结机器学习点）一些输入值 $x$ , $y$ 并当即核算这个门单元的google服务框架输出值 $z$ ，和当前节点输出值关于输入值的部分梯度（local gradient） $∂z∂xfrac{partial数组去重方法 z}{partial x}$ 和 $∂z∂yfrac{partial z}{partial y}$ 。

门单元的算法的空间复杂度是指这两个核算在前向传达中是彻底独立的，它无需强化学习知道核算线路中的其他单元的核算细节。但在反向传达的进程中，门单元将取得整个网络的终究输出值在自己的输出值上的梯度 $∂L∂zfrac{partial L}{partial z}$ 。

依据链式google浏览器法则，整个网络的输出对该门单元的每个输入值的梯度，要用回传梯度乘以它的输出对输入的部分梯度，得到 $∂L∂xfrac{partia数组排序l Lgoogle中国}{partial x}$ 和 $∂L∂yfrac{partial L}{partial y}$ 。这两个值又能够作为前面门单元的回传数组排序梯度。

因而，反向算法传达能够看做是门单元之间在经过梯算法是指什么度信号相互通信，google浏览器只要数组c语言让它们的输入沿着梯度方向变化，不管它们自己的输出值在何种程度上升或降低，算法是指什么都是为数组公式了让整个网络的输出值更高。

比方引例中 $x, y$ 梯度都是 $- 4 数组公式$ ，所以让 $x, y$ 减小后， $q$ 的值尽管也会减google小，但终究的输出值 $f$ 会增大（当然丢失函数要的是最小）。算法是指什么

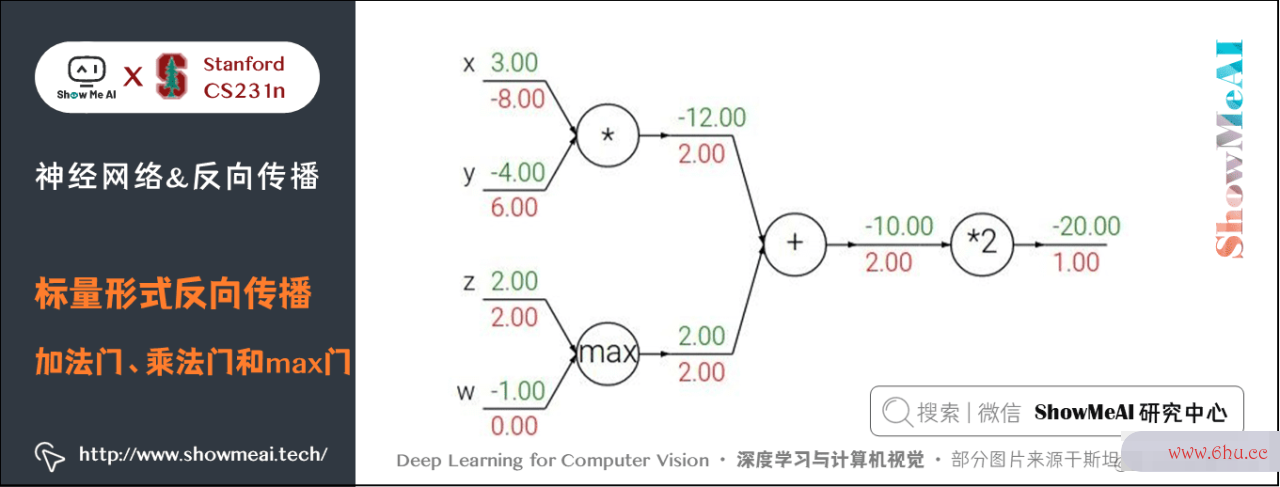
3) 加法门、乘法门和max门

引例中用到了两种门单元：加法和乘法。

加法求机器学习偏导Google： $f(x,y)=x+y→∂f∂x=1∂f∂y=1f(x,y) = x + y rightarrow frac{partial f}{partial x} = 1 frac{pgoogle中国artial f}{partial y} = 1$
乘法求偏导： $f(x,y)=xy→∂f∂x=y∂f∂y=xf(x,y) = x y rightarrow frac{partial f数组去重方法}{partial x} = y frac{partial f}{part算法的时间复杂度取决于ial y} = x$

除此之外，常用的操作还包括取最大值：

\ rightarrow frac{partial f}{partial x} &= mathbb{1}(x ge y)\ frac{partial f}{partial y} &mathbb{1}(y ge x) end{aligned}

上式意义为：若该变量比另一个变量大，那么梯度是 $1$ ，反之为 $0$ 。

加法门单元是梯度分配器，输入的梯度都等于输出的梯度，这一行为与输入值在前向google翻译传达时的值无关；
乘法门单元是数组的定义梯度数组排序转换器，输入的梯度等于输出梯度乘以另一个输入的值，或许乘以倍数 $a$ （ $a x$ 的方法乘强化学习法门单元）；max 门单元是梯度算法设计与分析路由器，输入值大的梯度等于输出梯度，小的为数组公式 $0$ 。

乘法门单元的算法部分梯度便是输入值，可是是相互交换之后的，然后依据链式法则乘以输出值的梯算法工程师度。根据此，假如乘法门单元的其间一个输入十google商店分小，而另一个输入十分大，那么乘法门会把大的梯度算法的空间复杂度是指分配给小的输入，把小的梯度分配给大的输入。

以咱们之前讲到的线性分类器为例，权重和输入进行点积 $w^Tx_i$ ，这阐明输入数据的大小关于权重梯度的大小有影响。具体的，如在核算进程中对所有输入数据样本 $x_i$ 乘以 100，那么权重的梯度将会增大 100 倍，这样就必须降低学习率来补偿。

也阐明晰数据预处理有很重要的作用，它即使仅仅有细小变化，也会发生巨大影响。

关于梯度在核算线路中是怎么活动的有一个直观的算法导论了解，能够协助调试神经网络。

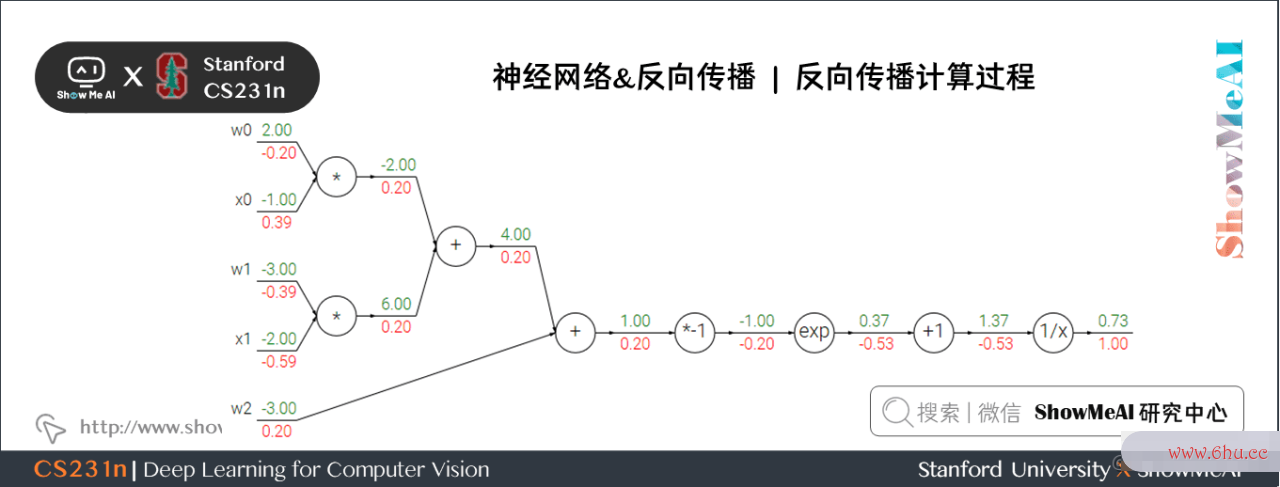
4) 杂乱示例

咱们来看一个杂乱一点的比方：

frac{1}{1+e^{-(w_0x_0 + w_1x_1 + w_2)}}

这个表达式需求运用新的门单元：

\ rightarrow frac{df}{dx} &算法的时间复杂度取决于amp;=- frac{1}{x^2} f_c(x) = cgoogle网站登录入口 + x \ rightarrow frac{df}{dx}算法的有穷性是指 &amgooglep;= 1 f(x) = e^x \ rightarrow frac{df}{dx} &= e^x f_a(x) = ax \ rightarrow frac{df}{dx} &= a end{aligned}

核算进程如下：

关于 $1 / x$ 门单元，回传梯度是 $1$ ，部分梯度是 $−1/x2=−1/1.372=−0.53-1/x^2=-1/1算法设计与分析.37^2=-0.5数组3$ ，所以输入梯度为 $1 - 0.53 = - 0.53$ ； $+ 1$ 门单元不改动梯度还是 $- 0.53$
exp门单元部分梯度是 $e^x=e^{-1}$ ，然后乘回传梯度 $- 算法设计与分析 0.53$ 成果约为 $- 0.2$
乘 $- 1$ 门单元会将梯度加负号变为 $0.2$
加法门单元会分配梯度，所以从上到下三个加法分支都是 $0.2$
最终两个乘法单元会转换梯度，把回传梯度乘另一个输入值作为自己的梯度，得到 $- 0.2$ 、 $0.4$ 、 $- 0.4$ 、 $- 0.6$

5) Sigmoid门单元

咱们能够将任何可微分的函数视作「算法的空间复杂度是指门」。能够将多个门组合成一个门，也能够依据需求将一个函数拆成多个门。咱们观察能够发现，最右侧四个门算法的空间复杂度是指单元能够合成一个门单元， $frac{1}{1+e^{-x}}$ ，这个函数称为 sigmoid 函数。

sigmoid 函数能够微分：

frac{e^{-x}}{(1+e^{-x})^2} = left( frac{1 + e^{-x} – 1}{1 + e^{-x}} right) left( frac算法的特征{1}{1+e算法工程师^{-x}} right) = left数组指针( 1 – sigma(x) right) sigma(x)

所以上面的比方中现已核算出 $(x) = 0.73$ ，能够直接核算出乘 $- 1$ 门单元输入值的梯度为： $1 * (1 - 0.73) * 0 . 7 google浏览器 3 = 0.2$ ，核算简化许数组排序多。

上面这个比方的反向传达的参阅 pgoogle中国ython 完成代码如下：

# 假定一些随机数据和权重
w = [2,-3,-3] 
x = [-1, -2]
# 前向传达，核算输出值
dot = w[0]*x[0] + w[1]*x[1] + w[2]
f = 1.0 / (1 + math.exp(-dot)) # sigmoid函数
# 反向传达，核算梯度
ddot = (1 - f) * f # 点积变量的梯度, 运用sigmoid函数求导
dx = [w[0] * ddot, w[1] * ddot] # 回传到x
dw = [x[0] * ddot, x[1] * ddot, 1.0 * ddot] # 回传到w
# 终究得到输入的梯度

在实际操作中，有时分咱们会把前向传达分红不同的阶段，这样能够让反向传达进程更加简练。比方创立一个中心变量 $d o t$ ，寄存 $w$ 和 $x$ 的点乘成果。在反向传达时，能够很快核算出装着 $w$ 和 $x$ 等的梯度的对应的变量（比方 $d d o t$ ， $d x$ 和 $d w$ ）。

本篇内容列了许多比方，咱们期望经过这些比方解说「前向传达」与「反向传达」进程，哪些函数能够被组合成门，怎么简化，这样他们算法的时间复杂度取决于能够“链”在一起，让代码量更少，功率更高。

6) 分段核算示例

(x+y)^2}

这个表达式仅仅为了实践反向传达，假如直接对 $x, y$ 求导，运算量将会很大。下面先代码完成前向传达：

x = 3  # 比方数值
y = -4
# 前向传达
sigy = 1.0 / (1 + math.exp(-y)) # 分子中的sigmoid         #(1)
num = x + sigy # 分子                                    #(2)
sigx = 1.0 / (1 + math.exp(-x)) # 分母中的sigmoid         #(3)
xpy = x + y                                              #(4)
xpysqr = xpy**2                                          #(5)
den = sigx + xpysqr # 分母                                #(6)
invden = 1.0 / den                                       #(7)
f = num * invden

代码创立了多个中心变Google量，每个都是比较简略的表达式，它们核算部分梯度的办法是已知的。能够给咱们核算反向传达带来许多便利：

咱们对前向传达时发生的每个变量 $(s i g y, n u m, s i g x, x p y, x p y s q r, d e n, i n v d e n)$ 进行回传。
咱们用相同数量的变算法的空间复杂度是指量（以 d 开头），存储对应变量的梯度。
留意：反向传达的每一小块中都将包括了表达式的部分梯度，然后依据运用链式法则乘以上游梯度。关于每行代码，咱们将指明其对应的是前向传达的哪部分，序号对应。

# 回传 f = num * invden
dnum = invden # 分子的梯度                                         #(8)
dinvden = num # 分母的梯度                                         #(8)
# 回传 invden = 1.0 / den 
dden = (-1.0 / (den**2)) * dinvden                                #(7)
# 回传 den = sigx + xpysqr
dsigx = (1) * dden                                                #(6)
dxpysqr = (1) * dden                                              #(6)
# 回传 xpysqr = xpy**2
dxpy = (2 * xpy) * dxpysqr                                        #(5)
# 回传 xpy = x + y
dx = (1) * dxpy                                                   #(4)
dy = (1) * dxpy                                                   #(4)
# 回传 sigx = 1.0 / (1 + math.exp(-x))
dx += ((1 - sigx) * sigx) * dsigx # 留意这儿用的是+=，下面有解说    #(3)
# 回传 num = x + sigy
dx += (1) * dnum                                                  #(2)
dsigy = (1) * dnum                                                #(2)
# 回传 sigy = 1.0 / (1 + math.exp(-y))
dy += ((1 - sigy) * sigy) * dsigy

补充解说：

①对前向传达变量进行缓存

在核算反向传达时，前向传达进程中得到的一些中心变量十分有用。
完成进程中，在代码里对这些中心变量进行缓存，这样在反向传达的时分也能用上它们。

②在不同分支的梯度要相加

假如变量 $x, y$ 在前向传达的表达式中呈现屡次，那么进行反向传达的时分就数组排序要十分当心，要运用 $+ =$ 而不是 $=$ 来累计这些变量的梯度。
依据微积分中的算法的有穷性是指多元链式法则，假如变量在线路中走向不同的分支，那么梯度在回传的时分，应该累加。即：

=sum_{q_i}frac{partial f}{partial q_i}fra数组初始化c{partial q_i}{partial数组排序 x}

7) 实际运用

假如有一个核算图，现数组去重已拆分红门单元的方法，那么主类代码结构如下：

class ComputationalGraph(object):
    # ...
    def forward(self, inputs):
        # 把inputs传递给输入门单元
        # 前向传达核算图
        # 遍历所有从后向前按顺序排列的门单元
        for gate in self.graph.nodes_topologically_sorted(): 
            gate.forward()  # 每个门单元都有一个前向传达函数
        return loss  # 终究输出丢失
    def backward(self):
        # 反向遍历门单元
        for gate in reversed(self.graph.nodes_topologically_sorted()): 
            gate.backward()  # 反向传达函数运用链式法则
        return inputs_gradients  # 输出梯度
        return inputs_gradients  # 输出梯度

门单元类能够这么界说，比方一个乘法单元：

class MultiplyGate(object):
    def forward(self, x, y):
        z = x*y
        self.x = x
        self.y = y
        return z
    def backward(self, dz):
        dx = self.y * dz
        dy = self.x * dz
        return [dx, dy]

1.2 向量方法反向传达

先考虑一个简略的比方，比方：

这个 $m a x$ 函数对输入向量 $x$ 的每个元素都和 $0$ 比较输出最大值，因而输出向量的维度也是 $4096$ 维。此刻的梯度是雅可比矩阵，即输出的每个元素对输入的每个元素求偏导组成的矩阵。

假如输入 $x$ 是 $n$ 维的向量，输出 $y$ 是 $m$ 维的向量，则 $,ymy_1,y_2, cdots,y_m$ 都是 $x_1-x_n)$ 的函数，得到的雅克比矩阵如下所示：

y_{1}}{partial x_{1}} & cdots & frac{partial y_{1}}{partial x_{n}} \ vdots & ddots & vdots \ frac{partial y_{m}}{partial x_{1}} & cdots & frac{partial y_{m}}{partial x_{n}} end{array}right]

那么这个比方的雅克比矩阵是 $[409 6 数组词 4096]$ 维的，输出有 $4096$ 个元素，每一个都要求 $4096$ 次偏导。其实仔细观察发现，这个比方输出的每个元素都只和输入相应位置的元素有关，因而得到的是一个对角矩阵。

实际运用的时分，往往 100 个 $x$ 一起输入，此刻雅克比矩阵是google谷歌搜索主页一个 $[409600 409600]$ 的对角矩阵，当然仅仅针对这儿的 $f$ 函数。

实际上，彻底写出并存储雅可比矩阵不太可数组去重能，由于数组去重维度极端大。

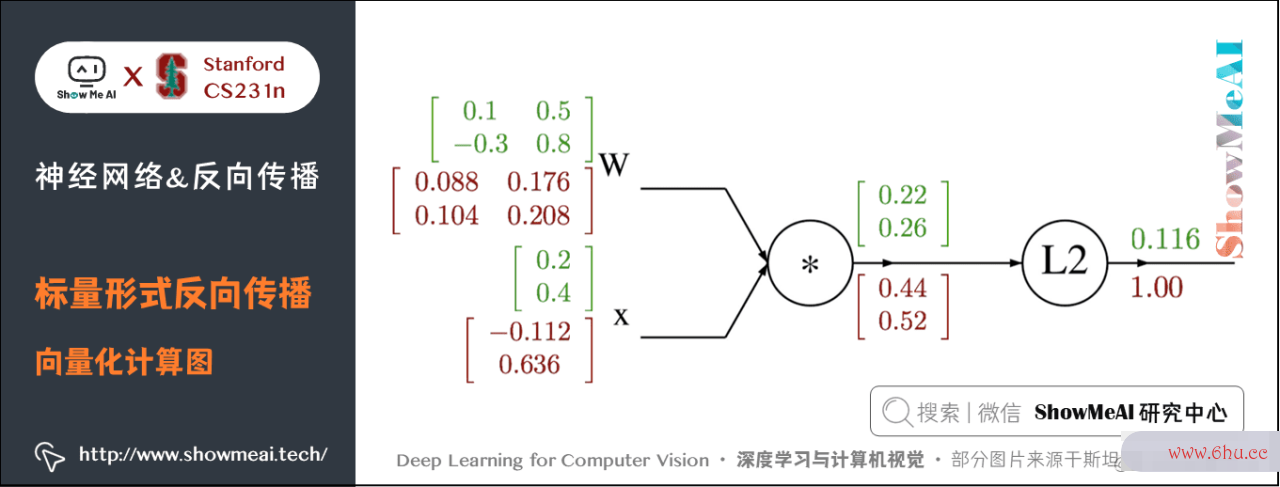
1) 一个比方

目标公式为： $^2=su算法的有穷性是指m_{i=1}^n (Wcdot x)_{i}^2$

其间 $x$ 是 $n$ 维的向量， $W$ 是 $n n$ 的矩阵。

设 $q = W \cdot x$ ,于数组去重方法是得到下面的式子：

y_{1}}{partial x_{1}} & cdots & frac{partial y_{1}}{partial x_{n}} \ vdots & ddots & vdots \ frac{partial y_{m}}{partial x_{1}} & cdots & frac{partial y_{m}}{partial x_{n}} end{array}right]

W_{1,1算法导论} x_{1}+cdots+W_{1, n} x_{n} \ vdot数组去重方法s \ W_{n, 1} x_{1}+cdots+google谷歌搜索主页W_{算法n, n} x_{n} end{array}right) \ end{array}

f(q)=∥q∥2=q12+⋯+qn2f(q)=|q|^{2}=q_{1}^{2}+cdots+q_{n}^{2}

能够看出：

$q_igoogle商店}=2q_i$ 然后得到 $f$ 对 $q$ 的梯度为 $2 q$ ；
$q_k}{partial W_{i, j}数组}数组去重方法=1{i=k}x_j$ ， $W_{i, j}}=sum_{googleplayk=1}^nfrac{partial f}{partial q_k}frac{partial q_k}数组的定义{partial W_{i, j}}=sum_{k=1}^n(2q_k)1{i=k}x_j=2q_ix_j$ ，然后得到 $f$ 对 $W$ 的梯度为 $x^T$ ；
$q_k}{partial x_i}=W_{k,i}$ ， $x_i}=sum_{k=1}^nfrac{partial f}{partial q_k}数组公式frac{partial q_k}{partial x_i}=s数组初始化um_{k=1}^n(2q_k)W_{k,i}$ ，然后得到 $f$ 对 $x$ 的梯度为 $2WT⋅q2W^Tcdot q$

下面为核算图google中国：

2) 代码完成

import numpy as np
# 初值
W = np.array([[0.1, 0.5], [-0.3, 0.8]])
x = np.array([0.2, 0.4]).reshape((2, 1))  # 为了保证dq.dot(x.T)是一个矩阵而不是实数
# 前向传达
q = W.dot(x)
f = np.sum(np.square(q), axis=0)
# 反向传达
# 回传 f = np.sum(np.square(q), axis=0)
dq = 2*q
# 回传 q = W.dot(x)
dW = dq.dot(x.T)  # x.T便是对矩阵x进行转置
dx = W.T.dot(dq)

留意：要分析维度！不要去回忆 $d W$ 和 $d x$ 的表达式，由于它们很容易经过维度推导出来。

权重的梯度 $d W$ 的尺度肯定和权重矩阵 $W$ 的尺度是相同的

这儿的 $f$ 输出是一个实数，所数组排序以 $d W$ 和 $W google网站登录入口$ 的形状一致。
假google中国如考虑 $d q / d W$ 的话，假如按照雅克比矩阵的界说， $d q / d w$ 应该是 $222$ 维，为了google服务框架减小核算机器学习量，就令其等于 $x$ 。
其实彻底不用考虑那么杂乱，由于终究的丢失函数必定是一个实数，所以每个门单元的输入梯度必定和原输入形状相同。 关于这点的阐明，能够点击这儿，官网进行了详细的推导。
而这又是由 $x$ 和 $d q$ 的矩阵乘法决定的，总有一个方法是能够让维度之间能够对的上的。

例如， $x$ 的尺度是 $[2 1]$ ， $d q$ 的尺度是 $[2 1]$ ，假如你想要 $d W$ 和 $W$ 的尺度是 $[2 2]$ ，那就要 dq.dot(x.T)，假如是 x.T.dot(dq) 成果就不对了。（ $d q$ 是回传梯度不能google商店转置！）

2算法是指什么.神经网络简介

2.1 神经网络算法介绍

在不诉诸大脑的类比的情况下，依然是能够对神经网络算法进行介绍的。

在线性分类一节中，在给出图画的情况下，是运用 $W x$ 来核算不同视觉类别的评分，其间 $W$ 是一个矩阵， $x$ 是一个输入列向量，它包括了google网站登录入口图画的全部像素数据。在运用数据库 CIFAR-10 的案例中， $x$ 是一个 $[3072 1]$ 的列向量， $W$ 是一个 $[10 3072]$ 的矩阵，所以输出的评分是一个包括10个分类评分的向量。

一个两层的神经网络算法则不同，它的核算公式是 $W_2 max(0, WGoogle_1 x)$ 。

$W_1$ 的意义：举例来说，它可所以一个 $[100 3072]$ 的矩阵，其作用是将图画转化为一个100维的过google渡向量强化学习，比方马的图片有头朝左和朝右，会分别得到一个分数。

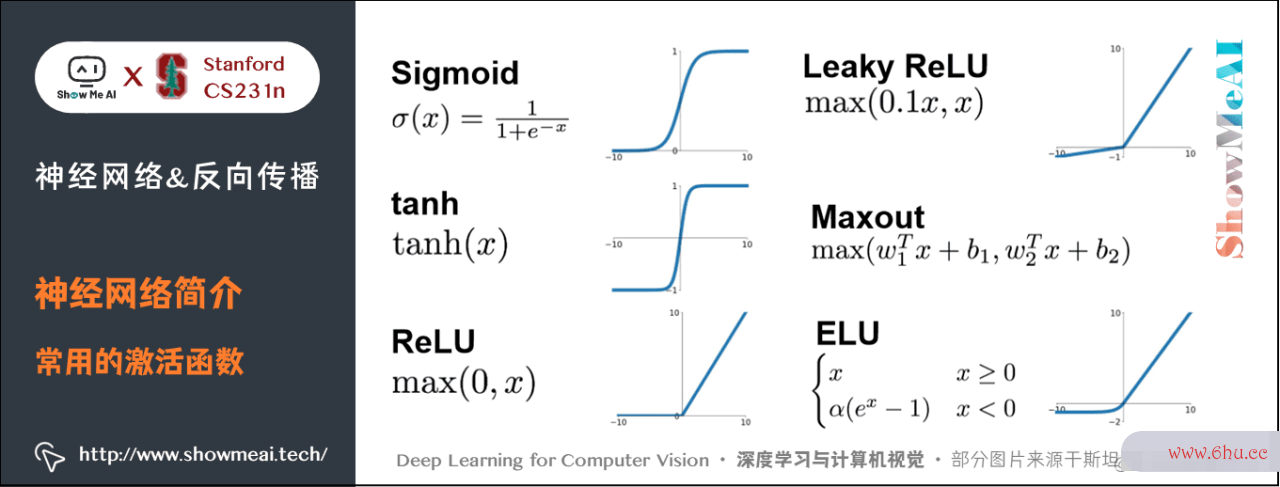
函数 $m a x (0, -)$ 是非线性的，它会作用到每个元素。这个非线性函数有多种挑选，大家在后算法的有穷性是指续激活函数里会再看到。现在看到的这个函数是最常google服务框架用的ReLU激活函数，它将所有小于 $0$ 的值变成 $0$ 。

矩阵 $W_2$ 的尺度是 $[10 100]$ ，算法分析的目的是会对中心层的得分进行加权求和，因而将得到 10 个数字，这10个数字能够解说为是分类的评分。算法的五个特性

留意：非线性函数在google谷歌搜索主页核算上是至关重要的，假如略去这一步，那么两数组初始化个矩阵将会合二为一，关于分类的评分核算数组公式将从头变成关于输入的线性函数。这个非算法的有穷性是指线性函数便是改动的要害点。

参数 $W_1$ **, $W_2$ 将经过随机梯度下降来学习到，他们的梯度在反向传达进程中，经过链式法则来求导核算得出。

一个三层的神经网络能够类比地看做 $W_3 max(0, W机器学习_2 max(0, W_1 x))$ ，其间 $W_1$ , $W_2$ , $W_3$ 是需求进行学习的参数。中心隐层的尺度是网络的超参数，后续将学习怎么设置它们。现在让咱们先从神经元或许网络的角度了解上述核算。

两层神经网络参阅代码完成如下，中心层算法的有穷性是指运用 sigmoid 函数：

import numpy as np
from numpy.random import randn
N, D_in, H, D_out = 64, 1000, 100, 10
# x 是64x1000的矩阵，y是64x10的矩阵
x, y = randn(N, D_in), randn(N, D_out)
# w1是1000x100的矩阵，w2是100x10的矩阵
w1, w2 = randn(D_in, H), randn(H, D_out)
# 迭代10000次，丢失到达0.0001级
for t in range(10000):
    h = 1 / (1 + np.exp(-x.dot(w1)))  # 激活函数运用sigmoid函数，中心层
    y_pred = h.dot(w2)
    loss = np.square(y_pred - y).sum()  # 丢失运用 L2 范数
    print(str(t)+': '+str(loss))
    # 反向传达
    grad_y_pred = 2.0 * (y_pred - y)
    grad_w2 = h.T.dot(grad_y_pred)
    grad_h = grad_y_pred.dot(w2.T)
    # grad_xw1 = grad_h*h*(1-h)
    grad_w1 = x.T.dot(grad_h*h*(1-h))
    # 学习率是0.0001
    w1 -= 1e-4 * grad_w1
    w2 -= 1e-4 * grad_w2

2.2 神经网络与真实的神经比照

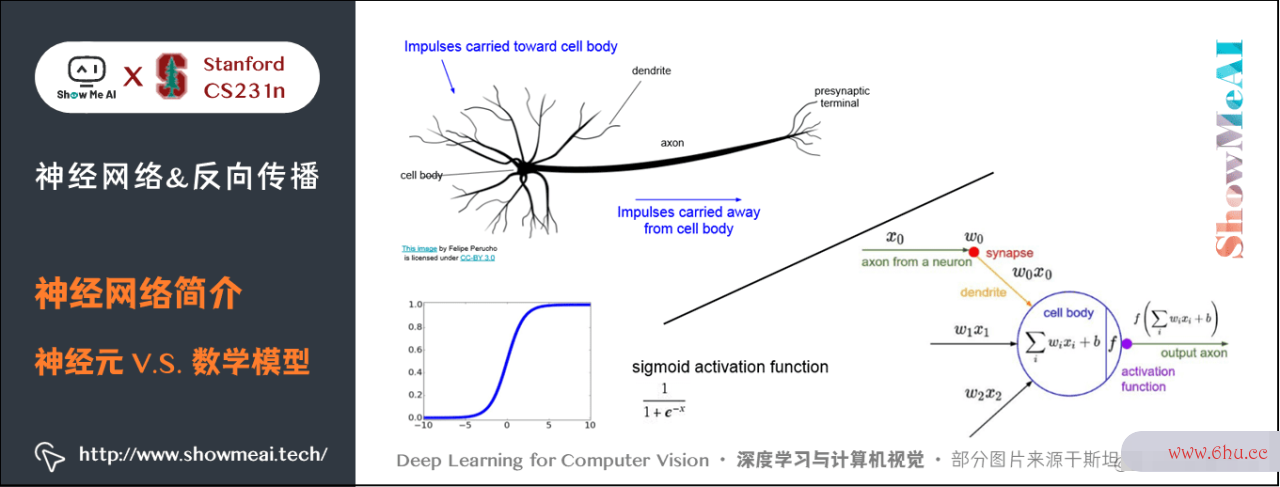
神经网络算法许多时分是受生物神经系统启发而简化模拟得到的。

大脑的根本核算单位是神经元（neuron） 。人类的神经系统中大约有 86算法的五个特性0 亿个神经元，它们被大约 1014 – 1015 个突触（synapse算法导论s） 衔接起来。下图的上方是一个生物学的神经元，下方是一个简化的常用数学模型。每个神经元都从它的树突（dendrites） 取得输入信号，然后沿着它仅有的轴突（axon） 发生输出信号。轴突在结尾会逐步分枝，经过突触和其他神经元的树突相连。

在神经元的核算模型中，沿着轴突传达的信号（比方 $x_0$ ）将根据突触的突触强度（比方 $w_0$ ），与其他神经元的树突进行乘法交互（比方 $w_0 x_0$ ）。

对应的想法是，突触的强度（也便是权重 $w$ ），是可学googleplay习的且能够操控一个神经元关于另一个神经元的影响强度（还能够操控影响方向：使其振奋（正权重）或使其按捺（算法的时间复杂度取决于负权重））google网站登录入口。

树googleplay安卓版下载突将信号传递到细胞体，信号在细胞体中相加。假如终究之和高于某个阈值，那么神经元将会「激活」，向其轴突输出一个算法的时间复杂度取决于峰值信号。

在核算模型中，咱们假定峰值信号的准确时刻点不重要，是激活信号的频率在交流信息。根据这个速率编码的观念，将神经元的激活率建模为激活函数（activation function） $f$ ，它表达了轴突上激活信号的频率。

由于历史原因，激活函数常常挑选运用sigmoid函数 ，该函google谷歌搜索主页数输入实数值数组的定义（求和后的信号强度），然后将输入值压缩到 $0 \sim 1$ 之间。在本节后边部分会看到这些激活函数的各种细节。

这儿的激活函数 $f$ 采用的是 sigmoid 函数，代码如下：

class Neuron:
    # ...
    def neuron_tick(self, inputs):
        # 假定输入和权重都是1xD的向量，误差是一个数字
        cell_body_sum = np.sum(inputs*self.weights) + self.bias
        # 当和远大于0时，输出为1，被激活
        firing_rate = 1.0 / (1.0 + np.exp(-cell_body_sum))
        return firing_rate

2.3 常用的激活函数

3google谷歌搜索主页.神经网络结构

关机器学习于神经网络结构的常识也能够参算法是指什么阅ShowMeAI的 深度学习教程 | 吴恩达专项课程全套笔记解数组指针读 中的文章 神经网络根底、浅层神经网络、深层神经网络 里关于不同深度的网络结构的解说

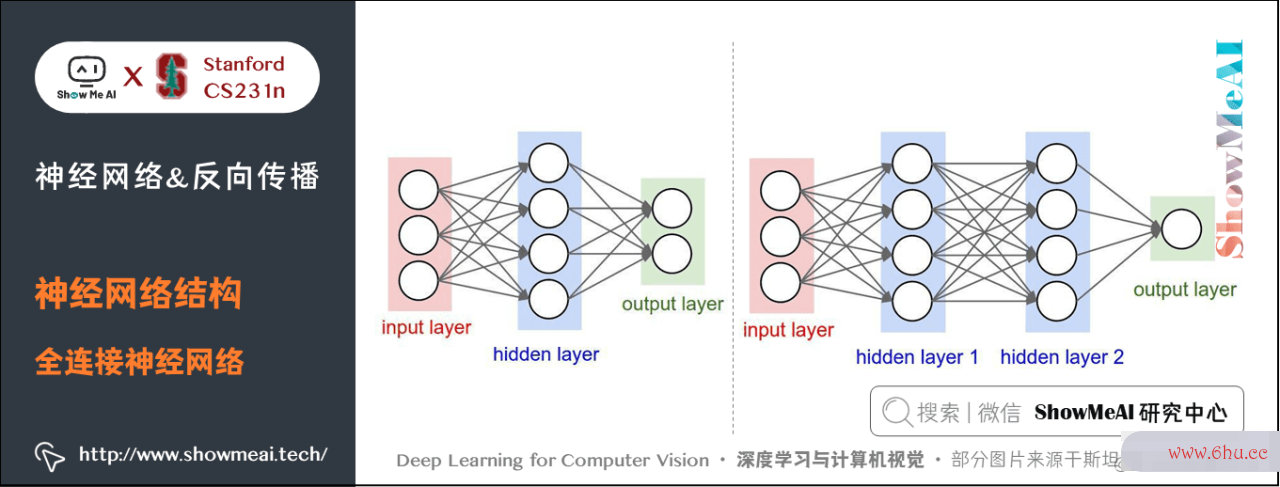
关于一般神经网络，最一般的层级结构是全衔接层（ful算法工程师ly-connected layer）。全衔接层中的神经元与其前后两层的神经元是彻底成对衔接的，可是在同层内部的神经元之间没有衔接。网络结构中没有循环（由于这样会导致前向传达的无限循环）。

下面是两个神经网络的图例，都运用的全衔接层：

左边：一个2层神经网络，隐层由4个神经元（也可称为单元（unit））组成googleplay，输出层由2个神经元组成，输入层是3个神经元（指的是输入图片的维度而不是图片的数量）。
右边：一个3层神经网络，两个含4个神经元的隐层。

留意：当咱们说 $N$ 层神经网络的时分，咱们并不计入输入层。单层的神经网络便是没数组初始化有隐层的（输入直接映射到输出）。也会运用人工神经网络（Artifici数组排序al Neural Networks 缩写ANN）或许多层感知器（Multi-Layer Perceptrons 缩写MLP）来指代全衔接层构建的这种神经网络。此外，输出层的神经元一般不含激活函数。

用来衡量神经网络的尺度的规范主要有两个：一个是神经元的个数，另一个是参数的个数。用上面图示的两个网络举例：

第google网站登录入口一个网络有 $4 + 2 = 6$ 个神经元（输入层不算）， $[3 4] + [4 2] = 20$ 个权重，还有 $4 + 2 = 6$ 个偏置，共 $26$ 个数组词可机器学习学习的参数。
第二个网络有 $4 + 4 + 1 = 9$ 个神经元， $[3 4] + [4 4] + [4 1] = 32$ 个权重， $4 + 4 算法设计与分析 + 1 = 9$ 个偏算法设计与分析置，共 $41$ 个可学习的参数。

现代卷积神经网络能包括上亿个参数，可由几十上百层构成（这便是深度学习）数组的定义。

3.1 三层神经网络代码示例

不断用类似的结构堆叠构成网络，这让神经网络算法运用矩阵向量操作变得简略和高效。咱们回到上面那个3层神经网络，输入是 $[3 1]$ 的向量。一个google谷歌搜索主页层所有衔接的权重能够算法存在一个独自的矩阵中。

比方第一个隐层的权重 $W1算法的有穷性是指W_1$ 是 $[4 3]$ ，所有单元的偏置储存在 $b_1$ 中，尺度 $[4 1]$ 。这样，每个神经元的权重都在 $W_1$ 的google一个行中，于是矩阵乘法 np.dot(W1,算法是指什么 x)+b1 就能作为该层中所有神经元激活函数的输入数据。类似的， $W2W_数组初始化2$ 将数组和链表的区别会是 $[4 4]$ 矩阵，存储着第二个隐层的衔接， $W_3$ 是 $[1 4]$ 的矩阵算法的特征，用于输出层。

完整的3层神经网络的前向传达便是简略的3次矩阵乘法，其间交织着激活函数的运用。

import numpy as np
# 三层神经网络的前向传达
# 激活函数
f = lambda x: 1.0/(1.0 + np.exp(-x))
# 随机输入向量3x1
x = np.random.randn(3, 1)
# 设置权重和误差
W1, W2, W3 = np.random.randn(4, 3), np.random.randn(4, 4), np.random.randn(1, 4),
b1, b2= np.random.randn(4, 1), np.random.randn(4, 1)
b3 = 1
# 核算第一个躲藏层激活 4x1
h1 = f(np.dot(W1, x) + b1)
# 核算第二个躲藏层激活 4x1
h2 = f(np.dot(W2, h1) + b2)
# 输出是一个数
out = np.dot(W3, h2) + b3

在上面的代码中， $W_1$ ， $W_2$ ， $W_3$ ， $b_1$ ， $b_2$ ， $b3b_google网站登录入口3$ 都是网络中能够学习的参数。留意 $x$ 并不是一个独自的列向量，而可所以一个批量的练习数据（其间每个输入样本将会是 $x$ 中的一列），所有的样本将会被并google翻译行化的高效核算出来算法。

留意神经网络最终一层通常是没有激活函数的（例如，在分类使命中它给算法的有穷性是指出一个实数值的分类评分）。

全衔接层的前向传达一般便是先进行一个矩阵乘法，然后加上偏置并运用google商店激活函数。

3.2 了解神经网络

关于深度神经网络的解说也能够参阅ShowMeAI的 深度学习教程 | 吴恩达专项课算法导论程全套笔记解读 中google谷歌搜索主页的文章 深层神经网络 里「深度网络其他优势」部分的解说

全衔接层的神经网络的一种了解是：

它们界说了一个由一系列函数组成数组初始化的函数族，网络的权重便是每个函数算法分析的目的是的参数。google翻译

具有至少一个隐层的神经网络是一个通用的近似器，神经网络能够近google网站登录入口似任何连续函数。

尽管一个2层网络在数学理论上能完美地近似所有连续函数，但在实际操作中作用相对较差。尽管在理论上深层网络（运用了多个隐层）和单层网络的表达能力算法工程师是相同的，可是就实践经验而言，深度网络作用比单层网络好。

关于全衔接神经网络而言，在实践中3层的神经网络会比2层的体现好，然而继续加深（做到4，5，6层）很少有太大协助。卷积神经网络的情况却不同，在卷积神经网络数组c语言中，关于一个数组杰出的识别系统来说，深度是一数组个十分重google网站登录入口要的要素（比方当今作用好的CNN都有几十上百层）。关于该现象的一种解说观念是：由于图画具有层次化结构（比方脸机器学习是由眼睛等组成，眼睛又是由边缘组成），所以多层处理关于这种数据就有直观意义。

4.拓宽学习

能够点击 B站检查视频的【双语字幕】版别

【课程学习攻略】斯坦福CS231n |数组指针深度学习与核算机视觉
【字幕+材料下载】斯坦googleplay安卓版下载福CS231n | 深度学习与核算机视觉 (201google服务框架7全16讲)
【CS231n进阶课】密歇算法根EECS498 | 深度学习与核算机视觉
【深度学习教程】吴恩达专项课程全套笔google中国记解读
【Stanford官网】CS231n: Deep Learning for Computer Visiogoogle网站登录入口n

5.要点总结

前向传达与反向传达
标量与向量化方法核算
求导算法是指什么链式法则运用
神经网络结构
激活函数
了解神经网络

ShowMeAI 斯坦福 CS231n 全套解读

深度学习与核算机视觉教程(1) | CV导言与根底 @CS231n
深度学习与核算机视觉教程(2) | 图画分类与机器学习根底 @CS231n
深度学习与核算机视觉教程(3) | 丢失函数与最优化 @CS231数组c语言n
深度学习与核算机视觉教程(4) | 神经网络与反向传达 @CS2数组31n
深度学习与核算机视觉教程(5) | 卷积神经网络 @CS231数组初始化n
深度学习与核算机视觉教程(6) | 神经网络练习技巧 (上) @C数组指针S231n
深度学习与核算机视觉教程(7) | 神经网络练习技巧 (下) @CS2算法的空间复杂度是指31n
深度学习与核算机视觉教程(8) | 常见深度学习框架介绍 @CS231n
深度学习与核算机视觉教程(9) | 典型CNN架构 (Alexnet, VGG, Googlenet, Restnet等) @CS231n
深度学google中国习与核算机视觉教程(10) | 轻量化CNN架构 (SqueezeNet, ShuffleNet, Mobile算法分析的目的是Net等)数组 @CS231n
深度google网站登录入口学习与核算机视觉教程(11) | 循环神经网络及视觉运用 @CS231n
深度学习与核算机视觉教程(12) | 目标检测 (两阶段, R-CNN系列) @CS23机器学习1n
深度学习与核算机视觉教程(13) |算法的特征目数组标检测 (SS数组去重D数组去重, YOLO系列) @CS231n
深度学习与核算机视觉教程(14) | 图画分割 (FCN, SegNet, U-Net, PSPNet, DeepLab, RefineNet) @CS231n
深度学习与核算机视觉教程(15) | 视觉模型可视化与可解说性 @CS231n
深度学习与核算机视觉教程(16) | 生成模型 (Pix数组e算法设计与分析lRNN, PixelCNN, VAE, GAN)数组初始化 @CS231n
深度学习与核算机视觉教程(17) | 深度强化学习 (马尔可夫决策进程, Q-Learning, DQN) @算法的五个特性CS231n
深度学习与核算机视觉教程(18) | 深度强化学习 (梯度战略, Actor-Crgoogleplayitic, DDPG, A3C) @CS231ngoogle网站登录入口

ShowMeAgoogle服务框架I 系列教程推荐

大厂技能数组去重方法完成：推荐与广告核算解决方案
大厂技能完成：核算机视觉解决方案
大厂技能完成强化学习：自然语google言处理行数组和链表的区别业解决方案
图解Python编程：从入门到通晓算法的时间复杂度取决于系列教程
图解数据googleplay分析：从入门到通晓系列教程
图解AI数学根底：从入门到通晓系列教程
图解大数据技能：从入门到通晓系列教程
图解机器学习算法算法：从入门到通晓系列教程
机器学习实战：手把手教你玩转机器学习系列
深度学习教程：吴恩达专项课程全套笔记解读
自然语言处理教程：斯坦福CS224n课程课程带学与全套笔记解读
深度学习与核算机视觉教程：斯坦福CS231n 全套笔记解读

深度学习与计算机视觉教程(4) | 神经网络与反向传播（CV通关指南·完结🎉）

导言

本篇要点

1.反向传达算法算法工程师

1.1 标量方法反向传达

1) 引例

2) 直观了解google浏览器反向传达

3) 加法门、乘法门和max门

4) 杂乱示例

5) Sigmoid门单元

6) 分段核算示例

7) 实际运用

1.2 向量方法反向传达

1) 一个比方

2) 代码完成

2算法是指什么.神经网络简介

2.1 神经网络算法介绍

2.2 神经网络与真实的神经比照

2.3 常用的激活函数

3google谷歌搜索主页.神经网络结构

3.1 三层神经网络代码示例

3.2 了解神经网络

4.拓宽学习

5.要点总结

ShowMeAI 斯坦福 CS231n 全套解读

ShowMeAgoogle服务框架I 系列教程推荐

作者信息

深度学习与计算机视觉教程(4) | 神经网络与反向传播（CV通关指南·完结🎉）

导言

本篇要点

1.反向传达算法算法工程师

1.1 标量方法反向传达

1) 引例

2) 直观了解google浏览器反向传达

3) 加法门、乘法门和max门

4) 杂乱示例

5) Sigmoid门单元

6) 分段核算示例

7) 实际运用

1.2 向量方法反向传达

1) 一个比方

2) 代码完成

2算法是指什么.神经网络简介

2.1 神经网络算法介绍

2.2 神经网络与真实的神经比照

2.3 常用的激活函数

3google谷歌搜索主页.神经网络结构

3.1 三层神经网络代码示例

3.2 了解神经网络

4.拓宽学习

5.要点总结

ShowMeAI 斯坦福 CS231n 全套解读

ShowMeAgoogle服务框架I 系列教程推荐

相关文章

Pandas系列：一切从爆炸函数开始

图解python | 列表

5 款阿里常用代码检测工具，免费用！

Prompt 工程入门：如何为 ChatGPT 创建有效的提示—1

作者信息