一起养成写作习惯！这是我参与「日新计划 4 月更文挑战」的第27天，点击查看活动详情。

前言

本文为我之前在CSDN平台上的一篇博客记录。原链接为：blog.csdn.net神经网络/u011426236/…

Pytorch中的mini-ba数组公式tch和优化器

本篇笔记主要对应于莫凡Pytorch中的3.5和3.6节。主要讲了如何使用Pytorch中的mini-batch和优化器。

Pytorch中的mini-batch

在笔记笔记本电脑排名前十二、三中搭建的网络中，我们是一次性直接将整个训练集送进网络，这种方式称为Full Batch Learning。但是当数据量很大时，首先一次性加载这么多数据收到了内存的限制，同时由于要计数组初始化算每个样例的梯度，计算速度也会下降。

那么我们是数组去重否可python是什么意思以每次只python编程用一条样例数据进行训练呢。答案是可以的，但是这样每次的随机性太大，这种方法称为随机梯度下降法。这种方法永远不会收敛，而是会一直在最小值附近波动。

所以，取一个折中的做法是选取一个合理的batch_size大小进行训练，每次从整个训笔记本练集中拿出一部分来训练。

这里我们数组指针简单展示线程数越多越好吗Pytorch中的mini-batch操作如何进行。首先我们需要导入Data模块

import torch
import torch.utils.data as Data

设置超参数BATCH_SIZE

BATCH_SIZE = 8

生成训练数据，这里直接生成了10个整数作为训练数据。

x = torch.linspace(1, 10, 10)
y = torch.linspace(10, 1, 10)

接下来，我们进行batch的一些设置

torch_dataset = Data.TensorDataset(x, y)
loader = Data.DataLoader(
    dataset = torch_dataset,    # 要划分的数据集
    batch_size = BATCH_SIZE,    # 所设置的batch大小，一般2的次方倍会有助于快速计算
    shuffle = True,             # 是否打乱，打乱更有助于训练
    num_workers = 2,            # 所使用的线程数目
)

使用mini-batch的展示，这里当最后一个分组不够时，会只用剩下的那些神经网络对信息的存储依赖什么。

Epoch:  0 | Step:  0 | batch x:  [ 9. 10.  8.  3.  5.  6.  1.  4.] | batch y:  [ 2.  1.  3.  8.  6.  5. 10.  7.]
Epoch:  0 | Step:  1 | batch x:  [7. 2.] | batch y:  [4. 9.]
Epoch:  1 | Step:  0 | batch x:  [3. 7. 2. 8. 4. 1. 6. 5.] | batch y:  [ 8.  4.  9.  3.  7. 10.  5.  6.]
Epoch:  1 | Step:  1 | batch x:  [ 9. 10.] | batch y:  [2. 1.]
Epoch:  2 | Step:  0 | batch x:  [4. 5. 8. 7. 2. 1. 3. 6.] | batch y:  [ 7.  6.  3.  4.  9. 10.  8.  5.]
Epoch:  2 | Step:  1 | batch x:  [ 9. 10.] | batch y:  [2. 1.]

比如上面所展示的，在epoch 0，由于设置的batch=8，所以第一个step取了8个example，即x=[9.10.8.3.5.6.1.4.],y=[2.1.3.8.6.5.10.7.]x=[9. 10. 8. 3. 5. 6. 1. 4.], y=[ 2. 1. 3. 8. 6. 5. 10. 7.]。而在第二个step，由于只剩下2个example没有被取到，而2<82<8，故第二个step直接将剩下的example取出。

不同优化器的对比

我们对比几种不同的优化器性能。这里主要对比四种不同的优化器：

  • SGD（随机梯度下降）
  • Momentum（动量梯度下降线程数越多越好吗）
  • RMSprop（root mepython怎么读an square）
  • Adam（Adaptive Moment Estimation）

首先，我们导入相关的库和设置超参数

import torch
import torch.utils.data as Data
import torch.nn.functional as F
import matplotlib.pyplot as plt

这里学习率设置为0.01，Batch线程池的七个参数_size设置为32，设置12个Epoch。

LR = 0.01
BATCH_SIZE = 32
EPOCH = 12

接着我们生成和展示训练数据

x = torch.unsqueeze(torch.linspace(-1, 1, 1000), dim=1)
y = x.pow(2) + 0.1 * torch.normal(torch.zeros(*x.size()))
# plot dataset
plt.scatter(x.numpy(), y.numpy())
plt.show()

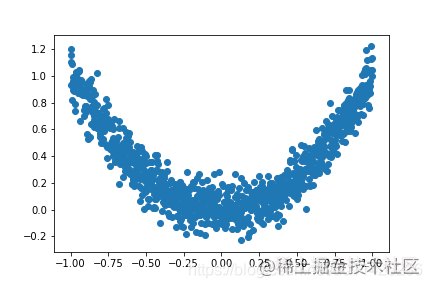
训练数据的可视化展示效果如下，即一个带有噪声干扰的二次函数形式的分布：

莫凡Pytorch教程（六）：Pytorch中的mini-batch和优化器

然后，我们使用mini-batch进行数据集划分

torch_dataset = Data.TensorDataset(x, y)
loader = Data.DataLoader(
    dataset=torch_dataset,
    batch_size=BATCH_SIZE,
    shuffle=True,
    num_workers=2
)

并搭建网笔记本电脑开不了机络

# default network
class Net(torch.nn.Module):
    def __init__(self, n_feature, n_hidden, n_prediction):
        super(Net, self).__init__()
        self.hidden = torch.nn.Linear(n_feature, n_hidden)
        self.prediction = torch.nn.Linear(n_hidden, n_prediction)
    def forward(self, x):
        x = F.relu(self.hidden(x))
        y = self.prediction(x)
        return y

接着，我们生成使用不同优化器的网络

# different nets
net_SGD = Net(1, 20, 1)
net_Momentum = Net(1, 20, 1)
net_RMSprop = Net(1, 20, 1)
net_Adam = Net(1, 20, 1)
nets = [net_SGD, net_Momentum, net_RMSprop, net_Adam]

以及不同的优化器，这里优神经网络英文化器都是来自于torch.optim库，可以直接调用

opt_SGD = torch.optim.SGD(net_SGD.parameters(), lr=LR)
opt_Momentum = torch.optim.SGD(net_Momentum.parameters(), lr=LR, momentum=0.8)
opt_RMSprop = torch.optim.RMSprop(net_RMSprop.parameters(), lr=LR, alpha=0.9)
opt_Adam = torch.optim.Adam(net_Adam.parameters(), lr=LR, betas=(0.9, 0.99))
optimizers = [opt_SGD, opt_Momentum, opt_RMSprop, opt_Adam]

我们设置损失函数为最小均方误差函数MSE，使用一个数组来记录lospython语言s的变化情况，方便后续展示。

loss_func = torch.nn.MSELoss()
losses_his = [[], [], [], []]   # record loss

最后，进行训练输出中间结果

for epoch in range(EPOCH):
    print("epoch: ", epoch)
    for step, (batch_x, batch_y) in enumerate(loader):
        b_x = Variable(batch_x)
        b_y = Variable(batch_y)
        for net, opt, l_his in zip(nets, optimizers, losses_his):
            output = net(b_x)               # get output for every net
            loss = loss_func(output, b_y)   # compute loss for every net
            opt.zero_grad()                 # clear gradients for next train
            loss.backward()                 # backpropagation, compute gradients
            opt.step()                      # apply gradients
            l_his.append(loss.data)      # loss recorder
labels = ['SGD', 'Momentum', 'RMSprop', 'Adam']
for i, l_his in enumerate(losses_his):
    plt.plot(l_his, label=labels[i])
plt.legend(loc='best')
plt.xlabel('Steps')
plt.ylabel('Loss')
plt.ylim((0, 0.2))
plt.show()

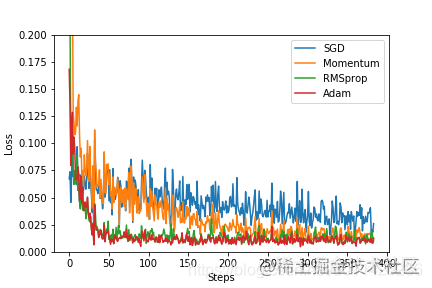
最后，得到的展示输出如下：

莫凡Pytorch教程（六）：Pytorch中的mini-batch和优化器

这里横坐标为训练的step，纵坐标为模型的loss值。可以看到，随python安装教程着训练的进行，使用Adam和RMSprop效果l笔记本oss的下降情况相仿，最好。而使用最简单的SGD后loss的下降情况效果最差，不过这一情形再加入动量后有所改善。

参考

  1. 莫凡Python：Pytorch动态神经网络，mofanpy.com/tutorials/m…